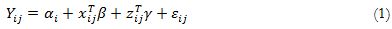
ARTICLES
Differences in Motivations and Academic Achievement
Diferencias en las motivaciones y el rendimiento académico
Les différences dans les motivations et la réussite scolaire
Luis Fernando Gamboa1; Mauricio Rodríguez Acosta*; Andrés García-Suaza**
1 Departamento de Economía, Universidad del Rosario, Bogotá. Address: Department of Economics, Universidad del Rosario, Calle 14 No 4-69, Bogotá, Colombia. Phone: +(571)-2970200 X 8013. E-mail: luis.gamboa@urosario.edu.co.
* CentER – Department of Economics, Tilburg University, Tilburg, Netherlands. Address: CentER - Department of Economics, Tilburg School of Economics and Management, Tilburg University P.O. Box 90153, 5000 LE Tilburg, The Netherlands. Phone: +31-(0)13-4668758. E-mail: M.A.Rodriguez@tilburguniversity.edu.
** Department of Economics, Universidad del Rosario - Universidad Carlos III, Bogotá. Address: Department of Economics, Universidad del Rosario, Calle 14 No 4-69, Bogotá, Colombia. Student MSc Economics, Universidad Carlos III. E-mail: andres.garcia@urosario.edu.co.
–Introduction. –I. Background. –II. Empirical Strategy. –III. Data. –IV. Results. – Concluding Remarks. –References
Primera versión recibida el 4 de febrero de 2013; versión final aceptada 22 de marzo de 2013
ABSTRACT
This paper provides new evidence on the effect of pupils' self-motivation on academic achievement in science across countries. By using the OECD's Programme for International Student Assessment 2006 (PISA 2006) test, we find that self-motivation has a positive effect on students' performance. Instrumental Variables Quantile Regression is used to analyze the existence of different estimated coefficients over the scores distribution, allowing us to deal with the potential endogeneity of self-motivation. We find that the impact of intrinsic motivation on academic performance depends on the pupil's score. Our findings support the importance of designing focalized programs for different populations that foster their motivation towards learning.
Keywords: intrinsic motivations, education, ICTs, science.
JEL classification: C36, D83, I21.RESUMEN
Resumen: Este documento presenta nueva evidencia sobre el efecto de la motivación de los estudiantes en el rendimiento académico. Utilizando la información del examen realizado por el Programa para la Evaluación Internacional de Alumnos de la OCDE en 2006 (PISA 2006), se encuentra que la motivación tiene un efecto positivo sobre el rendimiento de los estudiantes. Para esto, se recurre a la metodología de regresión cuantílica con variables instrumentales, la cual permite estimar diferentes coeficientes para las variables explicativas a lo largo de la distribución de puntajes en el examen y corregir por la posible endogeneidad de la motivación. Dado que el efecto de la motivación depende del puntaje de los estudiantes, nuestros resultados resaltan la importancia de diseñar políticas que promuevan la motivación focalizadas en función del rendimiento académico.
Palabras clave: motivaciones intrínsecas, educación, TICs, ciencia
Clasificación JEL: C36, D83, I21.RÉSUMÉ
Cet article présente des nouveaux résultats concernant l'effet de la motivation des élèves dans leur réussite scolaire, à partir des données disponibles dans l'examen effectué par le Programme for International Student Assessment de l'OCDE en 2006 (PISA 2006). Les résultats montrent que la motivation a un effet positif sur la réussite scolaire. Pour ce faire, nous utilisons la méthode des variables instrumentales de régression quantile, ce qui nous a permis d'estimer les différents coefficients pour les variables explicatives, tout au long de la distribution des scores dans l'examen, et corriger ainsi l'endogénéité possible de la variable motivation. Etant donne le fait que la motivation dépend des scores dans un examen, nos résultats soulignent l'importance de concevoir des politiques qui favorisent la motivation axée sur la réussite scolaire.
Mots-clés: motivation intrinsèque, éducation, TICs, science.
JEL Classification: C36, D83, I21.
Introduction
The societal benefits from increasing the added value of education are rather undisputable. All the agents involved in the design of educational systems are in a continuous quest for mechanisms to improve the effectiveness of educational inputs and their complementarity. In this regard, it is fundamental to acknowledge that learning is a complex process in which both motivations and inputs play a significant role. The set of aspects belonging to the definition of motivation includes interest, goals, and external enticements. Then the effectiveness of public educational policies should take into account the motivational dimension as well as the fact that its impact depends on the age of pupils and on their schooling level.
The purpose of this document is to provide new evidence on the effect of motivation on academic achievement in sciences. The role of motivation in academic achievement is still controversial because of its measurement. Academic achievement is a goal for teachers and students. Students' behavior in school is a function of their effort and the expected reward from learning. The effort associated to learning has a lower cost when the goals correspond to motivated students.
Educational outcomes result from a combination of educational inputs using specific technologies (Coleman et al. 1966). These inputs have higher effect on educational outcomes when students have better incentives to study. Motivation reduces the disutility of effort and may cause that students devote more time to education. Moreover, motivation could positively affect educational outcomes by at least two different channels. First, greater motivation is directly related to students' effort: attendance, discipline, time devoted to homework, among others (Betts 1996; Bishop et al. 2003; Cooper 1989). Second, it could increase the perceived utility from learning (Boissiere, knight & Sabot 1985; Bishop 1989; Bishop 1992; Bishop 2006).
Motivation has been traditionally studied in two distinct dimensions: extrinsic and intrinsic. They can be seen as parallel or sequential. In the early stages of education, external motivations could have higher effect. Note that during childhood, students often receive external rewards in exchange for their good performance. This is not necessarily the case with teenagers. In later stages, when students become more aware of the importance of knowledge, the role of internal motivations increases.
In this paper, we only explore the intrinsic component.2 Self-motivation and effort can be influenced by both parents and teachers. For instance, parents affect children's performance by providing them with economic resources and homework support. Furthermore, when parents take children's education as an investment, instead of as a consumption activity, they have a clear interest in the efficient use of schooling resources. Additionally, teachers influence students' motivation by means of external rewards (or 'threats') and their own performance (Bishop 1999).
The importance of inputs on academic outcomes has been traditionally studied using the Educational Production Function (EPF) approach. Under this framework, the effect of observable factors (physical capital, peer effects, etc.) on specific educational outcomes (final grades, drop-out rates, scores in tests) has been analyzed recognizing the existence of other unobservable aspects (e.g., ability). It is well-known that the existence of unobserved factors such as motivations and abilities might bias the estimated effects of the observable inputs on the students' achievement. In this paper, we focus on the effect of student's motivation using self-reported answers to try to overcome its unobservability.
We assume that intrinsic motivation is the best representation of the concept of self-motivation. That is, students are intrinsically motivated to work if the threat of negative external evaluation is not salient and when their goals do not depend on extrinsic reasons for completing tasks (Sharma 2010).
Furthermore, we concentrate on the relationship between motivation and achievement in science. Science is one of the fields where learning requires 'special pleasure for learning' and the importance of discipline and perseverance is crucial for being successful in this area. In contrast to the previous literature, our analysis is performed along the score's distribution.
The contribution of the paper is twofold. First, we provide new evidence about the role of motivation on students' achievement in an international comparative test. This task is achieved by constructing an index of self-motivation using data from the students' questionnaire included in the Programme for International Student Assessment 2006. PISA 2006 has better comparability and provides more accurate information about pupils' performance than school grades.3 Indeed, centralized examinations – which should make students' learning efforts more visible to external observers and wipe out students' incentives to lower the average performance level of the class – have been shown to have a positive impact on students' educational achievement. Our index allows us to control for the effect of motivation (an unobserved factor) in the EPF.
However, there may be an endogeneity problem. In order to address it, we use an instrumental variables approach. Since our definition of motivation and choice of instrument may still be subject to controversy, we also discuss the possible biases in our estimations.
The second contribution is methodological. We use Instrumental Variables Quantile Regression -IVQR- to estimate particular marginal effects by score quantile after controlling for country-level fixed effects (Powell 2009; Chernozhukov and Hansen 2008). This strategy can be used to provide a picture of the differences in the tails of the scores distribution. This approach is important for the analysis of the effectiveness of public programs designed to stimulate education, since the effect on the low tail might be more attractive from the policy perspective than the effect on the upper tail.
Our results indicate that self-motivation has a positive impact on school attainment, but its effect is different across the scores distribution after controlling for country-effects and other educational factors. In fact, the size of the coefficient is about twice in students with low performance as compared with those that perform the best. These results support the importance of designing focalized programs for different populations, mainly in developing countries where differences between the tails of the distributions tend to be considerable. However, our estimations might underestimate the final effect.
The paper is organized as follows. Section I presents some theoretical background on the determinants of school achievement. Section II is dedicated to the empirical strategy. Section III summarizes the structure of the database. Section IV presents the econometric exercises. And the last section is devoted to concluding remarks.
I. Background
Economic literature on the determinants of educational quality is growing since the contribution of Coleman et al. (1966). This literature includes inputs such as physical resources, budget, teachers, and institutions (see Al-Samarrai (2002) and the references therein) in the Educational Production Function (EPF). The relationship between students' test scores and a school's capital stock is neither unique nor robust (Hanushek 1998; Lee and Barro 2001; Fuchs and Woessmann 2008). It seems that other unobservable factors such as motivation may affect the final outcome achieved by students. Students' productivity in any task depends on their available resources and their effort, represented by their motivation. They can also use their motivation to provide better signaling for their teachers and parents. As a result, classroom interactions could provide variations in the effect of each variable because peers' motivation could induce modifications in individual behaviors. That is, teacher behavior and other characteristics within the classroom can be dependent on the composition of the group (e.g., gender, racial, or socioeconomic) (see, Eisenkopf, 2008).
Motivation is a complex concept close to preferences, attitudes, perseverance or interest's concepts. Walter and Hart (2009) define it as an individual's desire, power and tendency to act in a particular way. Koaler, Baumert and Shanabel (2001) treat interest equally as motivation. Motivation might be also understood as a result of an intrinsic and extrinsic process where individuals respond to internal as well as external rewards, teacher's praise, and positive feedback, among others (Deci et al. 1991). Hence, the effect of motivation on the quality of education could come from different perspectives. A non-exhaustive list includes: i) more motivated students see in learning an activity with a higher utility than leisure; ii) motivation increases the number of questions in the student and this induces her to look for answers, and iii) motivation generates a positive externality, when students value the subjects they are studying (Bishop 2007). Intrinsic motivation reduces the disutility of effort and provides effects other than external motivations in the student. Deci et al.(1999) state that tangible awards and prizes decrease intrinsic motivation when they are frequently used. Eisenberger et al. (1999) carried out a meta-analysis about the effects of rewards on intrinsic motivation and found similar results as Deci et al. (1999), but they also highlight the importance of the awards 'presentation' in the final effect.
As Lazear (2001) states, more homogeneity could be better for teachers' efficiency because time spent on things out of the schedule or the course program decreases instructor's productivity. In terms of motivation, peer effects could play an important role when they allow using a teacher's time in aspects related to incentivize learning and knowledge rather than in managing behavioral problems at the classroom. This aspect is not easy to solve with the available data because these are not representative at the school level.
Teachers and parents might affect motivation using different strategies under distinct environments. Parents could work hard on it by using verbal rewards or positive feedbacks and prizes. Their effectiveness is not clearly measured in the literature (Eisenberger, Rierce & Cameron, 1999). Teachers influence motivation from the first years of education in a more complex process. This comes from aspects such as the expected rate of return from their initiative and heterogeneity among their pupils. Given that parents invest economic resources and teachers invest time, the rate of return of each one can differ. Additionally, heterogeneity in motivation levels into the classroom should modify a teacher's strategies. When low motivation levels are translated to students' behavior, the effectiveness of teacher practices decreases. Hence, as Lazear (2001) notes, most of the teaching practices face negative externalities when the importance of well-behaved students is lower than their counterparts. Classrooms with high variance in effort and motivation levels can suffer from peer group pressures when disruptive classmates prevent the others from learning. In some cases, parents try to send their children to selected (private) schools preventing these behaviors (Bishop 2006).
In response to the academic results in the Third International Mathematics and Science Study (TIMMS), the educational process in the United States was revised by considering the importance of including the culture and interests of Hispanics and other immigrant communities (American Association for the Advancement of Science, AAAS 1989). Colletta and Chiappetta (1994) recognize that student's interest and motivations help to perform the educational tasks more pertinently and efficiently. Dzama and Osborne (1999) study the causes of poor performance among African students, including the interaction between traditional cultures and science. They find that poor performance in science among African students is caused by the absence of vocational incentives rather than by the conflict between science and African traditional values and beliefs. They argue that conflict between science and traditional beliefs and values is not peculiar to Africans.
Students' motivation is crucial for better academic results when it is complemented with basic resources or assets. The access to inputs such as books, computers, internet, and educative software could provide alternative ways to see knowledge and it also may help the students to foster their skills.4
Most of this literature has been concerned with the analysis of this relation, but the empirical strategies are essentially correlations. In contrast to these studies, we try to provide new evidence by recognizing the difficulties in the estimation of the effect of motivations on achievement. At the same time, our strategy allows us to estimate whether the effect is similar along the distribution. The interpretation of the contribution of motivation is subject to country-fixed effects and the fact that any measure of motivation is always subjective.
II. Empirical strategy
We start from the assumption that academic achievement can be understood as an outcome in an educational process in which many factors interact. In particular, the academic achievement (Y) of a student j in the country i can be expressed as:
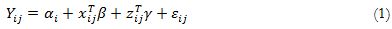
In equation (1), αi captures country-specific effects, z is a vector that includes our variable of interest (index of preferences toward sciences), and x is a vector of control variables. For our purpose, Yij is the score obtained by the student j in the country i at PISA 2006. The term εij is the error. There are three considerations that emerge from the estimation of the parameters in this expression. First, the effect of any particular input on academic achievement could vary over the scores distribution due to its relationship with other factors. Consequently, Quantile Regression is required to obtain more accurate estimations. Second, given the unobserved differences between countries it is also necessary to take into account the fixed effects associated to each country. Third, it is possible that there is endogeneity in the relationship between motivation and achievement: Better performance increases motivation and higher motivation improves performance. We first explain the strategy adopted for the estimation of the coefficients along the distribution and, secondly, we tackle the endogeneity problem.
Koenker (2004) points out that the introduction of fixed effect can inflate the variability of estimates, so a penalty factor must be included on the likelihood function. Assuming that each unit i (country) has mi observations (students), the new minimization problem of Quantile Regression including fixed effects is given by:
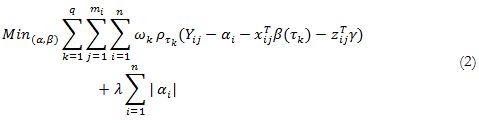
The first summand of equation (2) denotes the classical problem of Quantile Regression as Koenker and Bassett (1978) proposed; ρτk is the linear quantile loss function, and ωk controls the relative influence of the kth quantile on fixed effect parameters. The last term included by Koenker (2004) is the penalty factor. So, if, 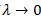 , fixed effects can be estimated; but when
, fixed effects can be estimated; but when 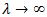 it must be that
it must be that 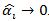 .
.
Since our variable of interest, motivation, is difficult to measure, the empirical strategy adopted to proxy for self-motivation implies the construction of an index based on the available information in the database.5 Many case studies use other measures of motivation such as awards or public mentions; but, in our view, these experiments are more prone to measure external rather than internal motivations. Using the information on preferences towards sciences self-reported by pupils in the PISA student questionnaire, it is possible to have a measure of the pupils' interests. The question: 'how much interest do you have in learning about the following topics (Physics, Chemistry, Biology of Plants, Human Biology, Astronomy, Geology, and experiments' design)?' has the following possible answers: high interest, medium interest, low interest and no interest.
This question may be read as an index of internal or intrinsic motivation, since it does not include elements like external rewards and the answers are not known by teachers or parents. As it can be seen, this is one of the possible approximations to motivation. The implications of this approach have to be read carefully and they belong to the characteristics of the variables and the method used for its construction. Then, we opt for not generalizing the implications obtained from our methodology.
The set of answers are used to construct two different composite indexes. First, we use principal components to get a score from their motivation toward these science topics. Second, we construct an index based on the linear aggregation of the answer in a non-weighted variable. Although the range of the index varies in each case, the ordering of the individuals with respect to these indexes is the same. Since both specifications provide us with very similar findings, we stick to the latter.
As it is common in the literature, the presence of potential endogeneity requires the use of any instrument for reducing the potential bias. The instrument we use is constructed by using the answers on how much does the student agree with a specific set of statements about the role of science in her life.6 The perceived importance of scientific issues is an important source of motivation; however, it does not necessarily imply higher grades in assessments (i.e., the instrument is excludable). In other words, the importance that students attach to scientific topics would affect their performance on the academic assessments only indirectly through its effect on self-motivation. It is easy to accept that motivation on a specific topic increases the effort towards studying it, and both motivation and effort have a positive effect on students' performance. Similarly, good academic results may increase the motivation for deepening in knowledge about this topic. This index could diminish the endogeneity problem. If a student considers that science is important for her life and for society, she has motives to learn more about it but it does not necessarily improve her scores.7
Suppose that the Educational Production Function could be represented by the following expression:

where the educational achievement of the student i (Yi) is only a function of a known vector of inputs X (physical inputs). In that case, the estimated coefficient for the effect of each xi assumes that cov(xi, vi) = 0. However, if an additional unobservable variable Z such as motivation also affects students' learning, the estimated effects of the X inputs will be biased upwards. That is, we overestimate the effect of other inputs due to the positive relationship between motivation and academic achievement. Now, by including an additional variable representing the role of motivation, we have the following expression:

This includes an additional variable into the set of explanatory variables. At this point, the interpretation of the estimated coefficients should recognize: i) measurement problems resulting from omitted variables, and ii) measurement problems in the proxies used for controlling unobserved factors. As we do not have information about the true motivation, the estimations should be interpreted with caution. Our available proxy (the students perception index) q allows us to have an idea about it if E(y|x,z,q) = E(y|x,z). This condition implies that q is redundant when we have controlled for z and it also allows us to fulfill the exclusion restriction. Then, by including any proxy satisfying this condition, we could reduce measurement problems resulting from omitted variables. Under the assumption that our instrument q is not correlated with the error-term, we should have δ = cov(q,Yi)/cov(q,Z). Since we cannot check whether cov(q, vi) = 0, the identification of the coefficient δ depends on the quality of the instrument employed. This is crucial for the size of the effect and the implications on the educational outcomes. In our particular case, we think there is no reason to doubt about the positive relation between the motivation index and the students' perception index (i.e. the relevance of the instrument). Nevertheless, the instrument might be picking up the effect of a non-observable, and this threatens its exogeneity. In particular, one can think that more capable students are also the ones attaching a higher importance to scientific issues; and due to their ability, they are also the ones that perform best during the test. With this in mind, we include a battery of control variables that should capture the confounding effect of non-observables (e.g., ability), allowing us to minimize the risk of having an endogenous instrument. In this regard, variables such as the socioeconomic status, including the parents' educational level, can serve as a proxy for the pupils' skills (see, for instance, Sacerdote, 2002). The point is whether the existence of unobserved factors over-estimates the effect of motivation or not. In what follows, we do our best to reduce this problem.
One emerging issue is that our variable of interest might be affected by the instrument through an additional channel.8 As a consequence, the effect of the variable Z on the outcome (Yi) includes two terms once we instrumented for q. The second term β2α1 reflects the effect of the instrument Z on Y by means of the instrumented variable. We assume that this component is positive. Instead, the term β1γ1 is the alternative channel. In this case, the effect of the instrument (student perception index) on other covariates such as x2 should determine the sign of the bias. For example, it is possible that increases in motivation also have an effect on academic outcomes through the way of using academic assets. Under this assumption, if there is any effect of students' perception about the importance of sciences for human life on any other factor, this should be a positive effect (β1γ1 > 1). In that case, our estimation might be a lower bound on the effect of motivation.
Given that our main interest is to analyze whether there exists different effects along the distribution, the instrumental exercises used in the paper are based on Chernozhukov, Hansen and Jansson 2007; Chernozhukov and Hansen 2008; and Powell 2009. In particular, this approach starts from the Koenker and Bassett (1978) approach, but recognizes the possible endogeneity into the relation. In their work, Chernozhukov and Hansen (2008) estimate the coefficients at each τ - quantile, construct the moments to estimate the conditional quantile function of our outcome (Yi), given the instrument and the set of exogenous covariates. Their strategy increases the efficiency of the robust inference analysis due to the inclusion of the endogeneity problem into the estimation of each quantile's effect.9
III. Data
PISA is an international initiative managed and oriented by the OECD to compare academic achievement between their members. Nowadays, this test is also used in other non-OECD countries around the world.10 It is carried out every three years since 2000 with a special emphasis each time (Reading in 2000, Mathematics in 2003, Science in 2006, Reading in 2009, and again Mathematics in 2012). In contrast to other academic tests, PISA seeks to assess not merely whether students can reproduce what they have learned, but also to examine how well they can extrapolate it to understand novel settings. PISA 2006 is focused on the following aspects: Knowledge of scientific concepts, contexts in which students encounter scientific problems and relevant knowledge and skills are applied (e.g., decision making in relation to personal life, understanding world affairs), and the existence of students' attitudes towards science (for details, see OECD 2009). In contrast to other international academic tests, PISA includes some questions in which students are required to construct their own answers as well as multiple-choice questions.
The sample of students in PISA 2006 comes from a two-step random selection process. First, a sample of schools in each country was chosen. Second, in each school a sample of 15-years old students was extracted. As a result of this process, about 330,000 students were randomly selected, representing about 20 million from 57 participating countries. Yet it is important to highlight that the conditions used in the sampling process make our findings valid only for those staying in the educational system, and not having repeated too many grades.
Our dependent variable to measure school performance will be the pupil's score in science at PISA 2006 provided by the OECD database. This score is a plausible value resulting from using the Item Response Theory, which provides an accurate and comparable cognitive measure between countries and over time. PISA scores are also used to classify pupils by scientific proficiency levels.11 For example, pupils classified in higher levels have more developed scientific knowledge, and thus are more capable of applying science to different situations. The low academic performance in Latin American countries is evident when we see the portion of their population belonging to the sixth level (see appendix 3).
It is also evident that OECD countries outperform in sciences the rest of the countries in the sample (See Figure 1.a). Latin American countries have similar performance as the rest of non-OECD countries (there is not statistical difference between them), but with less dispersion, mainly because the latter is a more heterogeneous group of countries (e.g., Hong Kong, Jordan, and Lithuania. See appendix 3). A more intriguing result is obtained from the density functions from a sample of countries (Figure 1.b). The U.S. shows a great standard deviation, even compared with that of commonly labeled as unequal countries such as Brazil and Colombia. The difference between the country with the lowest average performance (Kyrgyzstan) and the one with the highest (Finland) is evident: Both density functions have their modes quite separately, have almost no common area and have almost the same dispersion (see appendix 3 for details about the results for each country).
Regarding our hypothesis on the positive impact of self-motivation on a student's performance, we compute the density functions by a self-motivation level (quartiles) and found that the change in the density function is slight but significant (Figure 2).12
The sample used in this paper exhibits some well-known characteristics that are common in the literature. Mean and standard deviation of each explanatory variable by scores quartile are summarized in Table 1. It is found an overrepresentation of private schools' students as well as students with higher possessions (academic assets) on the top of the distribution (Table 1). In other variables, differences are not statistically significant among the selected quartiles. That is, average levels of self-motivation seem to be positively related to scores, but this relationship is not significant as a consequence of its variance. As it can be seen, every variable exhibits important variations in both indicators across the selected quartiles. By comparing quartile one against four, educative assets' mean increases from to , while its standard deviation diminishes by a 45%. In the case of self-motivation, both the self-motivation index and the instrument (student's perception index) report significant differences, mainly with respect to quartile four, and direct correlations with pupils' scores are observed.
In order to isolate confounding factors into the analysis of the effect of motivations, some controls are included. Thus, we include control variables that may be classified in three groups: i) individual effects (gender, scientific skills, and mothers' schooling); ii) schools' characteristics (private or public, and gender composition); and iii) location fixed effects (OECD membership, size of the city). Gender, mothers' educational level, type of school (private or public) and location effects are included as dummy variables. That is, female, less than college, private, non-OECD, and village are the reference categories. In this subset, we also include an index of academic assets available at home measured as the sum of four dummy variables associated to the possession of a desk to study, a computer, educational software, and internet access.13 As mentioned above, these controls should minimize the risk of endogeneity caused by a correlation between our instrument and non-observed variables.
The inclusion of academic assets provides additional information about capital stock beyond the traditional approach used in the cross-country literature (number of books, laboratories or teachers). It is assumed that access to ICTs fosters academic achievement for students in modern societies where technological change is constantly increasing and provides alternative channels of knowledge spillovers. Having access to personal computers, internet, and academic software could influence students' performance through at least two other mechanisms. On one side, having access to them facilitates homework, interactions (teacher-student and student-student) and the increase in the productivity of other resources used during the educational process. On the other side, having access or not could have an effect on their motivation with respect to the others. That is, for a given student it is demotivating when her peers have more access to these resources.14
In the case of academic assets, the difference between density functions is more evident.15 Academic assets and students' scores are positively related as expected, but for the self-motivation proxy a nonlinear relationship is observed (Figure 2b). For the three first quartiles, self-motivation seems to affect positively students' performance, but this effect disappears for the last quartile. This result suggests that the effect of self-motivation changes over scores distribution.
We also include a proxy variable for gender interaction within the school, which is measured by the proportion of boys in the school. The purpose of this variable is to obtain information about the importance of coeducation or single-sex schools in terms of class behavior. The rest of the controls are those that are usually included in educational production functions.
IV. Results
The analysis of the effect of motivation on academic achievement is carried out in various steps. In each, we try to solve possible limitations from the data and the statistical processes. First, we start from the estimation of the linear model in equation (1) using Ordinary Least Squares (OLS), (Table 2, col.1). The coefficients are statistically significant (individually and jointly). Our results support that academic assets are positively related with science scores by indicating that academic assets complement students' skills and other educational inputs. The results indicate that being a boy, having a good understanding of scientific issues and having a mother with a high educational level imply higher scores in science on average. Regarding the school characteristics, private schools' students outperform those from public schools; and the score increases with the proportion of boys in the school, in line with the previous literature. All the individual effects considered have the expected sign.
An important unobserved factor is the importance of the educational system in each country. Some societies could be more committed to education than others, which could bias the results. Hence, the implementation of country fixed effects allows us to control for institutional factors characteristic of each country and achieve more accurate estimations. To do so, we use two different approaches. First, we use a Least Squares Dummy Variables estimator -LSDV- by adding one dummy for each country. Second, we subtract the average per country in our outcome variable 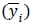 from equation (1) and get the usual fixed effects expression:
from equation (1) and get the usual fixed effects expression:
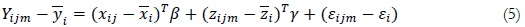
The estimated coefficients are shown in Table 2, column 2 and 3, respectively. This strategy has an impact on school fixed effects as a consequence of the sample size. The estimated coefficients suggest that the explanatory variables' marginal effect decreases when a control for country effects is included. In all cases, the estimated models are jointly significant. When unobservable heterogeneity is controlled for, self-motivation and students' scores are positively related.16 By assuming that it represents the country-level fixed effects, the estimations summarized in column (3) are more efficient than those of column (2) because it allows us to compute the fixed effects but also the loss of degrees of freedom is lower. The rest of the variables exhibit the expected significance and allow us to control for other factors.
Nevertheless, it might as well be the case that the endogeneity problem persists even after controlling for country effects. In order to account for this, we estimate an instrumental variables model including student perception index as instrument (column 4). Our coefficient of interest is still positive and significant, but is higher than in the previous specifications. The first stage shows that there is a positive correlation between the student perception index (instrument) and the self-motivation index (see Appendix 2).17 This finding is not free of criticism. Our estimations suggest that we have a lower bound of the real effect after recognizing other alternative channels.
The size of the effect of changes in motivation on academic performance is subject to the country fixed effects. However, if it is assumed that these fixed effects are equal among countries, an increase in one standard deviation in the motivation index will increase academic outcomes in 1/6th of its standard deviation. As Sula (2008) states, a constraint emerges as a consequence of the fact that interpretation of country-level effects in Quantile Regression models is unclear (Sula 2008).
In order to assess the effect of our independent variables on different points of the sciences score conditional distribution, we estimate our coefficient of interest by Instrumental Variables Quantile Regression models. This step goes beyond Koenker and Bassett (1978) approach because it also includes country effects (Powell 2009) and instrumental variables (Chernozhukov et al. 2007; Chernozhukov and Hansen 2008). The IV estimation along the distribution using the students' perception index is carried out through a two-stage procedure (Table 3). The estimation results are robust, i.e. they do not present important changes and the coefficients linked to self-motivation report the appropriate sign. Regarding our hypothesis, self-motivation has a positive effect but decreases along the distribution. Since we do not have a sample where some of them have been treated and others act as a control, the quality of the results should be read carefully. In our view, the importance of motivation in academic achievement is probably higher due to the fact that one pupil can be affected through different channels, but the controls added to the estimation allows us to see whether the effect is stable to the set of controls.
This is an interesting result because it provides evidence that student populations with very different characteristics and educational outcomes enjoy distinct added values from motivation. Then, providing public initiatives in sciences such as staging 'attractive' experiments, organizing scientific fairs and other interventions oriented to increase the perceived utility from learning could increase educational outcomes when they are focalized on specific groups.18 If it is assumed that motivation increases academic performance among students, the change in the estimated coefficients suggest that their importance is relative to the rest of the inputs and, consequently, public policies should use focalized strategies in order to increase overall motivation.
The importance of our main variable of interest on academic achievement decreases with quantile, but it is always positive. This indicates that for students with the poorest performance, the effect of programs or policies designed to improve their motivation could have a relatively higher impact on their academic achievements.
Given the expected positive relationship between information access and individual interest on a specific topic, social programs devoted to improve the ICTs coverage would have a positive impact on a student's school performance mean and gap through two channels: i) students with more academic tools perform better (direct channel), and ii) easier access to information has an inertial effect: When a student meets a topic for the first time, and she has easy access to more information on the subject, she would be more motivated to deepen her knowledge on the area (indirect channel).
V. Concluding remarks
Studying the channels through which motivation fosters educational outcomes is an ongoing quest in the educational economics literature. Our findings confirm the intuition that self-motivation is a decisive determinant of academic outcomes. In particular, we show that higher self-motivation is associated to higher scores in a science standardized test. Moreover, there exists a significant difference in the marginal effect of motivation on achievement between the most and less advantaged students. This finding supports the design of focalized policy interventions based on students' performance.
As mentioned above, intrinsic motivations may play a major role when it comes to learning science. Acquiring knowledge in this area is highly associated to some specific components of internal motivations such as a strong inclination to solve more demanding problems and the need to remain focused on particular issues or phenomena. That is, the specific requirements of science literacy imply that students tend to be more successful at improving their knowledge in this area when their intrinsic motivation is higher (see Ryan and Deci, 2000; Gottfried, 1985).
The design of programs oriented to increase the internal utility of studying is an alternative to fill the gap left by inadequately committed parents and teachers. Programs oriented towards children with lower performance and those who do not have access to additional support might have interesting results. Some alternatives as Insights in the US, La main à la pâte in France or Ondas in Colombia are changing the ways of sharing knowledge by using active practices such as applying concepts to everyday life and stimulating participation in scientific events.
After recognizing the fact that one of the factors influencing academic performance is the environment around the pupil, it is necessary to dig deeper into the discussion about the role of 'peer effects' in motivation at the classroom level. Though this aspect goes beyond the main purpose of our study, we devote the next few lines to frame it in the context of the interaction between external an internal motivations. Hoxby (2000) notes that the existence of peer effects is crucial for educational policies in terms of the ability of managing aspects such as sorting in the classroom and gender composition. Teachers should continuously work on students' motivations. But their effort should be both at the individual and the group level. The students' initial degree of motivation could change as a consequence of multiple factors (teachers' behavior, the nature of the assignments, the student-student and teacher-student interactions, the structure of the program, and the didactic materials). Positive external factors can increase teachers' efficiency in terms of total motivation. Negative factors could result in undesired outcomes. For instance, the use of threats as a mechanism to increase motivation can actually back fire: Increasing the use of prizes can decrease students' achievement by creating dependence on them. The evidence suggests that threats such as level repetition have no causal effect on academic achievement (Vandenberghe and Belot, 2010). Furthermore, the use of external rewards may also generate adverse effects as envy, and this could explain why some outstanding pupils are so unpopular and targeted for harassment or bullying (see, Bishop 2006).
The identification of individual (self-motivation) and external factors (peer effects and external rewards) on academic performance is still a task for future research. So far the literature has recognized that the measurement of peer effects is not free of bias, and more importantly for this case is the impossibility of isolating family, school and neighbor effects. The use of a quantile regression with instrumental variables allows us to reduce possible bias and to provide a lower bound on the effect of motivation on academic performance. However, it is necessary to say that this is an ongoing task that requires more elements to provide unbiased estimations.
The most important conclusion from this paper is the relevance of one of the intrinsic motivation's dimension on academic performance (self-motivation). Specifically, the existence of different coefficients over the entire distribution calls attention over the fact that it is necessary to continue working on the impact of intrinsic and extrinsic motivations on educational achievement using distinct strategies designed to populations with different socioeconomic backgrounds.
From the policy perspective, governments in less developed countries should aim at increasing their investments in the use of modern didactic tools. This strategy should have a positive impact on motivational levels and reduce the cost of acquiring information. Moreover, it should help to compensate for the absence of other inputs (e.g., low parental involvement, or low economic and academic assets). The discussion on how to increase internal motivation and seek alternative proxies for testing it is still a challenge.
Notes
2 Extrinsic motivation appears when the degree of a student's effort depends on external rewards (public approval, awards or some kind of object). See Deci, Vellerand & Ryan (1991) and Deci, Koestner & Ryan (1999) for a detailed discussion.
3 Woessmann (2003) says that grading relative to class performance gives students an incentive to lower average class performance because this allows the students to receive the same grades at less effort. The cooperative solution of students to maximize their joint welfare is for everybody not to study very hard. Students also have incentives to distract teachers from teaching a high standard and to apply peer pressure on their classmates for not being too studious with grades relative to the class level (Bishop 1999).
4 See Oliver and Simpson 1988 and Nasr and Soltani, 2011 for other studies on the role of motivation in learning.
5 In this paper, we assume that internal motivation is equivalent to intrinsic motivation or self-motivation.
6 The index uses the answers (Strongly agree, Agree, Disagree, Strongly disagree) to the following question: How much do you agree with the statements below?: a. Advances in broad science and technology usually improve people's living conditions; b. Broad science is important for helping us to understand the natural world; c. Some concepts in broad science help me see how I relate to other people; d. Advances in broad science and technology usually help improve the economy; e. I will use science in many ways when I am an adult; f. Science is valuable to society; g. Science is very relevant to me; h. I find that science helps me to understand the things around me; i. Advances in science and technology usually bring social benefits; j. When I leave school there will be many opportunities for me to use science.
7 The choice of this instrument is based on its simple correlation with the self-motivation index. For the case of PISA, this figure is higher than 0.6.
8 Suppose that we have the expression (Zi = α0 + α1qi + ui) that shows the relation between the instrument (q) and our variable of interest. It can be assumed that α1 > 0 and the expression X2 = γ0 + γ1qi + ei exhibits an additional channel through which the instrument could have an effect on academic achievement. Then, by solving it, we obtain that Yi = θ0 + (β1γ1 + β2α1)qi + εi
9 Formally, the process consists of solving the following problem: argminα(τ) E ρτ[y - d'α(τ) + xβ(τ) - z'γτ, being τ-quantile, X the controls and Z is the instrument. For details, see Chernozhukov and Hansen (2008).
10 PISA 2006 database includes information about several aspects from the environment of the student (personal characteristics and family backgrounds), schools' characteristics (schools' resource endowments and location), and students' habits and hobbies, among other aspects.
11 According to scores, band definition of each level is: level one (bellow 409.5), level two (409.5 to 484.1), level three (484.1 to 558.7), level four (558.7 to 633.3), level five (633.3 to 707.9), and level six (above 707.9).
12 The Kruskal-Wallis test (K-W) rejects the equality between the scores distributions by self-motivation level.
13 Each asset has the same value in the index, thus the index goes from 0 to 4. Nonetheless, there is a positive correlation between the possessions of each asset which allows us to sort the people according to their utilization of information and communication technologies.
14 The technological component immerse in learning materials is notorious and reveals the involvement of parents in their children's educational process. In some cases, it seems that access to computer at school does not have a considerable effect (Barrera-Osorio and Linden (2009) Linden (2008)), but in this document we deal with access at home.
15 Density functions are different not only in position but also in shape. This observation is also validated through the Krustall-Wallis (K-W) test.
16 Using an F-test, significant differences among fixed effects were found.
17 This estimation was also performed for two sample partitions: OECD and non-OECD countries, and the results remain. The size of the estimated coefficients goes in the same direction of economic development and sample size. They are available upon request.
18 The marginal effect of city size decreases and the skills index has a non-monotonic shape. Mothers' schooling does not differ from the OLS estimation.
References
American Association for the Advancement of Science (1989). Science for All Americans. Oxford: Oxford University Press.
Al-Samarrai, Samer (2002). ''Achieving education for all: How much does money matter?'', Journal of International Development ,Vol. 18, Issue 2, pp. 179-206.
Barrera-Osorio, Felipe, and Linden, Leigh (2009). ''The use and misuse of computers in education evidence from a randomized experiment in Colombia'', Impact Evaluation Series, No. 29, WPS4836, pp. 1-41.
Betts, Julian (1996). ''The role of homework in improving school quality'', Discussion Paper 96-16, pp. 1-45.
Bishop, John (1989). ''Is the test score decline responsible for the productivity growth decline?'', American Economic Review, Vol. 79, Issue 1, pp. 178-197.
Bishop, John (1992). ''The impact of academic competencies on wages, unemployment, and job performance'', Series on Public Policy Vol. 37, pp. 127-194.
Bishop, John (1997). ''The effect of national standards and curriculum-based exam on achievement'', American Economic Review. Papers and Proceedings, Vol. 87 (2), pp. 260-264.
Bishop, John (1999). ''Are national exit examinations important for educational efficiency?'', Swedish Economic Policy Review, Vol. 6, pp. 349-398.
Bishop, John (2006). ''Drinking from the fountain of knowledge: Student incentive to study and learn. Externalities, information problems, and peer pressure''. In: Eric A. Hanushek and Finis Welch(Eds.), Handbook of the Economics of Education (pp. 909-944) Amsterdam, North Holland.
Bishop, John; Bishop, Matthew; Gelbwasser, Lara; Green, Shanna and Zuckerman, Andrew (2003). ''Nerds and freaks: A theory of student culture and norms'', Brookings Papers on Education Policy, No. 6, pp. 141-213.
Boissiere, Maurice; Knight, John and Sabot, Richard. (1985). ''Earnings, schooling, ability, and cognitive skills'', American Economic Review, Vol. 75, Issue 5, pp. 1016-1030.
Chernozhukov, Victor, and Hansen, Christian (2008). ''Instrumental variable quantile regression'', Journal of Econometrics, 142, Issue 1, pp. 379-398.
Chernozhukov, Victor, Hansen, Christian and Jansson, Michael (2007). ''Inference approaches for instrumental variable quantile regression'', Economics Letters, Vol, 95, Issue 2, pp. 272-277.
Coleman, James; Campbell, Ernest; Hobson, Carol; Mcpartlet, James; Mood, Alexander., Weinfeld, Frederic & York, Robert. (1966). Equality of educational opportunity, Washington, D.C., Government Printing Office.
Colletta, Alfred & Chiappetta Eugen (1994). Science Instruction in the Middle and Secondary School, New York, Macmillan Publishing.
Cooper, Harris (1989). Homework, White Plains, Longman.
Deci, Edward; Koestner, Richard & Ryan, Richard (1999). ''A meta-analytic review of experiments examining the effects of extrinsic rewards on intrinsic motivation'', Psychological Bulletin, Vol. 125, Issue 6, pp. 627-668.
Dzama, Emmanuel & Osborne, Jonathan (1999). ''Poor performance in science among african students: An alternative explanation to the african worldview thesis'', Journal of Research in Science Teaching, Vol. 36, Issue 3, pp. 387-405.
Eisenberger, Robert; Pierce, David & Cameron, Judy (1999). ''Effect of external reward on intrinsic motivation- negative, neutral and positive'', Psychological Bulletin, Vol. 125, Issue 6, pp. 677-691.
Eisenkopf, Gerald (2008). ''Peer Effects, Motivation, and Learning University of Konstanz'', Department of Economics, Unpublished manuscript.
Fuchs, Thomas & Woessmann, Ludger (2008). ''What accounts for international differences in student performance?: A re-examination using PISA data'', Empirical Economics, Vol. 32, Issue 2-3, pp. 433-464.
Gottfried, Adele. (1985) ''Academic Intrinsic Motivation in young elementary and junior high students. Journal of Educational Psychology'', Vol. 77, Issue 6, pp. 631 – 645.
Hanushek, Eric (1998). ''Conclussion and controversies about the effectiveness of school resources'', Economic Policy Review, Vol. 4, No. 1, pp.11-28.
Hoxby, Caroline (2000). "Peer Effects in the Classroom: Learning from Gender and Race Variation," NBER Working Papers, No. 7867, p.1-64.
Koaler, Olaf; Baumert, Jünger and Shnabel, Kai (2001). ''Does interest matter? The relationship between academic interest and achievement in mathematics'', Journal for Research in Mathematical Behavior, Vol. 32, Issue 5, pp. 448-470.
Koenker, Roger (2004). ''Quantile regression for longitudinal data'', Journal of Multivariate Analysis , 91, pp. 74-89.
Koenker, Roger, & Bassett, Gilbert (1978). Regression quantiles. Econometrica, Vol. 46, No.1, pp. 33-50.
Lazear, Edward (2001). ''Educational production'', ''Quarterly Journal of Economics'', Vol. 116, No. 3, pp. 777-802.
Lee, Jong-Wha & Barro, Robert (2001). ''Schooling quality in a cross section of countries'', Economica, Vol. 68, No. 272, pp. 465-488.
Linden, Leigh (2008). ''Complement or substitute? The effect of technology on student achievement in India'', Columbia University, Mimeo.
Nasr, Ahmad & Soltani, Asghar (2011). ''Attitude towards biology and its effect on students achievement'', International Journal of Biology, Vol 3, No. 4, pp. 100-104.
OECD (2009). ''Pisa 2006: Technical Report''. Organisation for Economic Co-operation and Development, available at: www.pisa.oecd.org (Octubre 10 de 2012).
Oliver, J. Steve & Simpson, Ronald (1988). ''Influences of attitude towards science, achievement motivation, and science self concept on achievement in science: A longitudinal study'', Science Education, Vol. 72, Issue 2, pp. 143-155.
Powell, David (2009). ''Unconditional quantile regression for panel data with exogenous or endogenous regressors''. RAND Labor and Population Working Paper,WR-710, pp. 1-39.
Sacerdote, Bruce (2002). ''The nature and nurture of economic outcomes'', American Economic Review, Vol. 92, No. 2, pp. 344-348.
Sharma, Dhiraj (2010). ''Incentives for academic achievement: An experimental study''. In: 2010 Annual Meeting of the Agricultural and Applied Economics Association, July 25-27, Denver, Colorado.
Sula, Ozan (2008). ''Demand for international reserves: A quantile regression approach'', MPRA Paper, No 11680, pp. 1-20.
Vandenberghe, Vincent & Belot, Michèle (2010). ''Evaluating the "threat" effects of grade repetition. Exploiting the 2001 reform by the French-speaking Community of Belgium''. In: Mancebón, María Jesús; Pérez, Domingo; Gómez, José María and Giménez, Gregorio (Eds.), Investigaciones de Economía de la Educación (vol 5.) (pp. 185-204). España, Asosiación de Economía de la Educación. Available at: http://repec.economicsofeducation.com/2010zaragoza/05-09.pdf
Walter, Janet & Hart, Janelle (2009). ''Understanding the complexities of student motivations in mathematics learning'', Journal of Mathematical Behavior, Vol. 28, Issue 1-2, pp. 162-170.
Woessmann, Ludger (2003). ''Schooling resources, educational institutions, and student performance: The international evidence'', Oxford Bulletin of Economics and Statistics, Vol. 65, Issue 2, pp. 117-170.
Appendix