
ARTÍCULOS
Prueba de sesgo sobre rendimientos financieros en el mercado colombiano
A skew test on financial returns in the Colombian market
Un test de biais pour analyser les rendements financiers du marché colombien
Marisol Valencia*; Alejandro Bedoya**
* Investigadora y PhD(c) Universidad Nacional de Colombia. Dirección postal: Carrera 75 # 32-52, Medellín, Antioquia, Colombia. Dirección electrónica: mvalencia@unal.edu.co
** Investigador y docente Universidad Nacional de Colombia. Dirección postal: Calle 77DD # 85B – 47, Medellín, Antioquia, Colombia. Dirección electrónica: jabedoyav@unal.edu.co
–Introducción. –I. Índice General De La Bolsa De Valores De Colombia (IGBC). –II. Distribución Normal y T Sesgada. –III. Métodos. –IV. Resultados. –V. Discusión de resultados. –Conclusiones. –Referencias.
Primera versión recibida el 8 de agosto de 2013; versión final aceptada el 15 de noviembre de 2013
RESUMEN
La caracterización de los rendimientos financieros depende, en gran medida, de su comportamiento probabilístico, el cual puede ser mal ajustado, conduciendo así a malas decisiones económicas relacionadas con valoración de activos, asignación de cartera y/o medición del riesgo de mercado. En este trabajo se propone una prueba que permita determinar el ajuste de los rendimientos del Índice General de la Bolsa de Valores de Colombia (IGBC) a las siguientes distribuciones: Normal, Normal Sesgada y T Sesgada. Además, se mide el nivel de sesgo y se compara el desempeño de la prueba propuesta con otra prueba existente, usada únicamente para la detección de asimetría. Se encuentra que la prueba propuesta permite caracterizar los rendimientos del mercado de valores colombiano con una de las distribuciones de probabilidad, a diferencia de la otra prueba, que sólo advierte sobre la existencia de sesgo y no establece la distribución que representa su comportamiento.
Palabras clave: Decisiones de Inversión, Economía Financiera, Distribuciones Específicas, Comportamiento Financiero.
Clasificación JEL: G11, P34, C46, G02.
ABSTRACT
The characterization of financial returns depends heavily on probabilistic behavior, which can be ill-fitted, thus leading to inappropriate economic decisions concerning asset pricing, portfolio allocation and/or the measurement of market risk. In this paper, we propose a test to determine the adjustment of the returns of the General Index of the Colombian Stock Exchange (IGBC) to the following distributions: Normal, Skew Normal, and Skew T. In addition, we measure the level of bias and compare our test's performance with an alternative test used only for detecting asymmetry. We find that the proposed test allows for characterizing returns in the Colombian stock market with one of the probability distributions, unlike the other test, which only provides a warning about the existence of bias and does not ascertain the distribution representing its behavior.
Key words: Investment Decisions, Financial Economics, Specific Distributions, Behavioral Finance.
JEL Classification: G11, P34, C46, G02.
RÉSUMÉ
La caractérisation des rendements financiers dépend en grande partie de leur comportement probabiliste. Celui-ci peut être mal calculé, ce qui conduit à des mauvaises décisions économiques dans l'évaluation des actifs, dans le choix de portefeuilles ou bien dans la mesure du risque de marché. Cet article propose un test qui permet de déterminer l'ajustement des rendements de l'Indice Général de la Bourse de Colombie (IGBC) sur les distributions suivantes: normale, normale biaisée et T biaisé. Le niveau du biais est mesuré pour ensuite établir une comparaison avec la performance du test avec un autre test existant, lequel n'est utilisé que pour la détection de l'asymétrie. On constate que, effectivement, le test proposé caractérise les rendements du marché boursier colombien, à différence d'autre test qui ne font qu'avertir l'existence d'un biais sans déterminer la distribution qui explique le comportement des rendements.
Mots-clés: décisions d'investissement, économie financière, distributions spécifiques, comportement financier.
Classification JEL: G11, P34, C46, G02.
Introducción
Los índices bursátiles, como el Índice General de la Bolsa de Valores de Colombia (IGBC), permiten describir la percepción del mercado frente al comportamiento de las empresas y la economía, y muestran una medida de desempeño del sector económico real. Su análisis y su caracterización permiten gestionar los portafolios y realizar gestión de riesgos de mercado (Caicedo, Claramunt & Casanovas, 2011a y 2011b; Grajales y Pérez, 2010; Dubova, 2005).
Dichos índices son monitoreados, evaluados y modelados, con el fin de realizar predicciones acerca de su movimiento, estimación de la oferta y demanda de activos financieros y la cuantificación del riesgo. Lo anterior se considera insumo principal en la toma de decisiones. Es por esto que una adecuada caracterización de los rendimientos del IGBC, precisa un mayor acierto en la decisión de inversión.
Con relación a la posible existencia de sesgo y dependencia en los rendimientos, Mandelbrot & Hudson (2006), y Peters (1994), señalan que una de las principales características de estos es el no cumplimiento de la normalidad y la larga dependencia. Esto es validado en el mercado local por los autores Pérez & Fernández (2006), quienes además revisan el modelo de heteroscedasticidad condicional autorregresiva (ARCH) para modelar el comportamiento del IGBC. Fernández (2010a; 2010b) realiza un ajuste del modelo exponencial GARCH sobre el IGBC, el cual permite incorporar mejor la variación de la volatilidad inherente a este. Chunhachinda et al.(1997) determinan la asimetría en rendimientos bursátiles usando un método de optimización, sin embargo, no determinan bondad de ajuste a una distribución específica. Ninguno de los anteriores autores han propuesto la detección de sesgo dinámico como lo hacen Duran, Lorenzo, & Ruiz (2013), quienes diseñan un modelo GARCH agregando dicha variación dinámica en el sesgo, realizando una transformación sesgada sobre los rendimientos; sin embargo, no buscan un ajuste distribucional general, sino una modelación. Por el contrario, en este trabajo se resalta la importancia de caracterizar la serie de tiempo de rendimientos usando dos distribuciones diferentes a la Normal, de forma descriptiva: la Normal y la T Sesgada. Estas introducen un parámetro de sesgo λ a las originales Normal y T de Student (Azzalini & Dalla Valle, 1996; Azzalini & Capitanio, 1999; Arellano, Bolfarine & Lachos, 2005; Bolfarine, Montenegro & Lachos, 2007).
Con el fin de identificar comportamientos sesgados sobre cualquier variable aleatoria, se han propuesto diferentes pruebas, entre ellas: Lisi (2007), que propone la detección de asimetría usando bootstrap, o Valencia (2010), que propone una prueba para detectar el ajuste a las distribuciones Normal o T Sesgada para los residuales de los modelos lineales mixtos.
En el presente trabajo se pretende compararla aplicación de la prueba de Lisi (2007) para detectar asimetría en los rendimientos financieros, con respecto a Valencia (2010) que permite detectar ajuste a las distribuciones Normal, Normal Sesgada y T Sesgada. La segunda prueba será validada vía simulación, mostrando la proporción de aciertos bajo un número de simulaciones de variables aleatorias bajo las tres distribuciones respectivas. Con esto, tanto la primera como la segunda prueba darán un criterio de existencia de sesgo en la distribución de dichos rendimientos; sin embargo, la segunda prueba proporcionará una bondad de ajuste, midiendo la proporción de puntos por fuera de las bandas teóricas. Adicionalmente, se propone una variación a Valencia (2010) para medir un nivel de sesgo con un algoritmo de optimización, el cual es un valor agregado que permite mejorar el ajuste a la distribución sesgada encontrada.
I. Índice General De La Bolsa De Valores De Colombia (IGBC)
El IGBC es un indicador del mercado accionario de la Bolsa de Valores de Colombia. Este refleja el comportamiento promedio de los precios de las acciones en el mercado ocasionado por la interacción de la oferta y la demanda, producto de las negociaciones de dichas acciones (Banco de la República1), permitiendo que se visualice la variación de los precios en el tiempo.
Acorde con la definición dada por Vera (2005), el modelo matemático se basa en un promedio ponderado de los precios de las acciones más representativas del mercado, de manera que muestra el comportamiento individual de dicho precio.
La relación entre el interés compuesto y el capital (precio) se pone de manifiesto en la ecuación financiera del valor futuro dado un valor presente (F|P), que permite la acumulación de intereses, capitalizándolos en cada uno de los períodos respectivos.
Si se tiene un capital P, expresado en unidades monetarias y se invierte en el momento t=0 a la tasa de interés (rendimiento) efectiva con capitalización continua(r), la cantidad de dinero que se obtendría para el primer periodo, futuro F1, (momento t=1) sería (Hull, 2009):

Es por esta relación que el interés en los estudios financieros se centra en la caracterización de los rendimientos (r) para diferentes períodos de tiempo.
En este trabajo el análisis se enfoca en el ajuste distribucional del comportamiento de los rendimientos, y la medición del parámetro de sesgo y la caracterización del sesgo λ existente.
II. Distribución Normal y T Sesgada
A. Distribución Normal Sesgada
En la función densidad de probabilidad Normal Sesgada, acorde con Azzalini (1985), una variable aleatoria y sigue una distribución Normal Sesgada con parámetros de localización µ, escala o varianza σ2, y sesgo λ, con función densidad de probabilidad dada por:
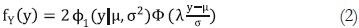
Cuando λ=0, esta se reduce a la distribución Normal común.
B. Distribución T Sesgada
Vernic (2005) señala la distribución multivariada Skew T generalizada, definida así:
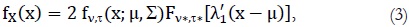
donde Fv,τ(x; u, Σ) es la fdp de la distribución T generalizada multivariada, mientras Fv*,τ*[λ1'(x - u)] es la forma de la distribución univariada generalizada estándar.
III. Métodos
El procedimiento de este trabajo inicia con el análisis descriptivo del comportamiento de las series de los rendimientos para cuatro períodos de tiempo del IGBC, su dependencia, empleando las gráficas de ACF, PACF y la prueba de Box-Pierce. Adicional a esto, se identifica si provienen de un comportamiento con distribución Normal utilizando la prueba de Jarque Bera.
Posterior a esto, se aplica la prueba propuesta por Lisi (2007), para determinarla existencia de asimetría en los rendimientos; y la de Valencia (2010), con la cual se determina el ajuste de distribución más adecuado y se estima el nivel del sesgo que alcanza dicha variable para las distribuciones adecuadas, encontrando, con el algoritmo de optimización, el valor que minimiza la proporción de puntos no incluidos en las bandas de la respectiva distribución.
A. Prueba de Lisi
Lisi (2007) propone una prueba para la detección de la asimetría cuando los datos poseen dicho comportamiento. A continuación se realiza una descripción de la aplicación de la prueba de Lisi.
Suponiendo que el proceso de generación de datos es estacionario, este puede ser descrito por una caminata aleatoria que suma su media ut más un error et. La media utse asume como la evolución condicional de la media, y et es correlacionado pero no necesariamente independiente u homocedástico. Adicionalmente, se supone que ut es lineal y se puede describir por un proceso ARMA. Con base en el planteamiento anterior, probar la simetría marginal de yt s equivalente a probar la simetría marginal de et. Por ello, en este trabajo, se probará la simetría marginal de yt a diferencia de Lisi.
La prueba utiliza los datos observados para obtener una distribución de tal forma que sea simétrica, y luego la usa para calcular los valores críticos. De lo anterior se plantea el siguiente sistema de hipótesis: H0: Sy = 0 vs H1: Sy ≠ 0. Donde Sy es el parámetro de asimetría de la distribución empírica de la serie. El procedimiento para realizar la prueba es el siguiente:
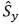 la serie yt.
la serie yt.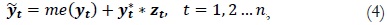
donde y*t se muestrea con reemplazo para la distribución empírica de yt* y zt proviene de una distribución Normal simétrica. La distribución de  representa una versión simétrica de yt. La serie usada para el bootstrap tiene un tamaño de 1000 datos.
representa una versión simétrica de yt. La serie usada para el bootstrap tiene un tamaño de 1000 datos.

B. Prueba de distribución sesgada por bandas
El procedimiento para la prueba parte del siguiente corolario sobre la distribución asintótica del cuantil o fractil ξp, acorde con Valencia (2010).
Corolario: Sea 0 < p < 1. Si F posee una función densidad f en una vecindad de ξp y f es positivo y continuo para ξp, entonces:
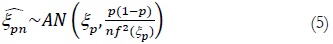
Es decir, su estimación se distribuye asintóticamente Normal con dicha media y varianza.
1. Procedimiento algorítmico de la prueba
El algoritmo fue desarrollado en el software R, utilizando algunas funciones del paquete Sn (diseñado porAzzalini, 1985).
Sea p la proporción acumulada asociada de los cuantiles de la variable de interés: xi = Qp, reales

Se estima:

Donde Q son los cuantiles a graficar de los datos.
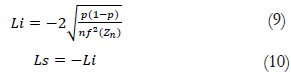
Calcule la proporción de puntos que caen por fuera de las bandas respectivas, para cada distribución.
Realice una prueba de hipótesis estadística de diferencia de proporciones entre los puntos que caen por fuera de las bandas respectivas.
2) Validación vía simulación
Se simula una variable aleatoria bajo las distribuciones Normal, SN o ST; así, la aplicación de la prueba de Valencia (2010) para cada variable debe reflejar el ajuste a la distribución simulada. Este proceso se repitió 1000 veces para cada una, dejando fijos la media y la desviación estándar, y variando el nivel de sesgo λ en cuatro valores: 0.1, 1, 1.5 y 2.
La simulación es descrita en los siguientes pasos:
3) Algoritmo Heurístico Tabú
Con el fin de encontrar el nivel de sesgo que minimice los puntos por fuera de las bandas, y que indique un mejor ajuste posible, se utiliza el algoritmo de búsqueda Tabú, explicada a continuación.
La metodología de búsqueda heurística se fundamenta en la creación de memoria, basada en la lista Tabú, que consiste en la exploración del nivel de sesgo de la distribución teórica respectiva (SN, ST), que se modifica a partir de una combinación de una variable aleatoria uniforme y una Normal, de manera que permite encontrar los valores del sesgo que minimizan la proporción de puntos por fuera de las bandas bajo la distribución buscada. El resultado es un valor muy aproximado al mínimo global, mas no necesariamente este.
Función objetivo:

donde Pfi es la proporción de puntos por fuera de las bandas de la distribución sesgada para el respectivo rendimiento i, con i = 1, 2, 3, 4. (Rendimientos diarios, 5, 10 y 20 días).
Variable de decisión: nivel de sesgo λ.
IV. Resultados
En esta sección se busca aplicar las dos pruebas enunciadas, validar la propuesta y estimar el nivel de sesgo (λ) con el algoritmo de optimización sobre los rendimientos en los precios del índice en el periodo del 29 de junio de 2001 al 11 de abril de 2013. Sobre estos precios se calculan los rendimientos continuos para diferentes subperíodos, a saber: diarios, semanales (5 días), quincenales (10 días) y mensuales (20 días), tomando como referencia que un año bursátil está compuesto aproximadamente por 244 días de negociación, obteniendo series de 2881, 576, 288 y 144 datos, respectivamente.
A. Descripción de datos del IGBC.
El Gráfico 1 muestra el comportamiento histórico para cuatro diferentes series de tiempo. De manera general se puede apreciar la no existencia de tendencia, así como la falta de estacionariedad evidente en la varianza no constante, causada, tal vez, por la existencia de dependencia. Esto será ilustrado con las gráficas ACF, PACF y la prueba de Box-Pierce.
En el Gráfico 2 puede apreciarse una dependencia de corto plazo, aproximadamente de K=1.
La hipótesis nula asociada a esta prueba de Box-Pierce indica que los valores de autocorrelación hasta el k-ésimo rezago son iguales a cero. La Tabla 1 muestra los valores p obtenidos en la prueba contrastados para un nivel de significancia del 5%. Esto permite concluir que para la serie de rendimientos diarios existe dependencia en los rezagos 3, 10 y 20; en los rendimientos de 5 y 10 días hay evidencia de autocorrelación a corto plazo (k=3); para los rendimientos a 20 días no existe evidencia suficiente para afirmar la dependencia ni a corto, ni a largo plazo.
1) Evidencias de no normalidad en las series de rendimientos
El Gráfico 3 ilustra las diferentes densidades en las series de tiempo asociadas a los rendimientos del IGBC, observando una presencia de sesgo en las gráficas. Adicionalmente, en estas se sobrepone la densidad Normal (línea punteada), y se observa el valor P de la prueba de Normalidad Jarque Bera, indicando en todos los casos un valor menor del 5%, lo cual indica la presencia de no normalidad en las serie, como lo confirman las diferencias entre la línea punteada que representa la densidad Normal y la línea continua correspondiente al respectivo rendimiento.
B. Aplicación de prueba de Lisi
La Tabla 2 resume los resultados sobre 100 simulaciones de la aplicación para las diferentes series de tiempo. Vale resaltar que la hipótesis nula en esta prueba afirma que la distribución es simétrica (Sy = 0).
Acorde con los resultados de las simulaciones, los rendimientos de 1, 5, 10 y 20 días sí presentan sesgos o asimetría por su alto porcentaje de rechazo.
C. Prueba de distribución sesgada por bandas
1) Validación via simulación
La validación propuesta fue simulada en el software R y los resultados se observan en la Tabla 3.
La Tabla 3 muestra el número de aciertos acordes con el criterio del ítem 3 del procedimiento algorítmico, implicando un alto nivel de aceptación y por tanto, de validez de la prueba propuesta.
El 50% observado para λ = 2 indica que la simulación de la Normal Sesgada tiene desvíos significativos a medida que se incrementa el nivel de sesgo, reflejando que la variable aleatoria se ajusta más a una T Sesgada que soporta una mayor asimetría en sus colas pesadas.
2) Prueba de bondad de ajuste para rendimientos
Se presentará la prueba de bondad de ajuste de los rendimientos del IGBC, comparando su comportamiento por pares con relación a las distribuciones: Normal, Normal Sesgada y T Sesgada. A partir de un valor fijo de sesgo λ, se grafican las bandas dentro de las cuales deberían caer la mayoría de los puntos si los datos se ajustan a dicha distribución. Se mostrarán las proporciones de puntos por fuera de las bandas, de manera que a menor proporción es mejor el indicador de ajuste a la distribución que se desea probar. Posteriormente se detectará el nivel de sesgo λ que caracterizará la serie de rendimientos bajo la distribución sesgada.
3) Comparación de la distribución Normal Sesgada versus la Normal
El Gráfico 4 muestra las bandas de la Normal Sesgada con λ=0.19, versus las bandas de la Normal, ubicando las observaciones de los rendimientos sobre estas. Para los rendimientos diarios se observa una alta proporción de puntos por fuera de las bandas en la distribución Normal, indicando una falta de ajuste; sin embargo, esta proporción va disminuyendo a medida que el período de rendimientos es mayor, en especial, los rendimientos de 20 días presentan una distribución Normal por tener una muy baja proporción de puntos por fuera de las bandas.
En la Tabla 4 se observa que los rendimientos diarios tienen una alta proporción de puntos por fuera de las bandas normales (90,14%) de las bandas de la distribución Normal Sesgada (90,2%), mostrando que no hay ajuste a ninguna de estas dos distribuciones bajo λ=0,19. Para los rendimientos de 10 días es menor la proporción de puntos por fuera de las bandas de la distribución SN (35,76%) y fuera de las bandas de la Normal (35,76%); sin embargo, esto no refleja un adecuado ajuste a ninguna de estas distribuciones. Los rendimientos de 20 días muestran menor proporción de puntos por fuera de las bandas normales (2,78%), concluyendo dicha distribución como el mejor ajuste para estos rendimientos.
4) Comparación de la distribución T Sesgada vs Normal
Como se aprecia en el Gráfico 5 y en la Tabla 5, para los rendimientos: diario, 5 y 10 días, la proporción de puntos fuera de las bandas de la distribución T Sesgada, con λ = 0,19, es mucho menor que los puntos por fuera de la distribución Normal. Esto da indicios de un mejor ajuste a la T Sesgada que a la Normal Sesgada.
De forma particular, los rendimientos de 20 días presentan igualdad en el ajuste a la distribución T Sesgada y Normal, lo que para efectos financieros tendrá preferencia la segunda distribución en la caracterización de su comportamiento.
5) Algoritmo de búsqueda Tabú
Se presenta el resultado de la búsqueda del nivel de sesgo que minimiza la proporción de puntos por fuera de las bandas de la distribución sesgada respectiva: Normal o T Sesgada, y posteriormente se realiza una comparación entre estas dos distribuciones. Lo anterior se toma como referencia para la selección de la que mejor se ajuste al rendimiento observado.
Se calcularon niveles de sesgo por cada tipo de rendimiento, comenzando por los diarios, en cuyo caso, el algoritmo heurístico arrojó un nivel de λ = 0,0526de la distribución T Sesgada, dejando solo 16,9% de puntos por fuera de las bandas. El Gráfico 6 muestra a la izquierda las bandas de la T Sesgada, que dejan dentro la mayoría de los puntos de estos rendimientos, en comparación con la Normal Sesgada (derecha).Esto muestra una diferencia que permite tomar la decisión sobre un mejor ajuste T Sesgado para los rendimientos diarios.
En la tabla 6 se muestra un resumen de puntos por fuera de las bandas de la ST versus SN con el respectivo parámetro λ estimado en la optimización. Los rendimientos diarios tienen solo 16,94% por fuera de las bandas de ST versus 90,2% de la SN, y los rendimientos de 5 y 10 días tienen 0% para ST vs 58% y 26,7% para SN, respectivamente. Esto muestra que los rendimientos diarios, de 5 y 10 días sí pueden ajustarse mejor a la distribución ST.
En general, la mejor distribución que ajusta los rendimientos diarios, 5 y 10 días, es la T Sesgada, mientras que para los de 20 días es la Normal.
Se evidencia que la prueba propuesta con el algoritmo de optimización presenta más ventajas frente a la existente de Lisi ya que de manera adicional a la detección de la existencia de sesgo, permite caracterizar los rendimientos diarios, de 5 y 10 días con la distribución T Sesgada, y para los de 20 días con la distribución Normal acorde con los resultados de la prueba de normalidad de Jarque Bera.
V. Discusión de resultados
Acorde con los resultados, la detección de dependencia de corto plazo y no normalidad para los rendimientos del IGBC diarios, de 5 y 10 días, y el ajuste que estos últimos presentan con relación a la distribución T Sesgada, permitirían hacer simulaciones de este comportamiento y tomar decisiones a corto, mediano o largo plazo, donde se introduzca tanto la correlación como el sesgo presentes.
Adicional a lo anterior, estos resultados permitirían mejorar la modelación dinámica de los rendimientos bajo esquemas de estimación con la distribución T Sesgada, generando predicciones de estos y, a su vez, estimando los precios futuros para una correcta toma de decisiones.
En el ámbito financiero dicho sesgo detectado permite mejorar la identificación y medición del riesgo en portafolios, mercados y la valoración de activos, al encontrar los desvíos negativos o positivos que puedan presentarse.
Otras implicaciones de estos hallazgos llevan a confirmar la invalidez de los supuestos de normalidad de la Teoría de Mercado de Capitales, como lo exponen diferentes autores (Duran et al., 2013; León & Vivas, 2010; Mandelbrot & Hudson, 2006; Peters, 1994).
Conclusiones
Los resultados muestran que los rendimientos de corto plazo (1, 5 y 10 días) presentan niveles de sesgo que los alejan de una distribución Normal. Dicho de otra forma, el comportamiento que estos presentan no puede ser tratado bajo supuestos normales para efectos de modelación y toma de decisiones. Lo anterior fue comprobado aplicando las dos pruebas presentadas. En la primera (Lisi), se detectó asimetría en los rendimientos de 1, 5, 10 y 20 días. Sin embargo, la prueba de Valencia (2010) detectó sesgos solo en los rendimientos de 1, 5 y 10 días.
Además, de un ajuste adecuado a las distribuciones ST se identificó una distribución Normal o ST para los de 20 días.
Para los rendimientos de 20 días, la prueba de bandas (Valencia, 2010) detecta normalidad, así como la de Jarque Bera acepta la hipótesis de normalidad al 5% de significancia. Sin embargo, no puede descartarse que esta también pueda ser caracterizada con ST. Esto indica, además, mayor confiabilidad sobre la prueba de bandas.
La búsqueda algorítmica del sesgo en los rendimientos resulta ser de gran importancia, ya que permite describir con mayor precisión la forma en que se define la distribución que los caracteriza. Con esta se encontró un nivel de sesgo bajo, que en los rendimientos de corto plazo (1, 5 y 10 días) toman valores de 0,0526, 0,195 y -0,51. Además, al comparar entre las distribuciones Normal, Normal Sesgada y T Sesgada, la que mejor refleja un ajuste es esta última.
NOTAS
1 En: http://www.banrep.gov.co/es/series-estadisticas/see_m_bursatil.htm se podrá encontrar una breve definición conceptual de este índice IGBC.
REFERENCIAS
Arellano-Valle, Reinaldo; Bolfarine, Heleno & Lachos, Víctor (2005). ''Skew-Normal Linear Mixed Models'', Journal of Data Science, Vol. 3, pp. 415–438.
Azzalini, Adelchi (1985). ''A class of distributions which includes the Normal ones'', Scandinavian Journal of Statistics, Vol.12, No. 2, pp. 171–178.
Azzalini, Adelchi & Dalla Valle, Alessandra (1996). ''The Multivariate Skew-Normal Distribution'', Biometrika, Vol.83, No.4, pp. 715–726.
Azzalini, Adelchi & Capitanio, Antonella (1999). ''Statistical applications of the multivariate skew Normal distribution'',Journal of the Royal Statistical Society: Series B, Vol. 61, No. 3, pp. 579–602. Retrieved from http://onlinelibrary.wiley.com/doi/10.1111/1467-9868.00194/abstract (Abril de 2013)
Bolfarine, Heleno; Montenegro, Lourdes & Lachos, Víctor (2007). ''Influence Diagnostics for Skew-Normal Linear Mixed Models'', Sankhya: The Indian Journal of Statistic, Vol. 69, Part. 4, pp. 648–670.
Caicedo, Edinson; Claramunt, Mercé & Casanovas, Monserrat (2011a). ''Teoría actuarial en la cuantificación de las pérdidas por exposición a riesgo de crédito: una aplicación al mercado colombiano'', Academia: Revista Latinoamericana de Administracion, No. 47, pp. 112–125. Recuperado de: http://revistaacademia.uniandes.edu.co/index.php/Cladea/article/viewFile/421/492 (Abril de 2013)
Caicedo, Edinson; Claramunt, Mercé & Casanovas, Monserrat (2011b). ''Medición del riesgo de crédito mediante modelos estructurales: una aplicación al mercado colombiano'', Cuadernos de Administración, Vol. 24, No. 42, pp. 73–100. Recuperado de: http://www.redalyc.org/pdf/205/20520042004.pdf (Abril de 2013).
Chunhachinda, Pornchai; Dandapani, Krishnan; Hamid, Shahid & Prakash, Arun (1997). ''Portfolio selection and skewness: Evidence from international stock markets'', Journal of Banking & Finance,Vol. 21, Issue 2, pp. 143–167. Recuperado de: http://www.sciencedirect.com/science/article/pii/S0378426696000325 (Septiembre de 2013)
Dubova, Irina (2005). ''La validación y aplicabilidad de la teoría de portafolio en el caso colombiano'', Cuadernos de Administración, Vol. 18, No.30, pp. 241–279.
Duran–Vasquez, Rocío; Lorenzo–Valdes, Arturo & Ruiz–Porras, Antonio (2013). ''A GARCH model with autorregresive conditional asymmetry to model time-series: An application to the returns of the Mexican stock market index'', MPRA Paper, No. 46328. Munich Personal RePEc Archive. Recuperado de: http://mpra.ub.uni-muenchen.de/46328/ (Abril de 2013).
Fernández, Horacio (2010a). ''Egarch: un modelo asimétrico para estimar la volatilidad de series financieras'', Revista Ingenierías Universidad de Medellín, Vol. 9, No.16, pp. 49–60.
Fernández, Horacio (2010b). ''Una aplicación del modelo EGARCH para estimar la volatilidad de series financieras'', Revista Ingenierías Universidad de Medellín, Vol. 9, No.17, pp. 95–104. Recuperado de: http://www.redalyc.org/articulo.oa?id=75017164005 (Enero de 2013)
Grajales, Carlos & Pérez, Fredy (2010). ''Valor en riesgo para un portafolio con opciones financieras'', Revista Ingenierías Universidad de Medellín, Vol.9, No. 17, pp. 105–118. Recuperado de: http://www.redalyc.org/pdf/750/75017164014.pdf (Mayo de 2013).
Hull, John (2009). Introducción a los mercados de futuros y opciones (6ta. Ed.). Mexico D.F.:Pearson.
León, Carlos & Vivas, Francisco (2010). ''Dependencia de largo plazo y la regla de la raíz del tiempo para escalar la volatilidad en el mercado colombiano'', Borradores de economía, No. 603. Banco de la República de Colombia.
Lisi, Francesco (2007). ''Testing asymmetry in financial time series'', Quantitative Finance, Vol. 7, Issue 6, pp. 687–696.
Mandelbrot, Benoît & Hudson, Richard (2006). Fractales y finanzas (1a Ed.). Barcelona: Editorial Tusquets
Pérez, Fredy & FernÁndez, Horacio (2006). ''Análisis de la volatilidad del índice general de la bolsa de valores de Colombia utilizando modelos ARCH'', Revista de Ingenierías Universidad de Medellín, Vol. 5, No. 8,pp. 13–33. Recuperado de: http://www.redalyc.org/pdf/750/75050803.pdf (Mayo de 2013)
Peters, Edgar E. (1994). Fractal Market Analysis: Applying Chaos Theory to Investment and Economics. New York: Wiley.
Valencia, Marisol (2010). Estimación en modelos lineales mixtos con datos continuos usando transformaciones y distribuciones no normales. Tesis para optar al título de Magíster en Estadística. Escuela de Estadística. Universidad Nacional de Colombia, Sede Medellín.
Vera, Rocío (2005). ''Reseña de la metodología de construcción de los indicadores más utilizados en Colombia: IPC, IPP, ITCR, IGBC'', Apuntes de Economía, No.6. Recuperado de: http://www.icesi.edu.co/departamentos/economia/publicaciones/docs/Apecon6.pdf (Abril de 2013).
Vernic, Raluca (2005). ''On the multivariate Skew-Normal distribution and its scale mixtures'', An. St. Univ. Ovidius Constanta, Vol. 13, No. 2, pp. 83–96. Recuperado de: http://www.emis.ams.org/journals/ASUO/mathematics/pdf10/83_96_RVernic.pdf (Junio de 2013)