 1) donde
Y = [Y1, ... , Ys]'. Suponga, además, que cada periodo se puede dividir en un
número finito, M , de subperiodos de alta frecuencia.
1) donde
Y = [Y1, ... , Ys]'. Suponga, además, que cada periodo se puede dividir en un
número finito, M , de subperiodos de alta frecuencia.ARTÍCULOS
Desagregación temporal: una metodología multivariada alternativa
Temporal disaggregation: an alternative multivariate methodology
Désagrégation temporelle: une méthodologie multivariée alternative
Jorge Hurtado y Luis Melo*
* Jorge Luis Hurtado Guarín: Profesional del Departamento de Estabilidad Financiera, Banco de la República. Dirección postal: Cra 7 No 14–78 Bogotá, Colombia. Dirección electrónica: jhurtagu@banrep.gov.co
Luis Fernando Melo Velandia: Econometrista principal de la Unidad de Econometría, Banco de la República. Dirección postal: Cra 7 No 14–78 Bogotá, Colombia. Dirección electrónica: lmelovel@banrep.gov.co Los autores agradecen los valiosos comentarios y sugerencias de Eliana González, Daniel Quintero y de dos evaluadores anónimos.
–Introducción. –I. El problema de desagregación temporal. –II. Métodos univariados de desagregación temporal. –III. Métodos multivariados. –IV. Ilustración empírica. –Comentarios finales. –Bibliografía.
Primera versión recibida el 12 de septiembre de 2013; versión final aceptada el 19 de agosto
RESUMEN
En este artículo se propone una nueva extensión de la metodología multivariada de desagregación temporal de Di–Fonzo (1990), la cual supone que los errores de las series de alta frecuencia siguen un modelo VAR(1) en lugar de un proceso ruido blanco. Adicionalmente, se realiza una reseña de diferentes métodos de desagregación, tanto univariados como multivariados, incluyendo sus principales ventajas y desventajas. Finalmente, se lleva a cabo una aplicación multivariada para obtener las cuentas nacionales colombianas mensuales a partir de datos trimestrales. Los resultados bajo la metodología propuesta son similares a los obtenidos por el método de Di–Fonzo, pero son menos volátiles.
Palabras clave: Desagregación temporal, restricciones de agregación temporales y contemporáneas.
Clasificación JEL: C32, C51, E01.
ABSTRACT
In this paper we propose a new extension of Di–Fonzo (1990)'s methodology for multivariate temporal disaggregation. We assume that the errors of the high–frequency series follow a VAR(1) model instead of a white noise process. Additionally, an extensive review of different univariate and multivariate disaggregation methods is presented. Finally, we carry out a multivariate application to obtain Colombia's monthly national accounts from quarterly data. The results obtained using the proposed methodology are similar to those with Di–Fonzo's method. However, our resulting series are less volatile.
Key words: Temporal disaggregation, temporal and contemporaneous aggregation constraints.
JEL Classification: C32, C51, E01.
RÉSUMÉ
Cet article présente une nouvelle extension de la méthodologie désagrégation temporelle multivariée proposée par Di–Fonzo(1990). Cette méthodologie suppose que les erreurs de la série à haute fréquence suivent un modèle VAR(1), au lieu d'un processus bruit blanc. Nous examinons les différentes méthodes de désagrégation aussi bien univariée que multivariée, ainsi que leurs principaux avantages et inconvénients. Enfin, nous avons appliqué la méthodologie multivariée afin d'obtenir les comptes nationaux colombiens mensuels à partir de données trimestrielles. Les résultats obtenus sont similaires à ceux obtenus par la méthode de Di–Fonzo mais ils sont moins volatiles.
Mots clés: désagrégation temporelle, restrictions temporaires, agrégation contemporaine.
Classification JEL: C32, C51, E01.
Introducción
La mayor cantidad de información con la que actualmente se cuenta permite una mayor disponibilidad de datos de alta frecuencia. Sin embargo, todavía existen algunos casos en los que no se cuenta con observaciones de algunas variables a la frecuencia deseada. Un ejemplo típico es el PIB colombiano, que se encuentra disponible en frecuencias trimestrales o anuales, mientras que algunos estudios requieren que sus valores sean mensuales.
La desagregación temporal adquiere relevancia puesto que permite estimar valores de alta frecuencia dadas las observaciones de baja frecuencia. En la literatura se encuentran diferentes métodos de desagregación temporal univariados y multivariados. Algunas de estas metodologías utilizan variables adicionales a la variable de interés para estimar la serie requerida de alta frecuencia. Estas variables son incluidas para tener información de la dinámica de alta frecuencia de la serie a desagregar.
A medida que se cuenta con más información, las estimaciones de las series desagregadas pueden mejorarse. Desde este punto de vista, los métodos multivariados tienen una ventaja sobre los univariados, ya que incluyen un mayor número de datos y relaciones en las metodologías de estimación. En este documento se realiza una nueva extensión de la metodología multivariada de Di–Fonzo (1990), a la vez que se describen algunos métodos de desagregación univariados y multivariados. Adicionalmente, se aplican estas metodologías a las cuentas nacionales colombianas.
El artículo está organizado de la siguiente forma: en la primera sección se define el problema de desagregación temporal y se indican las convenciones de notación que seguirá el artículo. En la segunda sección se describen algunos métodos de desagregación univariados y se discuten sus ventajas y desventajas. En la tercera sección se introducen algunos métodos multivariados, y se propone una extensión a una de estas metodologías. La aplicación de los métodos multivariados se efectúa en la cuarta sección. Por último, se presentan algunos comentarios finales.
I. El problema de desagregación temporal
La desagregación temporal consiste en generar una serie de alta frecuencia, partiendo de la misma en baja frecuencia. Algunos de estos métodos utilizan una o más variables adicionales a la variable de interés, estas variables se denominan variables indicadoras.1 En general, se cuenta con una serie de baja frecuencia que se desea desagregar, de tal forma que la observación de cada periodo se distribuya en una cantidad fija de subperiodos. Por ejemplo, una serie anual observada durante 10 años se podría desagregar para tener 120 observaciones mensuales, lo cual equivale a 12 subperiodos.
Estos métodos de desagregación se pueden clasificar como univariados y multivariados. Los métodos univariados son aquellos en los que hay una única serie a desagregar, mientras que en los multivariados hay más de una serie a desagregar simultáneamente. Adicionalmente, dentro de los métodos univariados y multivariados se pueden encontrar los que usan variables indicadoras y los que no.
Existen tres formas de desagregación temporal que dependen de la naturaleza de la variable que se desea desagregar, estas son: distribución, interpolación y extrapolación. A continuación se describe cada una de ellas.
Cuando se tiene una variable flujo en baja frecuencia, y se quiere desagregar para obtenerla en alta frecuencia, la suma de los valores de los subperiodos de alta frecuencia de cada periodo debe ser igual al valor del periodo correspondiente de baja frecuencia; en este caso se tiene un problema de distribución.
Un problema de interpolación surge cuando se cuenta con una serie de baja frecuencia de una variable stock, observada al inicio o al final del periodo, y se quiere estimar la serie de alta frecuencia de la misma variable. En este caso, si la variable es stock observada al final (inicio) del periodo, se requiere que el valor de la serie estimada de alta frecuencia en el último (primer) subperiodo de cada periodo sea igual a la observada en el periodo correspondiente de la serie de baja frecuencia.
Después de desagregar una serie por distribución o interpolación, en algunas ocasiones se necesita obtener estimaciones que estén por fuera de la muestra observada; en este caso se tiene un problema de extrapolación.
Después de esta breve introducción al problema de desagregación temporal, es necesario formalizar la discusión con el fin de entender en detalle los diferentes métodos. A continuación se presentan las convenciones de notación utilizadas a lo largo del artículo, cuya estructura es similar a la de Di– Fonzo (2002).
A. Notación
Se supone que se ha observado una variable a una frecuencia baja durante
S periodos. Sea Ys la observación de la variable en baja frecuencia en
el periodo s , con s = 1,... , S, y sea Y un vector de dimensión (S  1) donde
Y = [Y1, ... , Ys]'. Suponga, además, que cada periodo se puede dividir en un
número finito, M , de subperiodos de alta frecuencia.
1) donde
Y = [Y1, ... , Ys]'. Suponga, además, que cada periodo se puede dividir en un
número finito, M , de subperiodos de alta frecuencia.
Cuando se utilizan metodologías de desagregación que requieren el uso
de variables indicadoras, se definen wm,s como el vector (1  p) de observaciones
de alta frecuencia de p > 1 variables indicadoras en el periodo s y
subperiodo m, y ws como el vector de las observaciones de baja frecuencia
del mismo conjunto de variables indicadoras en el periodo s, que consiste en
la agregación de wm,s en los subperiodos m = 1, ... , M de s. Adicionalmente,
se define a w como la matriz de dimensión (S
p) de observaciones
de alta frecuencia de p > 1 variables indicadoras en el periodo s y
subperiodo m, y ws como el vector de las observaciones de baja frecuencia
del mismo conjunto de variables indicadoras en el periodo s, que consiste en
la agregación de wm,s en los subperiodos m = 1, ... , M de s. Adicionalmente,
se define a w como la matriz de dimensión (S  p) que contiene las observaciones
de baja frecuencia de todos los periodos de las p variables indicadoras.
Por otro lado, si wh = [w1h ,..., wNh]' es el vector de observaciones de baja frecuencia
de la variable indicadora h, con h = 1, ... , p, entonces w = [w1 , ... , wp ]
es la matriz de dimensión (N
p) que contiene las observaciones
de baja frecuencia de todos los periodos de las p variables indicadoras.
Por otro lado, si wh = [w1h ,..., wNh]' es el vector de observaciones de baja frecuencia
de la variable indicadora h, con h = 1, ... , p, entonces w = [w1 , ... , wp ]
es la matriz de dimensión (N  p) que contiene todas las observaciones de
alta frecuencia de las p variables indicadoras en N subperiodos, con N > M S.
p) que contiene todas las observaciones de
alta frecuencia de las p variables indicadoras en N subperiodos, con N > M S.
A partir de los datos observados Y y w, se busca estimar los valores ym,s
que corresponden a los valores no observados de alta frecuencia en el subperiodo
m del periodo s de la variable de interés. Sean y = [y1, ... , yN]' y 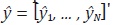 los vectores de dimensión (N
los vectores de dimensión (N  1)2 que contienen los valores no
observados de alta frecuencia y los valores estimados de alta frecuencia de la
variable de interés, respectivamente. En algunos métodos se utiliza un estimador
preliminar de y, que se nota como y tiene la misma dimensión que
1)2 que contienen los valores no
observados de alta frecuencia y los valores estimados de alta frecuencia de la
variable de interés, respectivamente. En algunos métodos se utiliza un estimador
preliminar de y, que se nota como y tiene la misma dimensión que 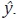 .
.
Como se explicó al inicio de la sección, dependiendo de la naturaleza
de la variable las condiciones del problema de desagregación cambian. En
particular, la restricción de agregación es distinta si la variable a desagregar es un
flujo, un stock o un promedio. Sea c un vector de dimensión M  1, de tal
forma que al premultiplicar los valores de los subperiodos de un periodo
determinado por dicho vector, se obtiene la observación de baja frecuencia
correspondiente. Entonces se define la restricción de agregación para el
periodo s como:
1, de tal
forma que al premultiplicar los valores de los subperiodos de un periodo
determinado por dicho vector, se obtiene la observación de baja frecuencia
correspondiente. Entonces se define la restricción de agregación para el
periodo s como:

donde c' = [c1, ... , cM] es un vector de M constantes conocidas. Si Ys representa un flujo, c' = [1,1, ... ,1]; si Ys es un promedio, c' = [1/M, 1/M, ... , 1/M]; si es un stock observado al final del periodo, c' = [0,0, ... ,1], y si es un stock observado al inicio del periodo, c' = [1,0, ... ,0]. Los primeros dos casos corresponden al problema de distribución, y los dos últimos corresponden al de interpolación. Por lo tanto, la restricción de agregación para el periodo s puede tomar las siguientes formas:
Distribución:
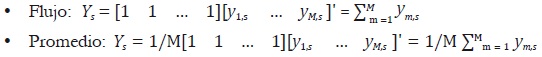
Interpolación:
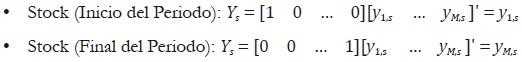
Es conveniente definir el conjunto de restricciones de agregación de
todos los periodos, con el fin de asociar la restricción de agregación a los
vectores Y y y. Sea C1 la siguiente matriz de dimensión S  MS:
MS:

donde IS es una matriz identidad de orden s. Para los problemas de distribución e interpolación sin extrapolación, el conjunto de restricciones de agregación se define como Y = C1 y. En el caso de extrapolación a un horizonte r, el conjunto de restricciones de agregación es:

donde C2 = C1|0r es la matriz formada por la unión (por columnas) de las
matrices C1 y 0r, siendo esta última una matriz de ceros de dimensión
M  r.3 La matriz de ceros se incluye porque cuando se asocia un problema de
extrapolación los valores de alta frecuencia estimados por fuera de la muestra
no están sujetos a la restricción de agregación.
r.3 La matriz de ceros se incluye porque cuando se asocia un problema de
extrapolación los valores de alta frecuencia estimados por fuera de la muestra
no están sujetos a la restricción de agregación.
Para simplificar la notación, se define C como la matriz de agregación, que será igual a C1 si se tiene un problema de distribución o interpolación sin extrapolación, y será igual a C2 si se tiene un problema de extrapolación. Dado lo anterior, el conjunto de restricciones de agregación es:

Teniendo en cuenta las anteriores convenciones de notación, en la siguiente sección se explican algunos métodos de desagregación.
II. Métodos univariados de desagregación temporal
En esta sección se hace una reseña de algunos de los métodos univariados de desagregación temporal más utilizados en la literatura. Adicionalmente, se discuten sus ventajas y desventajas. En la Tabla 1 se resumen las características principales de estos métodos.
A. Método de Denton (1971)
El objetivo del artículo de Denton (1971) es encontrar la forma de ajustar series preliminares (observadas) mensuales o trimestrales para que coincidan con agregados o promedios anuales de fuentes independientes. Este método no permite extrapolación, ya que exige que N = MS.
El método busca estimar una serie de alta frecuencia 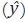 a partir de una
serie preliminar observada
a partir de una
serie preliminar observada 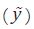 de la misma frecuencia, utilizando restricciones
de agregación dadas por la serie observada de baja frecuencia (Y).
de la misma frecuencia, utilizando restricciones
de agregación dadas por la serie observada de baja frecuencia (Y).
El problema consiste en minimizar la siguiente función de pérdida, 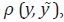 sujeta a la restricción de agregación:
sujeta a la restricción de agregación:
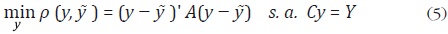
donde A es una matriz simétrica de dimensión MS  MS cuya forma se especificará
más adelante. El lagrangiano asociado a la expresión (5) es:
MS cuya forma se especificará
más adelante. El lagrangiano asociado a la expresión (5) es:
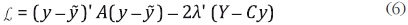
con λ' = [λ1, λ2, ... , λS]. Derivando (6) con respecto a y y λ, e igualando a cero, se obtiene:
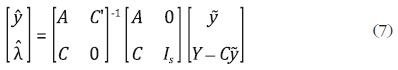
donde IS es la matriz identidad de orden S. Resolviendo para 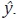 , se tiene el
siguiente resultado:
, se tiene el
siguiente resultado:
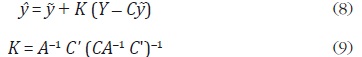
La ecuación (8) muestra que la estimación de y es una combinación lineal
entre la serie preliminar 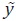 y la discrepancia entre las agregaciones de la serie
preliminar C
y la discrepancia entre las agregaciones de la serie
preliminar C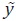 y la serie agregada Y. Es decir, la estimación preliminar se ajusta
distribuyendo la discrepancia agregada de acuerdo a la matriz de ponderaciones
K. Sin embargo, K depende de A, por lo que se debe tener una forma
explícita de A con el fin de realizar la estimación.
y la serie agregada Y. Es decir, la estimación preliminar se ajusta
distribuyendo la discrepancia agregada de acuerdo a la matriz de ponderaciones
K. Sin embargo, K depende de A, por lo que se debe tener una forma
explícita de A con el fin de realizar la estimación.
Una primera alternativa es definir A = IMS , caso en el cual la función de pérdida es la suma de los cuadrados de las diferencias entre la serie preliminar y la serie a estimar, lo que implica que la discrepancia se está distribuyendo en montos iguales entre los M subperiodos.
Denton propone una especificación alterna de A, de tal forma que la
función de pérdida sea la suma de los cuadrados de las d –ésimas diferencias
de 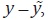 es decir,
es decir, 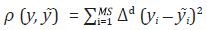 . Para obtener matricialmente
esta función, es necesario definir primero la siguiente matriz D de dimensión
MS
. Para obtener matricialmente
esta función, es necesario definir primero la siguiente matriz D de dimensión
MS  MS:
MS:
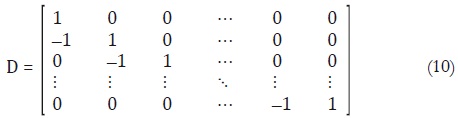
de esta manera:
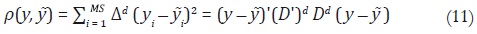
Como señala Denton, la matriz D simplifica el cálculo de la inversa de A.
Sin embargo, el método tiene algunas debilidades, la principal es que la función
de pérdida se minimiza en cero, lo que implica que 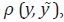 es mínima
cuando
es mínima
cuando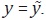 Dicha condición es una restricción importante, porque implica
que en el punto óptimo la estimación preliminar y la estimación final deben
ser iguales. Por otro lado, el método no tiene en cuenta las características estocásticas
de las series preliminar y final, como el orden de integración, o si
existe una relación de cointegración entre estas series.
Dicha condición es una restricción importante, porque implica
que en el punto óptimo la estimación preliminar y la estimación final deben
ser iguales. Por otro lado, el método no tiene en cuenta las características estocásticas
de las series preliminar y final, como el orden de integración, o si
existe una relación de cointegración entre estas series.
B. Método de Chow y Lin (1971)
A diferencia del método de Denton (1971), Chow y Lin (1971) resuelven el problema de desagregación temporal encontrando el mejor estimador lineal insesgado (MELI) de la serie a estimar, y. Una ventaja de este método con respecto al de Denton, es que éste sí permite extrapolar.
Para obtener el mejor estimador lineal insesgado de y, Chow y Lin suponen que existe una relación lineal entre la serie a estimar (y) y las p series indicadoras (w) en alta frecuencia:

donde y y w son el vector y la matriz definidas en la sección anterior, β es
un vector de coeficientes de dimensión p  1, y u es un proceso i.i.d. de dimensión N
1, y u es un proceso i.i.d. de dimensión N  1 con media cero y matriz de covarianzas V. Si se premultiplica
la ecuación (12) por la matriz de agregación C, se obtiene el modelo de baja
frecuencia:
1 con media cero y matriz de covarianzas V. Si se premultiplica
la ecuación (12) por la matriz de agregación C, se obtiene el modelo de baja
frecuencia:
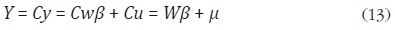
donde µ = Cu con E(µµ' ) = CVC' . Chow y Lin muestran que el mejor estimador lineal (MELI) de y está dado por:
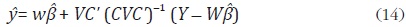
donde 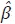 es el estimador de mínimos cuadrados generalizados del modelo
(13), el cual tiene la siguiente forma:
es el estimador de mínimos cuadrados generalizados del modelo
(13), el cual tiene la siguiente forma:
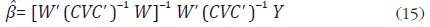
En el caso más sencillo, se supone que los errores de alta frecuencia son ruido blanco con varianza σ2, lo que implica que V = σ2 IN. Con esta especificación, la discrepancia agregada de cada periodo (residuales de la ecuación (14)) se asigna en partes iguales para cada subperiodo en el caso de distribución. En el caso de interpolación con variable observada al inicio (final) del periodo, la discrepancia agregada de cada periodo se asigna al primer (último) subperiodo de dicho periodo.
Dadas las limitaciones de la especificación de ruido blanco en los errores de alta frecuencia, Chow y Lin suponen, de forma alterna, que los errores siguen un proceso autorregresivo de orden uno, AR(1), en el cual:
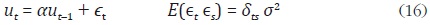
donde εt es un proceso ruido blanco con varianza σ2. Adicionalmente, | α | < 1, por consiguiente la matriz de covarianzas está definida de la siguiente forma:
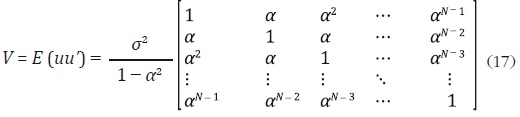
Debido a que V está en función de α y σ2, la estimación de la matriz
de covarianzas implica la estimación de estos parámetros. Chow y Lin proponen
un método iterativo para estimar α, pero solo lo desarrollan para el
caso de la desagregación de series trimestrales a mensuales. Autores como
Barcellan (2002) y Lupi y Parigi (2002) señalan que si se supone que los
errores de alta frecuencia siguen una distribución normal, entonces se pueden
estimar β, α y σ2 utilizando el método de máxima verosimilitud. Estos
autores mencionan un método alterno para estima α , el cual consiste en
minimizar 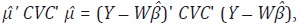 respecto a α. La estimación
de α se hace a través de una búsqueda por rejilla (grid search) en el que
se asignan valores de α entre –1 y 1, y se escoge el valor que maximice la
función de verosimilitud logarítmica.4
respecto a α. La estimación
de α se hace a través de una búsqueda por rejilla (grid search) en el que
se asignan valores de α entre –1 y 1, y se escoge el valor que maximice la
función de verosimilitud logarítmica.4
Aunque el método de Chow y Lin tiene un enfoque diferente al de Denton, las soluciones de ambos métodos tienen una estructura similar. Los dos métodos obtienen una solución que se puede expresar como una combinación lineal entre la discrepancia agregada y una proxy de la variable a estimar. Además, en ambos casos la solución depende de una función objetivo que se puede expresar como una forma cuadrática que depende de una matriz desconocida (A en el caso de Denton y V en el caso de Chow y Lin).
La principal desventaja del método de Chow y Lin es que solo suponen dos procesos muy simples para los errores de alta frecuencia, ruido blanco y AR(1).
C. Método de Fernández (1981)
Dada la relación que parece existir entre los métodos de Denton (1971) y Chow y Lin (1971), Fernández (1981) propone un método de desagregación que consiste en una reformulación de método de Denton en el contexto de estimación óptima, tratado por Chow y Lin. En principio, Fernández generaliza el método de Denton, y encuentra los supuestos adicionales para que las soluciones de Denton y de Chow y Lin sean equivalentes. Lo anterior implica que la solución de Fernández se puede expresar como un estimador MELI de y, y que además dicha estimación no daría lugar a una serie con discontinuidades artificiales.
Para generalizar el método de Denton, Fernández propone el siguiente problema de minimización:
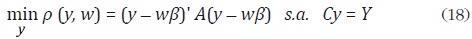
Al igual que en los casos anteriores, la función de pérdida dada en (18) corresponde a una forma cuadrática. Como caso particular, cuando β = 1 se obtiene la función objetivo de Denton. Fernández muestra que la solución a este problema de minimización está dada por:
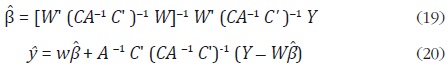
Es importante notar que la expresión (20) es equivalente a (8) cuando β = 1 y w = 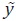 . Si A = IN , la ecuación (18) corresponde a la suma de los errores al cuadrado, la cual equivale a la función objetivo del método de mínimos
cuadrados usado en los modelos de regresión lineal. Si se mantienen
los supuestos tradicionales sobre el término de error y A = IN, la solución a
(18) es un estimador MELI de y.
. Si A = IN , la ecuación (18) corresponde a la suma de los errores al cuadrado, la cual equivale a la función objetivo del método de mínimos
cuadrados usado en los modelos de regresión lineal. Si se mantienen
los supuestos tradicionales sobre el término de error y A = IN, la solución a
(18) es un estimador MELI de y.
No obstante, existe otra forma de relacionar los enfoques de minimización de función de pérdida cuadrática y MELI. Para mostrar este punto, Fernández supone que existe una relación lineal similar a (12), donde sus errores siguen una caminata aleatoria, es decir:

Adicionalmente, se supone que las innovaciones de (21), εt , siguen un proceso ruido blanco con media cero y varianza σ2. También se asume que u0 = 0, de tal forma que Var(u1) = σ2. Tomando primeras diferencias de (12) y utilizando la matriz D definida en (10), se obtiene el siguiente modelo:

donde E(Duu' D') = σ2 IN . Fernández anota que transformar el modelo (22) a baja frecuencia, es decir premultiplicándolo por C, no es útil porque la agregación de las primeras diferencias de las variables flujo no es una magnitud observable. Por esta razón realiza una transformación adicional en la cual relaciona la primera diferencia en baja frecuencia con la primera diferencia en alta frecuencia, y muestra que el mejor estimador lineal de y, dados los supuestos anteriores, es de la forma:
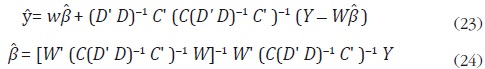
Las expresiones (20) y (23) son idénticas cuando A = D' D, lo que implica que en este caso el enfoque de minimización de pérdida cuadrática tiene una solución que es equivalente al MELI de y.
El método de Fernández proporciona un marco formal al enfoque de minimización de una función de pérdida planteado por Denton (1971), al incluir supuestos que lo relacionan con estimadores de un modelo de regresión lineal. Además, Fernández evita el problema de la estimación de parámetros adicionales (como α en el método de Chow y Lin), al suponer una caminata aleatoria en los errores.
Sin embargo, el supuesto de la caminata aleatoria sobre los errores de (12) implica que las series de alta frecuencia (y y w) no pueden estar cointegradas, lo cual es una restricción importante en la práctica.
D. Método de Litterman (1983)
Litterman (1983) desarrolla un método que busca generalizar el propuesto por Fernández (1981). Litterman supone la existencia de una relación lineal entre la serie a estimar y un conjunto de series indicadoras. Esta relación equivale a la ecuación (12) de la metodología de Chow y Lin.
Este autor propone que los errores de (12), siguen el proceso:
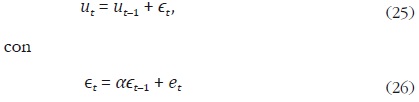
donde et es un proceso ruido blanco con varianza σ2. Es decir, Litterman conserva el supuesto de caminata aleatoria de Fernández, como se muestra en la ecuación (25). Sin embargo, no supone que el error de (12) es un proceso ruido blanco.
De las expresiones (25) y (26) se sigue que:
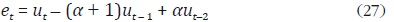
En forma vectorial:

donde e = [e1, ..., eN], D es la matriz definida en (10), y
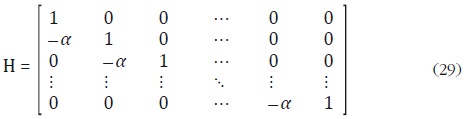
La ecuación (28) implica que el vector de errores de alta frecuencia u tiene la siguiente forma:

Por lo tanto, la varianza de u es:
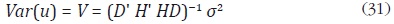
La solución de Litterman se obtiene al sustituir (31) en la solución de Chow y Lin dada en la expresión (14):
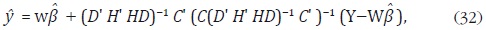
donde
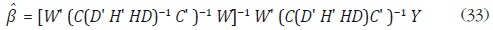
Las expresiones (32) y (33) dependen de la matriz H, que a su vez depende del parámetro α. Litterman propone un método para estimar α, pero solo es aplicable a la desagregación de series trimestrales a mensuales.
Aunque Litterman generaliza el enfoque de Fernández (1981), éste no
supera su problema principal, ya que no admite la existencia de relaciones
de cointegración entre yt y wt. Para probar lo anterior, observe que los
supuestos sobre uτ implican que 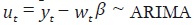 (1,1,0) y, por lo
tanto, (1, – β')' no se puede interpretar como un vector de cointegración,
debido a que ut es integrada de orden uno. Por otro lado, el autor no desarrolla
un método para estimar el parámetro α para cualquier frecuencia de
los datos.
(1,1,0) y, por lo
tanto, (1, – β')' no se puede interpretar como un vector de cointegración,
debido a que ut es integrada de orden uno. Por otro lado, el autor no desarrolla
un método para estimar el parámetro α para cualquier frecuencia de
los datos.
E. Método de Guerrero (1990)
El método de Guerrero (1990), al igual que los métodos de Chow y Lin (1971), Fernández (1981) y Litterman (1983), parte de la existencia de una relación lineal de las variables de alta frecuencia. Además, su enfoque se centra en la estructura que sigue la variable y, y no en la de los errores de alta frecuencia de la ecuación (12). De la misma forma que el método de Denton (1971), el método de Guerrero (1990) requiere una estimación preliminar de la variable de interés con el fin de estimar la serie de alta frecuencia.
Para resolver el problema de desagregación, Guerrero supone que la serie de alta frecuencia no observada, yt, sigue un proceso ARIMA:
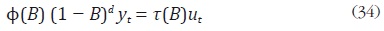
donde B es el operador de rezago, Φ(B) y τ(B) son polinomios de rezagos de
orden finito con coeficientes conocidos, d indica el grado de diferenciación
de yt , y ut es un proceso ruido blanco con varianza 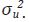 Dada esta estructura,
el estimador lineal de mínimo error cuadrático medio de yt, basado en información
hasta el periodo 0, está dado por:
Dada esta estructura,
el estimador lineal de mínimo error cuadrático medio de yt, basado en información
hasta el periodo 0, está dado por:
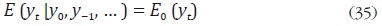
El error de pronóstico es:
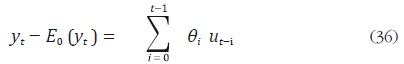
donde 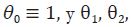 ... son los coeficientes del polinomio
... son los coeficientes del polinomio 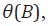 tales que
tales que
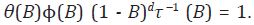 La representación matricial de la expresión
(36) es:
La representación matricial de la expresión
(36) es:

donde θ es una matriz triangular inferior formada por la secuencia 1, θ1, ..., θN – 1 en la primera columna, 0,1,θ1, ... ,θN – 2 en la segunda columna, y así sucesivamente. u es un vector aleatorio con E0 (u) = 0, y E0 (uu') = σu2IN. Al incorporar el conjunto de restricciones de agregación, Y = Cy, Guerrero muestra que la solución al problema de desagregación está dada por:
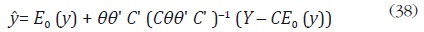
En la práctica, se debe estimar E0 (y). Para tal fin, Guerrero supone que
existe una estimación preliminar de y, 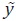 , que debe satisfacer los siguientes
supuestos:
, que debe satisfacer los siguientes
supuestos:

Dados estos supuestos, el valor esperado de la expresión (37), condicionado
a 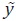 , es:
, es:
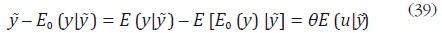
Substrayendo (39) de (37), se llega a la siguiente expresión:

donde ω = u – E(u| 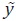 ) es un vector aleatorio con E(ω|
) es un vector aleatorio con E(ω| 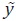 ) = 0 y
E(ωω' |
) = 0 y
E(ωω' | 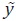 ) = σ2 P, con P una matriz definida positiva. Como resultado del
primer supuesto, y notando la similitud de las expresiones (37) y (40), un estimador
MELI de y está dado por:
) = σ2 P, con P una matriz definida positiva. Como resultado del
primer supuesto, y notando la similitud de las expresiones (37) y (40), un estimador
MELI de y está dado por:
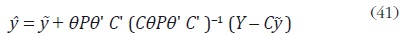
con
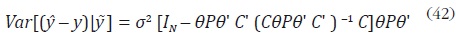
Sin embargo, la estimación final de y depende de σ2 y P, que son desconocidos. Guerrero sugiere el siguiente procedimiento para estimar σ2 y P:
Inicialmente, se supone P = IN y se calcula 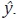 en la expresión (41). Posteriormente,
se construye la serie
en la expresión (41). Posteriormente,
se construye la serie 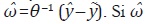 es ruido blanco, entonces el supuesto P = IN se acepta; por lo tanto,
es ruido blanco, entonces el supuesto P = IN se acepta; por lo tanto, 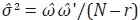 es un estimador
apropiado de σ2, donde r es el número de parámetros estimados en el modelo
ARIMA de
es un estimador
apropiado de σ2, donde r es el número de parámetros estimados en el modelo
ARIMA de 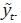 En el caso de que
En el caso de que 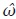 no sea ruido blanco, se debe construir
un modelo ARIMA sobre
no sea ruido blanco, se debe construir
un modelo ARIMA sobre 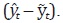 Con base en este resultado, se obtiene un
estimador de la matriz Ω que satisface la expresión e = Qω = Qθ –1 (y –
Con base en este resultado, se obtiene un
estimador de la matriz Ω que satisface la expresión e = Qω = Qθ –1 (y – 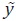 ) =
Ω–1 (y –
) =
Ω–1 (y – 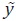 ), tal que QPQ' = IN.
), tal que QPQ' = IN.
Finalmente, se estima y a partir de (41) teniendo en cuenta que ΩΩ' =
θ(Q' Q)– 1 θ' = θPθ'. Adicionalmente, se calcula la matriz de covarianzas dada
en la expresión (42), donde el estimador de σ2 está dado por 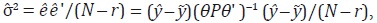 con N – r los grados de libertad del modelo
ARIMA correspondiente.
con N – r los grados de libertad del modelo
ARIMA correspondiente.
En el método de Guerrero, al igual que en el de Denton, la estimación
final de la serie desagregada depende de una estimación preliminar de dicha
serie. Una ventaja de este método, a diferencia del de Denton, es que se proporciona
una metodología para obtener 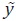 ̃. Guerrero propone una estimación
preliminar a partir de un conjunto de series indicadoras, w, la cual tiene la
siguiente forma:
̃. Guerrero propone una estimación
preliminar a partir de un conjunto de series indicadoras, w, la cual tiene la
siguiente forma:

Al sustituir (43) en la versión agregada de (40), se obtiene el siguiente resultado:
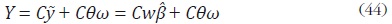
La expresión anterior se puede notar de la siguiente forma:

donde ε = Cθω. Por lo tanto, 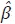 puede ser obtenido utilizando mínimos
cuadrados ordinarios sobre (45).
puede ser obtenido utilizando mínimos
cuadrados ordinarios sobre (45).
Otra ventaja del método de Guerrero (1990), en comparación con los métodos de Chow y Lin (1971), Fernández (1981) y Litterman (1983), es que no requiere realizar supuestos sobre los errores de alta frecuencia.
Como lo señalan Lupi y Parigi (2002), una de las críticas al método de
Guerrero es que éste no se puede aplicar cuando existe una relación de cointegración entre la serie preliminar y la serie no observada de alta frecuencia.
Para ilustrar este punto, considere que 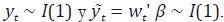 Dados
los supuestos iniciales de Guerrero, se tiene que las dos series siguen la misma
representación ARIMA, de modo que:
Dados
los supuestos iniciales de Guerrero, se tiene que las dos series siguen la misma
representación ARIMA, de modo que:
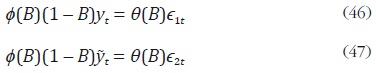
donde φ(B) y φ(B) son dos polinomios de rezagos de orden finito cuyos
coeficientes son conocidos, y ε1t y ε2t son dos procesos ruido blanco ortogonales
con varianza 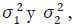 respectivamente. Al realizar una combinación
lineal entre (46) y (47), se tiene la siguiente expresión:
respectivamente. Al realizar una combinación
lineal entre (46) y (47), se tiene la siguiente expresión:
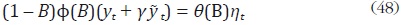
donde 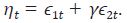 De (48) se puede concluir que la combinación lineal
entre las series desagregadas no es estacionaria y, por lo tanto, las dos series
no pueden estar cointegradas.
De (48) se puede concluir que la combinación lineal
entre las series desagregadas no es estacionaria y, por lo tanto, las dos series
no pueden estar cointegradas.
Por otro lado, si se supone que yt y 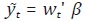 son generados por el
siguiente proceso bivariado:
son generados por el
siguiente proceso bivariado:

donde θ11 (B) y θ22 (B) son dos polinomios de rezagos con coeficientes conocidos.
La primera ecuación del sistema (49) implica que las dos series están
cointegradas, donde el vector de cointegración es [1, –δ]', mientras que la
segunda ecuación implica que 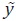 t es I(1).
t es I(1).
Se puede mostrar que si θ11 (B) ≡ 1 y Δ ≡ 1, entonces Δyt = Δε1t + θ22
(B)ε2t , lo que implica que yt y 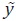 t no pueden ser generados por el mismo proceso
ARIMA. En resumen, se puede mostrar que si la serie preliminar y la
variable de interés siguen el mismo proceso ARIMA no pueden estar cointegradas,
y que si se parte de que están cointegradas no necesariamente siguen
el mismo proceso ARIMA.
t no pueden ser generados por el mismo proceso
ARIMA. En resumen, se puede mostrar que si la serie preliminar y la
variable de interés siguen el mismo proceso ARIMA no pueden estar cointegradas,
y que si se parte de que están cointegradas no necesariamente siguen
el mismo proceso ARIMA.
F. Método de Santos–Silva y Cardoso (2001)
Al igual que Guerrero (1990), Santos–Silva y Cardoso (2001) proponen un método que supone una estructura sobre las variables de alta frecuencia, y no sobre los errores asociados a la relación lineal entre dichas variables. A diferencia de los métodos de Chow y Lin (1971), Fernández (1981) y Litterman (1983), que proponen un modelo lineal estático para las series de alta frecuencia –ecuación (12)–, Santos–Silva y Cardoso (2001) proponen el siguiente modelo lineal dinámico:

donde |k| < 1 y vt es un proceso ruido blanco. Como lo señalan los autores, este método puede ser utilizado incluyendo rezagos adicionales de yt y rezagos de las variables indicadoras en el vector wt . Asumiendo |k| < 1, y realizando sustituciones recursivas, el modelo (50) puede escribirse como:
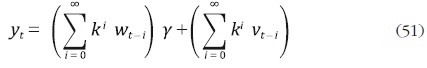
La ecuación (51) puede expresarse como:
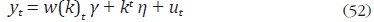
donde 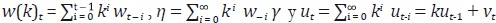 es
un error estacionario que sigue un proceso AR(1).
es
un error estacionario que sigue un proceso AR(1).
La ecuación (52) se puede expresar en forma vectorial como:

Premultiplicando (53) por la matriz de agregación C, se obtiene:

Nótese que y depende de los parámetros k, η y γ. Como se puede apreciar
en la ecuación (52), esta dependencia es lineal en η y γ , pero no en k. Por
consiguiente, si se parte de un estimador de k, 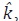 , los estimadores de η y γ pueden
ser obtenidos mediante el método de mínimos cuadrados generalizados
sobre la ecuación (55). Adicionalmente, Santos Silva y Cardoso muestran que
un estimador de la serie desagregada es:
, los estimadores de η y γ pueden
ser obtenidos mediante el método de mínimos cuadrados generalizados
sobre la ecuación (55). Adicionalmente, Santos Silva y Cardoso muestran que
un estimador de la serie desagregada es:
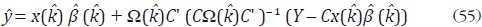
donde 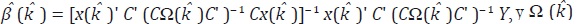 es la matriz de covarianzas de u condicionada a
es la matriz de covarianzas de u condicionada a 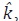 con u0 = 0. Los
autores sugieren estimar k mediante el método de máxima verosimilitud.
con u0 = 0. Los
autores sugieren estimar k mediante el método de máxima verosimilitud.
Una de las ventajas del método de Santos–Silva y Cardoso es que supone una estructura sobre las series desagregadas y no sobre los errores asociados a los modelos de alta frecuencia. Adicionalmente, en contraste al método de Guerrero, este método es válido cuando existen relaciones de cointegración entre las variables de alta frecuencia. Los autores afirman que el modelo dinámico que ellos proponen se puede expresar como un modelo de corrección de errores.
III. Métodos multivariados
En esta sección se hace una reseña de algunos de los métodos multivariados de desagregación temporal y se propone una nueva extensión del método de Di–Fonzo (1990). En la Tabla 2 se resumen las características principales de estos métodos.
A. Método de Rossi (1982)
Rossi (1982) generaliza el método de Chow y Lin (1971) al caso multivariado.
Este método parte de una matriz de dimensión S  H de series
agregadas Y = [Y1, ... , YH], donde Yh es un vector de dimensión S
H de series
agregadas Y = [Y1, ... , YH], donde Yh es un vector de dimensión S  1 que
contiene los valores de baja frecuencia de la serie h, con h = 1, ... , H. El
problema consiste en estimar la matriz de dimensión N
1 que
contiene los valores de baja frecuencia de la serie h, con h = 1, ... , H. El
problema consiste en estimar la matriz de dimensión N  H, y = [y1, ... , yH], que contiene las series de alta frecuencia correspondientes. Al igual que las
metodologías descritas en las secciones anteriores, Rossi supone que existe la
siguiente relación:
H, y = [y1, ... , yH], que contiene las series de alta frecuencia correspondientes. Al igual que las
metodologías descritas en las secciones anteriores, Rossi supone que existe la
siguiente relación:

donde y = vec(y) es un vector de dimensión NH  1 obtenido al aplicar el
operador vec(·) a la matriz y.5 La matriz w es una matriz diagonal en bloques
de dimensión NH
1 obtenido al aplicar el
operador vec(·) a la matriz y.5 La matriz w es una matriz diagonal en bloques
de dimensión NH  p definida como:
p definida como:
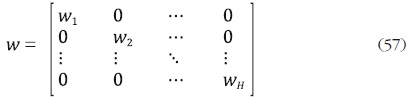
donde wh es una matriz N  ph de variables indicadoras asociadas a la variable
h con h = 1, ... H. Por otro lado, β es un vector de parámetros de dimensión
ph de variables indicadoras asociadas a la variable
h con h = 1, ... H. Por otro lado, β es un vector de parámetros de dimensión 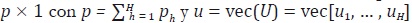 es un proceso ruido
blanco multivariado con
es un proceso ruido
blanco multivariado con 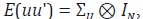 donde ΣU es una matriz definida
positiva de dimensión H
donde ΣU es una matriz definida
positiva de dimensión H  H.
H.
Debido a su carácter multivariado, este método tiene la ventaja de considerar dos tipos de restricciones de agregación. La primera corresponde a la restricción de agregación temporal, similar a la expuesta en los métodos univariados. La segunda se relaciona con una restricción de agregación contemporánea.
Rossi define la agregación contemporánea de y como el vector z = yjH,
donde jH es un vector de unos de dimensión H 1. El método supone que z
es conocido. Si se define
1. El método supone que z
es conocido. Si se define 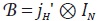 como la matriz de agregación contemporánea,
entonces la ecuación que resulta de premultiplicar (56) por
como la matriz de agregación contemporánea,
entonces la ecuación que resulta de premultiplicar (56) por 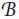 es:
es:

Rossi muestra que el mejor estimador lineal insesgado de y está dado por:
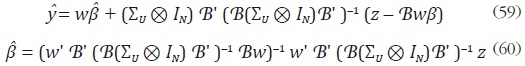
Es importante anotar que 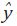 satisface la restricción de agregación contemporánea,
es decir,
satisface la restricción de agregación contemporánea,
es decir, 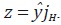 Sin embargo, no se garantiza que las restricciones
de agregación temporal se satisfagan. Para imponer estas restricciones, se
define la matriz de agregación temporal
Sin embargo, no se garantiza que las restricciones
de agregación temporal se satisfagan. Para imponer estas restricciones, se
define la matriz de agregación temporal 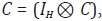 donde C es la matriz
de agregación temporal definida en (2). De esta forma, el conjunto de restricciones
de agregación temporales del caso multivariado está dado por Cy = Y,
donde Y = vec(Y). En este caso, se puede probar que no se satisface
donde C es la matriz
de agregación temporal definida en (2). De esta forma, el conjunto de restricciones
de agregación temporales del caso multivariado está dado por Cy = Y,
donde Y = vec(Y). En este caso, se puede probar que no se satisface 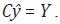 Por esta razón, Rossi redefine la matriz w tal que:
Por esta razón, Rossi redefine la matriz w tal que:
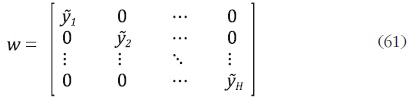
donde 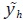 es el mejor estimador lineal insesgado de yh –dado en (14)–, aplicando
el método univariado de Chow y Lin (1971)6 para la variable h y sus
variables indicadoras asociadas wh , con h = 1, ... , H. Si se reemplaza la matriz
w definida en (61) en (59) y (60) se puede probar que
es el mejor estimador lineal insesgado de yh –dado en (14)–, aplicando
el método univariado de Chow y Lin (1971)6 para la variable h y sus
variables indicadoras asociadas wh , con h = 1, ... , H. Si se reemplaza la matriz
w definida en (61) en (59) y (60) se puede probar que 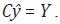 es decir,
que se garantiza que el estimador satisface tanto la restricción de agregación
contemporánea como las restricciones temporales.
es decir,
que se garantiza que el estimador satisface tanto la restricción de agregación
contemporánea como las restricciones temporales.
Para encontrar la matriz ΣU se debe suponer alguna estructura en los
errores de (56), el caso más sencillo es  por lo cual
por lo cual 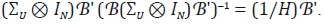 Por lo tanto,
Por lo tanto, 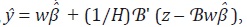 es decir, la discrepancia
es decir, la discrepancia 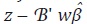 se reparte en partes iguales entre las H variables.
se reparte en partes iguales entre las H variables.
Rossi describe un caso alternativo en el que la matriz ΣU es diagonal,
donde el elemento hh de esta matriz, σU,hh, se supone proporcional a la media
del indicador 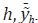 En este caso
En este caso 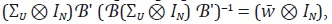 donde
donde 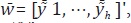 lo que significa que la discrepancia se distribuye de
forma proporcional.
lo que significa que la discrepancia se distribuye de
forma proporcional.
Una de las desventajas del método de Rossi es que no considera el caso
de extrapolación. Otra desventaja de este método es que al suponer que
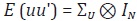 se tiene que E (uh uk') = σhk IN con h, k = 1, ... , H. Esta restricción
constituye un supuesto fuerte, ya que implica que no pueden existir
estructuras de heteroscedasticidad ni autocorrelación en el tiempo.
se tiene que E (uh uk') = σhk IN con h, k = 1, ... , H. Esta restricción
constituye un supuesto fuerte, ya que implica que no pueden existir
estructuras de heteroscedasticidad ni autocorrelación en el tiempo.
Di–Fonzo (1990) muestra que 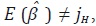 dado que los regresores del
modelo (58) son estocásticos.7 Lo anterior implica que
dado que los regresores del
modelo (58) son estocásticos.7 Lo anterior implica que 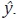 será consistente
con z pero no con Y, es decir, no se cumplen las restricciones de agregación
temporales, ya que se tiene
será consistente
con z pero no con Y, es decir, no se cumplen las restricciones de agregación
temporales, ya que se tiene 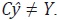 Bajo el esquema propuesto por Rossi, la
única forma posible para que se cumplan las restricciones contemporáneas y
temporales simultáneamente es reemplazando
Bajo el esquema propuesto por Rossi, la
única forma posible para que se cumplan las restricciones contemporáneas y
temporales simultáneamente es reemplazando 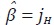 en (60). Este resultado
se puede interpretar como una generalización del método univariado de Denton
(1971) al caso multivariado.
en (60). Este resultado
se puede interpretar como una generalización del método univariado de Denton
(1971) al caso multivariado.
B. Método de Di–Fonzo (1990)
Di–Fonzo (1990) supone que se cuenta con H series agregadas Yh ,
h = 1, ... , H, cada una de dimensión S  1. El problema consiste en estimar
los vectores correspondientes de alta frecuencia yh , h = 1, ... , H, de dimensión
N
1. El problema consiste en estimar
los vectores correspondientes de alta frecuencia yh , h = 1, ... , H, de dimensión
N  1, con N = M S, donde M son los subperiodos de cada periodo. Al
igual que algunos métodos univariados, se supone que existe una relación
lineal entre las variables desagregadas y un conjunto de variables indicadoras:
1, con N = M S, donde M son los subperiodos de cada periodo. Al
igual que algunos métodos univariados, se supone que existe una relación
lineal entre las variables desagregadas y un conjunto de variables indicadoras:
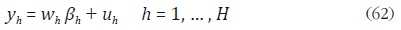
donde wh es una matriz de dimensión N  ph que contiene las variables indicadoras
asociadas a la serie h, βh es un vector de dimensión ph
ph que contiene las variables indicadoras
asociadas a la serie h, βh es un vector de dimensión ph  1 de coeficientes
desconocidos y uh es un vector aleatorio con media cero y E(uk uh')
= Vkh , con k, h = 1, ... , H. Como caso particular, cuando H = 1 la solución
al problema de desagregación se obtiene a partir de las metodologías univariadas
descritas en la sección anterior.
1 de coeficientes
desconocidos y uh es un vector aleatorio con media cero y E(uk uh')
= Vkh , con k, h = 1, ... , H. Como caso particular, cuando H = 1 la solución
al problema de desagregación se obtiene a partir de las metodologías univariadas
descritas en la sección anterior.
El sistema de ecuaciones descrito en (62) puede escribirse como:
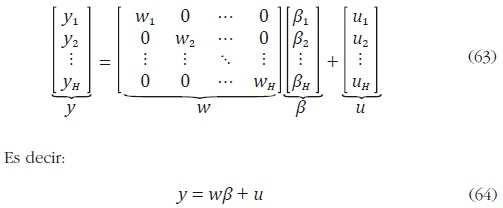
donde y es el vector de valores de alta frecuencia no observados de dimensión
NH  1, w es una matriz diagonal en bloques de variables indicadoras
observadas en alta frecuencia de dimensión NH
1, w es una matriz diagonal en bloques de variables indicadoras
observadas en alta frecuencia de dimensión NH  p, con
p, con 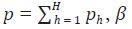 es
un vector de parámetros de dimensión p
es
un vector de parámetros de dimensión p  1, y u es un vector aleatorio de dimensión
NH
1, y u es un vector aleatorio de dimensión
NH  1 con media cero y matriz de covarianzas V, donde el bloque
kh de V está dado por Vkh, k, h = 1, ... , H.
1 con media cero y matriz de covarianzas V, donde el bloque
kh de V está dado por Vkh, k, h = 1, ... , H.
Di Fonzo define la restricción de agregación contemporánea como:

De forma similar, esta restricción se puede escribir como:

con jH un vector de unos de dimensión H  1.
1.
Por otro lado, el conjunto de restricciones de agregación temporal está
dado por 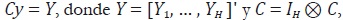 donde C es la matriz
de agregación temporal dada en (4). De esta forma, el conjunto completo de
restricciones de agregación, temporal y contemporánea, está dado por:
donde C es la matriz
de agregación temporal dada en (4). De esta forma, el conjunto completo de
restricciones de agregación, temporal y contemporánea, está dado por:

En la expresión anterior 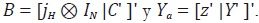 Premultiplicando
(63) por la matriz B, se tiene:
Premultiplicando
(63) por la matriz B, se tiene:
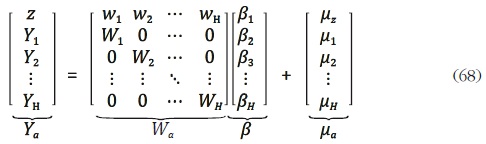
donde Wh = Cwh son matrices de variables indicadoras agregadas temporalmente
de dimensión S  ph, y µh = Cuh son vectores de innovaciones de
dimensión S
ph, y µh = Cuh son vectores de innovaciones de
dimensión S  1, con h = 1, ... , H. Adicionalmente,
1, con h = 1, ... , H. Adicionalmente, 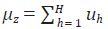 es el vector
de las innovaciones agregadas contemporáneamente. El modelo (68) puede
reescribirse como Ya = Wa β + µa , donde Wa = Bw y µa = Bu es un vector
aleatorio con matriz de covarianzas de la forma Va = BVB', la cual es singular
debido a que existe colinealidad entre la restricción contemporánea y las
temporales.
es el vector
de las innovaciones agregadas contemporáneamente. El modelo (68) puede
reescribirse como Ya = Wa β + µa , donde Wa = Bw y µa = Bu es un vector
aleatorio con matriz de covarianzas de la forma Va = BVB', la cual es singular
debido a que existe colinealidad entre la restricción contemporánea y las
temporales.
Di–Fonzo muestra que, para los problemas de distribución e interpolación, el mejor estimador lineal insesgado de y está dado por:
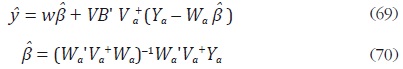
donde Va + es la inversa generalizada de Moore–Penrose de Va. Adicionalmente, la matriz de covarianzas del error es:
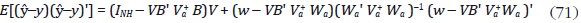
Di Fonzo supone que los errores de alta frecuencia son ruido blanco.
Adicionalmente, para simplificar el proceso de estimación se redefine la matriz B de la siguiente forma:
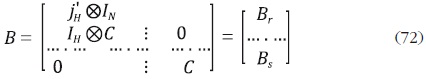
Di–Fonzo muestra que la matriz B tiene rango r = N + S(H – 1), y define
las matrices P y R de dimensión S  r y (r + S)
r y (r + S)  r, respectivamente, como:
r, respectivamente, como: 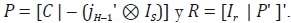 De esta forma, se tiene que BS = PBr y B = RBr . Igualmente, se puede mostrar que:
De esta forma, se tiene que BS = PBr y B = RBr . Igualmente, se puede mostrar que:
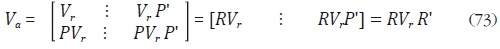
donde Vr = E(µr µr') = Br VBr' es una matriz de covarianzas r  r de rango
completo con µr = Br u.
r de rango
completo con µr = Br u.
Incorporando las definiciones anteriores, los estimadores 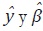 descritos
en (69) y (70) se pueden escribir como:
descritos
en (69) y (70) se pueden escribir como:
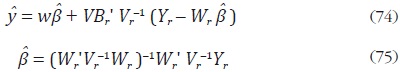
con Yr = Br Y y Wr = Br wr. Cuando los errores ut son ruido blanco se tiene que el bloque kh de V, Vkh , está dado por σkh IN para h, k = 1, ... , H. Di– Fonzo muestra que:
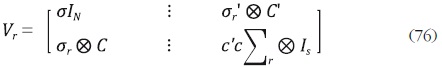
donde c está definido como en (1), 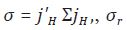 es el vector (H – 1)
es el vector (H – 1)  1 obtenido al eliminar el último elemento de
1 obtenido al eliminar el último elemento de 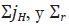 es la matriz (H – 1)
es la matriz (H – 1)  (H – 1) obtenida al eliminar la última fila y la última columna de Σ. La matriz
Σ, de dimensión H
(H – 1) obtenida al eliminar la última fila y la última columna de Σ. La matriz
Σ, de dimensión H  H está definida de tal forma que su elemento kh es σkh.
H está definida de tal forma que su elemento kh es σkh.
Por último, si Σ es desconocida, se estima como la matriz de varianzas y
covarianzas de 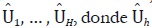 son los residuos de MCO de la regresión
del modelo en baja frecuencia Yh = Wh βh + Uh, para h = 1, ... , H.
son los residuos de MCO de la regresión
del modelo en baja frecuencia Yh = Wh βh + Uh, para h = 1, ... , H.
C. Método de Pavia y Cabrer (1999)
Pavia y Cabrer (1999) utilizan el estimador de DiFonzo (1990), pero extienden el modelo al caso en que los errores de alta frecuencia, ut , siguen un proceso autoregresivo de orden 1. De esta forma, el proceso que sigue el error de cada serie de alta frecuencia es:

Para h = 1, ... , H, y donde uh,t es el error asociado a la serie de alta
frecuencia h, en el período t, y εh,t es un proceso homocedástico con E(εh,t εk,s) = 0 cuando 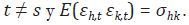 Los autores permiten, además, que
algunas de las series sigan una caminata aleatoria, es decir, Φh = 1. Suponiendo
uh,0 = 0, para todo h = 1, ... , H, el proceso (77) se puede escribir en
notación matricial para la serie h como:
Los autores permiten, además, que
algunas de las series sigan una caminata aleatoria, es decir, Φh = 1. Suponiendo
uh,0 = 0, para todo h = 1, ... , H, el proceso (77) se puede escribir en
notación matricial para la serie h como:
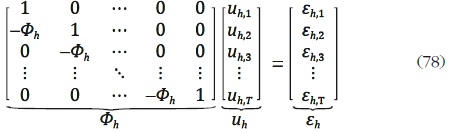
A partir de (78) se deduce que 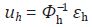 y, por lo tanto, el bloque hk de
la matriz V es
y, por lo tanto, el bloque hk de
la matriz V es 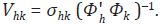 Cuando se obtiene la estimación de V, se
puede aplicar la fórmula del estimador de DiFonzo para encontrar las series
de alta frecuencia. Dado que este método exige la estimación de parámetros
adicionales sobre los errores no observados de alta frecuencia, los autores
proponen seguir el siguiente algoritmo iterativo para el caso de la distribución
de series trimestrales:
Cuando se obtiene la estimación de V, se
puede aplicar la fórmula del estimador de DiFonzo para encontrar las series
de alta frecuencia. Dado que este método exige la estimación de parámetros
adicionales sobre los errores no observados de alta frecuencia, los autores
proponen seguir el siguiente algoritmo iterativo para el caso de la distribución
de series trimestrales:
• Para cada serie h se toma el modelo de alta frecuencia no observado, que supone un proceso AR(1) en los errores, y se agrega para obtener el modelo de baja frecuencia correspondiente.
• Se estiman los coeficientes asociados a los indicadores mediante el método OLS y se obtiene los residuos de baja frecuencia.
• Se estima el parámetro autorregresivo de primer orden a partir de la serie de residuos de baja frecuencia.
• Se aproxima el parámetro autorregresivo de los errores de alta frecuencia utilizando la siguiente relación:
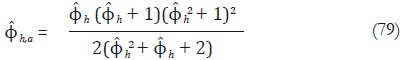
donde  es el parámetro autorregresivo estimado de los residuos de baja
frecuencia, y
es el parámetro autorregresivo estimado de los residuos de baja
frecuencia, y 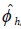 es el coeficiente de los errores de alta frecuencia a aproximar.
es el coeficiente de los errores de alta frecuencia a aproximar.
• A partir de las aproximaciones hechas en el paso anterior se construye una primera estimación de Vhh y se utiliza la ecuación del caso univariado para estimar yh.
• Con la estimación del paso anterior se estiman los residuos OLS del modelo de alta frecuencia, 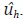
• Se obtiene un nuevo estimador de 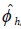 a partir de residuos anteriores. Posteriormente,
se realiza un proceso iterativo hasta alcanzar convergencia
en cada serie.
a partir de residuos anteriores. Posteriormente,
se realiza un proceso iterativo hasta alcanzar convergencia
en cada serie.
• Se efectúa la prueba de Dickey–Fuller sobre los residuos de alta frecuencia
para verificar si este proceso tiene raíz unitaria y, si este es el caso, se
reemplaza  por 1.
por 1.
• Se genera un estimador de las innovaciones del proceso AR(1) sobre los
errores de alta frecuencia, 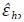 , de la siguiente manera:
, de la siguiente manera:

y se estiman las correlaciones contemporáneas entre los errores de alta frecuencia como sigue:
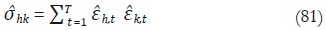
• Por último, con las estimaciones finales de σkh y 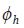 se construye V y se
aplica la fórmula del estimador multivariado de DiFonzo, de modo que se
satisfacen las restricciones de agregación temporales y contemporáneas.
se construye V y se
aplica la fórmula del estimador multivariado de DiFonzo, de modo que se
satisfacen las restricciones de agregación temporales y contemporáneas.
Una formulación similar del problema de desagregación se encuentra en
Pavia (2000). En este documento se tiene en cuenta el caso en el que la estimación
inicial del coeficiente autoregresivo de baja frecuencia del tercer paso
del algoritmo, 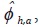 , sea menor que cero. Si esto sucede, la fórmula del paso
cuarto puede generar más de una solución. En este caso, el autor propone
utilizar la aproximación propuesta por Cavero et al. (1994) para la estimación
inicial de la serie de alta frecuencia.
, sea menor que cero. Si esto sucede, la fórmula del paso
cuarto puede generar más de una solución. En este caso, el autor propone
utilizar la aproximación propuesta por Cavero et al. (1994) para la estimación
inicial de la serie de alta frecuencia.
En Pavia y Cabrer (2008) se presenta una aplicación del método propuesto por ellos en 1999, e introducen una restricción adicional que tiene en cuenta una agregación de tipo regional; ésta restricción consiste en la agregación a nivel nacional de datos observados en diferentes regiones.
Aunque el método de Pavia y Cabrer es una extensión del método de DiFonzo, implica la mezcla de variables integradas de orden uno y de orden cero. Sin embargo, los autores no presentan una teoría estadística apropiada para realizar estimaciones con esta combinación de órdenes de integración.
D. Método Propuesto
En esta sección se propone una extensión del método de Di–Fonzo (1990) diferente a la realizada por Pavia y Cabrer (1999) y sus extensiones. Como se comentó anteriormente, el método de Di–Fonzo asume que los errores de alta frecuencia de la ecuación (64) son ruido blanco. En analogía a las metodologías de desagregación univariadas, un supuesto menos exigente corresponde a un modelo autorregresivo de orden uno sobre estos errores. En este contexto se puede asumir que estos errores siguen un modelo VAR(1) definido de la siguiente forma:
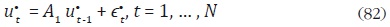
donde el superíndice 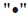 indica que los componentes de los vectores corresponden
a diferentes variables en el mismo periodo de tiempo. En el caso de
un VAR diagonal, la expresión (82) se puede reescribir como:
indica que los componentes de los vectores corresponden
a diferentes variables en el mismo periodo de tiempo. En el caso de
un VAR diagonal, la expresión (82) se puede reescribir como:
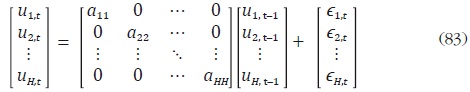
Los errores de la ecuación (82), 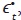 , siguen un proceso ruido blanco multivariado
con matriz de varianzas y covarianzas, Γ0 , de dimensión H
, siguen un proceso ruido blanco multivariado
con matriz de varianzas y covarianzas, Γ0 , de dimensión H  H. Por
otro lado, –1 < ahh< 1 para h = 1, ... , H, lo que implica un proceso estacionario.
H. Por
otro lado, –1 < ahh< 1 para h = 1, ... , H, lo que implica un proceso estacionario.
Dado que los errores de la ecuación (64) siguen un VAR(1) diagonal, su matriz de covarianzas V es:8
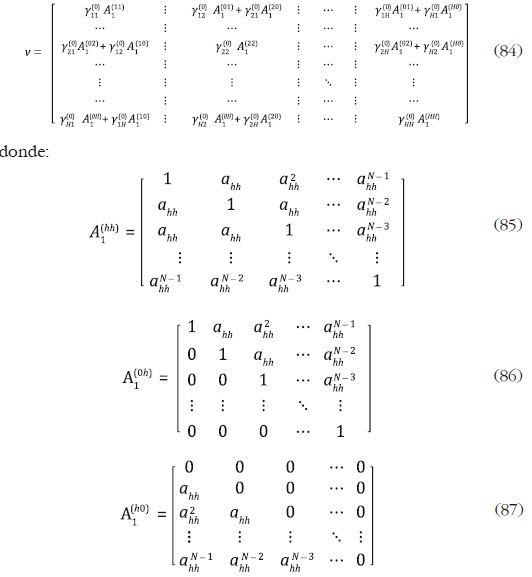
para h = 1, ... , H. Por su parte, para un modelo VAR (1) diagonal la matriz Γ0 tiene la forma:
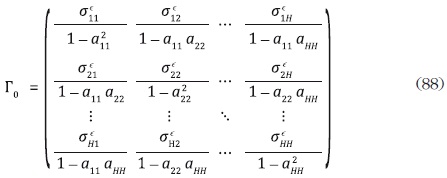
donde 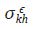 es el elemento kh de la matriz de varianzas y covarianzas contemporáneas
de
es el elemento kh de la matriz de varianzas y covarianzas contemporáneas
de 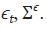 De esta forma, la matriz V únicamente depende de los
parámetros
De esta forma, la matriz V únicamente depende de los
parámetros 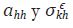 para k, h = 1, ... , H.
para k, h = 1, ... , H.
En resumen, el objetivo de la desagregación es obtener 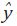 utilizando las
ecuaciones (69) y (70). Estas dependen de los datos observados y de la matriz
V. Si se supone que los errores de la ecuación (64) siguen un modelo VAR
(1) diagonal, la matriz V dependerá a su vez de las matrices A1 y Σε y, por
consiguiente, de los parámetros
utilizando las
ecuaciones (69) y (70). Estas dependen de los datos observados y de la matriz
V. Si se supone que los errores de la ecuación (64) siguen un modelo VAR
(1) diagonal, la matriz V dependerá a su vez de las matrices A1 y Σε y, por
consiguiente, de los parámetros 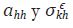 para k, h = 1, ... , H. Esto implica
que para obtener una estimación de las series desagregadas, bajo un VAR (1),
se debe contar con una estimación de los parámetros de las matrices A1 y Σε.
para k, h = 1, ... , H. Esto implica
que para obtener una estimación de las series desagregadas, bajo un VAR (1),
se debe contar con una estimación de los parámetros de las matrices A1 y Σε.
En el caso univariado Chow y Lin (1971) realizan varias propuestas para resolver este problema. A continuación se realiza una extensión de una de estas propuestas para el caso multivariado, con la cual se pueden obtener estimaciones de los parámetros a11, ... , aHH .
El método propuesto utiliza un algoritmo iterativo que parte de la ecuación (64) en forma agregada:
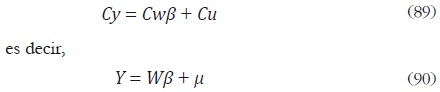
La ecuación (90) se puede reescribir en términos de bloques para cada variable h, h = 1, ... , H como sigue:
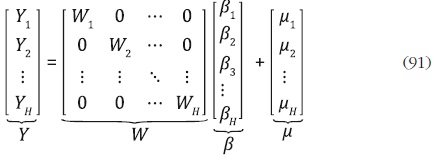
Como primer paso, se estima a través de OLS el modelo (91) para el
bloque que corresponde a la variable h para h = 1, ... , H, es decir Yh = Wh
βh + µh . Este método de estimación supone que 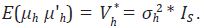 Posteriormente, se generan los residuos
Posteriormente, se generan los residuos 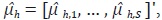 y se calcula la
correlación de primer orden,
y se calcula la
correlación de primer orden, 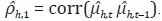
Teniendo en cuenta el supuesto sobre los errores de alta frecuencia, μh = Cuh , la estimación de la correlación de primer orden de μh corresponde al elemento de la primera fila y segunda columna de la matriz E(μh μh') = CVhh C ', donde Vhh es el bloque hh de la matriz V. De esta forma, para el caso de distribución de series trimestrales a mensuales, se tiene la siguiente relación:
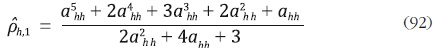
Por lo tanto,
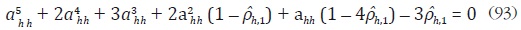
Un estimador de ahh , para h = 1, ... , H, se puede encontrar resolviendo para ahh la ecuación (93).9
Por otro lado, para el caso de distribución de series trimestrales a mensuales, los elementos de la matriz Σε se pueden estimar de la siguiente forma:
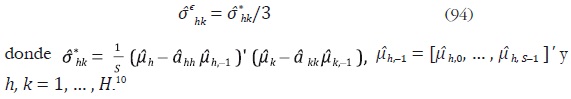
Una vez estimados los coeficientes de las matrices A1 y Σε se obtienen
estimaciones iniciales del vector de parámetros asociados a las series indicadoras, 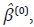 , y del vector de series desagregadas,
, y del vector de series desagregadas, 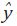 (0), utilizando las ecuaciones
(70) y (69), respectivamente.
(0), utilizando las ecuaciones
(70) y (69), respectivamente.
Como segundo paso, se generan unos nuevos residuos del modelo (90) a partir de la estimación inicial del vector de parámetros asociado a las series indicadoras:
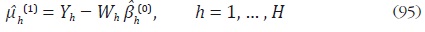
Al igual que la etapa anterior se estiman los coeficientes del vector 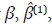 y el vector de series desagregadas,
y el vector de series desagregadas, 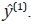
Posteriormente, se repite el paso anterior R veces, hasta obtener convergencia
en el vector 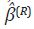 y en el vector de series desagregadas,
y en el vector de series desagregadas, 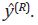
E. Método de Moauro y Savio (2005)
Estos autores proponen una metodología basada en modelos de series de
tiempo aparentemente no relacionadas o SUTSE, para lo cual utilizan un modelo
de tendencia lineal local multivariado sobre un vector de series de tiempo 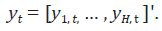 Este modelo es especificado de la siguiente forma:
Este modelo es especificado de la siguiente forma:
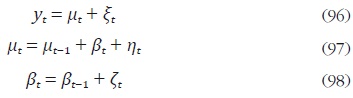
donde βt es la pendiente estocástica, 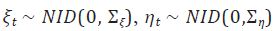 y
y
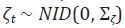 son vectores aleatorios de dimensión H
son vectores aleatorios de dimensión H  1 no correlacionados
entre sí con matriz de varianzas y covarianzas
1 no correlacionados
entre sí con matriz de varianzas y covarianzas 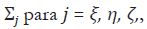 respectivamente.
El modelo puede escribirse en forma estado–espacio como sigue:
respectivamente.
El modelo puede escribirse en forma estado–espacio como sigue:

donde el vector de estado está definido como: αt = [µt', βt' ]', α1 ∼ NID(0,P), y se tiene que εt ∼ NID(0, IH). Las matrices del sistema están definidas como:
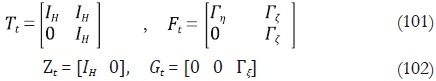
donde las matrices Γj son triangulares inferiores, tales que 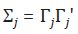 para
para
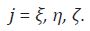
Para el caso de interpolación en el marco de desagregación temporal, el modelo definido en (99)–(100) es válido; sin embargo, para el caso de distribución se deben realizar algunas modificaciones.
Para plantear el problema de agregación se define δ como la frecuencia de
la serie desagregada (yi,t), y Si + como la frecuencia de la serie agregada (Yi,t).
Las frecuencias deben satisfacer que el cociente 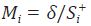 sea un número
entero para i = 1, ... , H.11 De esta forma, la serie agregada está dada por:
sea un número
entero para i = 1, ... , H.11 De esta forma, la serie agregada está dada por:
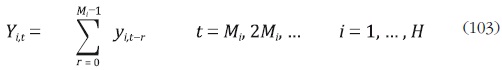
El proceso generador de las series Yt está dado por las ecuaciones (96) a (98), sin embargo, algunos de sus componentes se observan de forma agregada temporalmente, lo que implica que el vector yt contiene series observadas en alta y en baja frecuencia. En este caso el acumulador de la serie yi,t se define como:
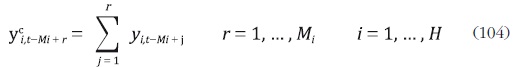
lo que implica que 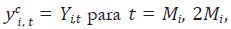 ... . En forma matricial, el
acumulador se puede escribir como:
... . En forma matricial, el
acumulador se puede escribir como:
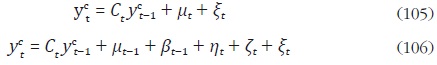
donde Ct es una matriz diagonal. Los elementos de la diagonal de esta matriz están dados por el vector [c1,t, ... , cH,t ]' y cumplen la siguiente condición para i = 1, ... , H:
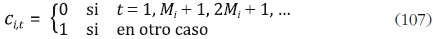
Para incluir a yi,t en el modelo definido en (99)–(100), se deben redefinir las matrices del modelo de estado espacio de la siguiente forma:
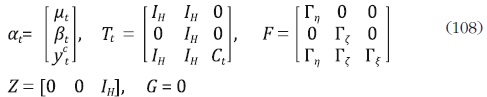
con  Finalmente, la estimación de la serie desagregada se obtiene por
máxima verosimilitud utilizando el filtro de Kalman.
Finalmente, la estimación de la serie desagregada se obtiene por
máxima verosimilitud utilizando el filtro de Kalman.
Como lo señalan los autores, una de las ventajas del modelo propuesto es que no impone una estructura a priori en los datos, ya que la especificación del modelo tiene en cuenta las características estocásticas de las series. Adicionalmente, las metodologías de Chow y Lin (1971), Fernández (1981) y Litterman (1983) se pueden expresar en términos de los modelos SUTSE.
Por otro lado, una de las desventajas de este método es que requiere especificar los valores iniciales del vector de estado y de la matriz de error cuadrático medio asociada.
IV. Ilustración empírica
En esta sección se aplica el método multivariado de Di–Fonzo (1990) y la extensión propuesta en este documento a las cuentas nacionales colombianas. La aplicación consiste en estimar las series mensuales asociadas al Producto Interno Bruto (PIB), consumo de los hogares, consumo del gobierno y formación bruta de capital a partir de las series trimestrales correspondientes, así como cinco series mensuales, cuatro variables indicadoras y las exportaciones netas. Debido a que las series a desagregar se definen como variables flujo, el problema planteado en esta sección corresponde a un problema de distribución.
Las series indicadoras (mensuales) son el índice de Producción Real de la industria manufacturera colombiana sin trilla de café (IPR), el índice del comercio minorista sin combustibles ni vehículos, los pagos totales efectuados por el gobierno sin inversión, y las importaciones de bienes de capital. Estas cuatro variables están asociadas al PIB, al consumo de los hogares, al consumo del gobierno y a la formación bruta de capital, respectivamente.
Para aplicar los métodos de desagregación temporal multivariados descritos en la sección anterior, se debe contar con una restricción contemporánea. Para ello, se debe tener en cuenta que en una economía abierta con gobierno existe la siguiente relación:
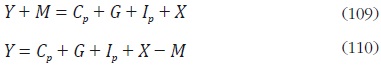
La ecuación (109) dice que la suma del producto total de la economía (Y) y las importaciones (M), se destina al consumo privado (Cp ), al gasto del gobierno (G), a la inversión privada (Ip ) y a las exportaciones (X). Además, teniendo en cuenta que el gasto del gobierno se puede desagregar en gasto público de inversión (Ig) y gasto público de consumo (Cg), se tiene que G = Cg + Ig . Si se define la inversión total (I) como la suma de la inversión pública más la inversión privada, y las exportaciones netas (XN) como las exportaciones menos las importaciones, entonces la ecuación (110) se puede escribir como:
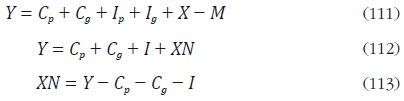
De esta forma, en términos reales para las cuentas nacionales se debe cumplir que el PIB menos el consumo de los hogares, menos el consumo del gobierno, menos la formación bruta de capital sea igual a las exportaciones netas para todos los periodos del tiempo. Por lo tanto, el agregado contemporáneo de esta aplicación es la serie de exportaciones netas reales en frecuencia mensual, que corresponde a la variable z definida en (65).
La muestra trimestral incluye el periodo comprendido entre el primer trimestre de 1994 y el primer trimestre de 2009. Por otro lado, la muestra mensual contiene información desde enero de 1994 hasta marzo de 2009. Los datos trimestrales estaban disponibles de forma desestacionalizada mientras que los datos mensuales fueron ajustados estacionalmente utilizando el procedimiento X12. Adicionalmente, todas las series se tomaron en precios constantes del año 2000.12
Los resultados muestran que las series estimadas de alta frecuencia siguen la misma tendencia que sus contrapartes de baja frecuencia, pero con mayor volatilidad. Para disminuir la volatilidad, se aplicó el filtro de Hodrick–Prescott a las series indicadoras. Los resultados de las series suavizadas muestran una menor volatilidad, pero siguen la misma tendencia que las series no suavizadas. El Gráfico 1 muestra las series estimadas de alta frecuencia para el PIB, el consumo de los hogares, la inversión y el consumo del gobierno. Es de notar que la metodología utilizada supone que los errores de alta frecuencia siguen un proceso VAR (1).
Si se supone que los errores de alta frecuencia siguen un proceso ruido blanco multivariado, se obtienen estimaciones de las series desagregadas que presentan una mayor volatilidad que bajo el supuesto de VAR (1). Por ejemplo, en el Gráfico 2 se comparan las series de alta frecuencia estimadas para el PIB con cada uno de los supuestos sobre el proceso del error, y se observa claramente una mayor volatilidad en la serie estimada suponiendo ruido blanco. Cabe anotar que este resultado también se obtiene si no se realiza el suavizamiento de las variables indicadoras por medio del filtro de Hodrick y Prescott.
Comentarios Finales
Los resultados de este documento resaltan la importancia de estudiar las características de las series a desagregar, con el objeto de aplicar el método más apropiado. Cada uno de estos métodos implica supuestos diferentes sobre las series de baja frecuencia e indicadoras. Por esto es importante tener en cuenta características estocásticas de las series, tales como el orden de integración y posibles relaciones de cointegración.
Adicionalmente, es recomendable utilizar metodologías multivariadas y no univariadas, puesto que las primeras permiten modelar dinámicas más generales. Por otro lado, las metodologías multivariadas pueden tener en consideración restricciones contemporáneas sobre las series.
En este documento se propone una nueva extensión de la metodología de desagregación multivariada de Di–Fonzo (1990); ésta supone que los errores de las series de alta frecuencia siguen un modelo VAR(1) en lugar de un proceso ruido blanco. Finalmente, la metodología propuesta es aplicada a las cuentas nacionales colombianas trimestrales con el objeto de generar estimaciones de los datos mensuales.
Como una línea de investigación futura sería relevante analizar y proponer una metodología de desagregación multivariada que sea apropiada cuando las series se encuentren cointegradas. Estos casos son de gran importancia dentro de la literatura económica.
NOTAS
1 Estas se pueden entender como variables proxy de alta frecuencia de la serie a desagregar.
2 En general N=M S, pero en el caso de extrapolación N>M S.
3 Esta matriz de ceros implica que no hay restricciones de agregación en el
periodo a extrapolar.
4 Para más detalles véase Di–Fonzo (1987).
5 El operador vec(·) convierte una matriz en un vector columna al tomar las columnas de la matriz y ponerlas una debajo de la otra.
6 De forma similar, 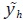 puede ser obtenido a través de cualquier método univariado expuesto
en la Sección II.
puede ser obtenido a través de cualquier método univariado expuesto
en la Sección II.
7 Estos regresores son estocásticos debido a la definición de w en (61).
8 Este resultado se muestra en el Anexo A de una versión previa del actual documento (Hurtado y Melo, 2010).
9 Chow y Lin (1971) muestran que la solución factible de este polinomio es única.
10 El resultado de la ecuación (94) se obtiene debido a que E(µh – ahh µh, –1)' (µk – akk µ) = CE(uh – ahh uh, –1)' (uk – akk uk, – 1) C'. Por lo tanto, σ*hk I = σ εhk CC '. Finalmente, para el ejercicio de distribución de series trimestrales a mensuales se tiene que CC' = 3 I.
11 Por ejemplo, para i = 1 si la frecuencia de la serie desagregada es mensual, δ = 12 y la frecuencia de la serie agregada es trimestral, S1+ = 4, entonces el cociente de frecuencias es M1 = 12/4 = 3.
12 Debido a diferencias metodológicas la serie de exportaciones netas en frecuencia trimestral no es exactamente igual a la serie agregada mensual. Por lo tanto, se ajustó la serie de exportaciones netas en frecuencia mensual con el fin de que su agregación coincidiera con la serie en frecuencia trimestral. El ajuste se realizó utilizando el método de Chow y Lin (1971).
REFERENCIAS
Barcellan, Roberto (2002). ''ECOTRIM: a program for temporal disaggregation of time series''. In: Barcellan, Roberto y Mazzi, Luigi (Eds.), Workshop on Quarterly National Accounts (pp. 79–95). Luxembourg: Eurostat.
Cavero, Jesús; Fernández–Abascal, Hermenegildo; Gómez, Isabel; Lorenzo, Carlota; Rodríguez, Beatriz; Rojo, José Luis y José Antonio Sanz (1994). ''Hacia un modelo trimestral de predicción de la economía Castellano–Leonesa. El modelo hispalink CyL'', Cuadernos Aragoneses de Economía, Vol. 4, No. 2, pp. 317–343.
Chow, Gregory y Lin An–L (1971). ''Best linear unbiased interpolation, distribution, and extrapolation of time series by related series'', Review of Economics and Statistics, Vol. 53, Issue 4, pp. 372–375.
Denton, Frank (1971). ''Adjustment of monthly or quarterly series to annual totals: An approach based on quadratic minimization'', Journal of the American Statistical Association, Vol. 66, Issue 333, pp. 99–102.
Di–Fonzo, Tommaso (1987). La stima indiretta di serie economiche trimestrali. Padova: CLEUP.
Di–Fonzo, Tommaso (1990). ''The estimation of M disaggregate time series when contemporaneous and temporal aggregates are known'', The Review of Economics and Statistics, Vol. 72, Issue 1, pp. 178–182.
Di–Fonzo, Tommaso (2002). ''Temporal disaggregation of a system of time series when the aggregate is known: optimal vs. adjustment methods''. In: Barcellan, Roberto y Mazzi, Luigi (Eds.), Workshop on Quarterly National Accounts (pp. 63–77). Luxembourg: Eurostat.
Fernández, Roque (1981). ''A methodological note on the estimation of time series'', The Review of Economics and Statistics, Vol. 63, Issue 3, pp. 471–476.
Guerrero, Víctor (1990). ''Temporal disaggregation of time series: an ARIMA– based approach'', International Statistical Review, Vol. 58, pp. 111–120.
Hurtado, Jorge Luis y Melo, Luis Fernando (2010). ''Una metodología multivariada de desagregación temporal'', Borradores de Economía 586. Banco de la República.
Litterman, Robert (1983). ''A random walk, Markov model for the distribution of time series'', Journal of Business and Economic Statistics, Vol. 1, Issue 2, pp. 169–173.
Lupi, Claudio y PARIGI, Giuseppe (2002). ''Temporal Disaggregation of Economic Time Series: Some Econometric Issues''. In: Barcellan, Roberto y Mazzi, Luigi (Eds.), Workshop on Quarterly National Accounts (pp. 111– 140). Luxembourg: Eurostat.
Moauro, Filippo y Savio Giovanni (2005). ''Temporal disaggregation using multivariate structural time series models'', Econometrics Journal, Vol. 8, Issue 2, pp. 214–234.
Pavia, José Manuel (2000). ''Desagregación Conjunta de Series Anuales: Perturbaciones AR(1) Multivariante'', Investigaciones Económicas, Vol. 24, Issue 3, pp. 727–737.
Pavia, José Manuel y Cabrer, Bernardi (1999). ''Estimating J(>1) Quarterly Time Series in Fulfilling Annual and Quarterly Constraints'', International Advances in Economic Research, Vol. 5, Issue 3, pp. 339–349.
Pavia, José Manuel y Cabrer, Bernardi (2008). ''On Distributing Quarterly National Growth among Regions'', Environment and Planning A, Vol. 40, Issue 10, pp. 2453–2468.
Rossi, Nicola (1982). ''A note on the estimation of disaggregate time series when the aggregate is known'', The Review of Economics and Statistics, Vol. 64, Issue 4, pp. 695–696.
Santos–Silva, J., y F. Cardoso (2001). ''The Chow–Lin method using dynamic models'', Economic Modelling, Vol. 18, Issue 2, pp. 269–280.