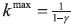 . The per–period payoff ut is given by
. The per–period payoff ut is given by ARTÍCULOS
Beneficial and harmful addictions: two sides of the same coin
Adicciones beneficiosas y adicciones perjudiciales: dos caras de la misma moneda
Des addictions bénéfiques et des addictions néfastes: les deux faces de la même médaille
Rafael López*
* Professor, Universidad Complutense de Madrid. Adress: Departamento de Fundamentos del Análisis Económico I, Campus de Somosaguas, 28223 Pozuelo de Alarcón, Madrid, España. Email: ralopez@ccee.ucm.es
–Introduction. –I. The model. –II. Beneficial Addictions under Time Consistency. –III. Beneficial Addictions under Time Inconsistency. –Concluding remarks. –References.
Primera versión recibida el 12 de mayo de 2015; versión final aceptada el 14 de septiembre de 2015
ABSTRACT
In this paper we obtain an isomorphism between harmful and beneficial addictions in a discrete–time binary choice context. The equivalence thus established allows us to study both phenomena (harmful and beneficial addictions) as two sides of the same coin. Besides the theoretical insight it provides, this dualism is also particularly useful because it readily allows for the translation of the results obtained in the domain of harmful addictions to the domain of beneficial addictions. Once the dualism is established, we analyze addictions under both timeconsistent and time–inconsistent preferences.
Key words: addiction, self–control, negative internalities, habit formation, hyperbolic discounting, naïveté, sophistication, time inconsistency
JEL classification: A12, C79, D11, D60, D91
RESUMEN
En este artículo obtenemos un isomorfismo entre las adicciones beneficiosas y las perjudiciales en un contexto de elección binaria en tiempo discreto. La equivalencia obtenida de este modo nos permite estudiar los dos fenómenos (los dos tipos de adicciones) como dos caras de la misma moneda. Además de la visión teórica que proporciona, esta dualidad también resulta particularmente útil porque permite trasladar fácilmente los resultados obtenidos en el campo de las adicciones perjudiciales al campo de las adicciones beneficiosas. Una vez establecido el dualismo, analizamos las adicciones bajo dos tipos de preferencias intertemporales: aquellas que son consistentes y aquellas que no lo son.
Palabras clave: adicción, autocontrol, internalidades negativas, formación de hábitos, descuento hiperbólico, ingenuidad, sofisticación, inconsistencia temporal
Clasificación JEL: A12, C79, D11, D60, D91
RÉSUMÉ
Dans cet article, on obtient un isomorphisme entre les addictions bénéfiques et les addictions néfastes dans un modèle avec choix binaire en temps discret. Nous obtenons une équivalence qui permet d'étudier les deux phénomènes (les deux types d'additions) comme deux faces d'une même médaille. Cette dualité est particulièrement utile car elle permet de traduire facilement les résultats obtenus dans le domaine des addictions néfastes, en résultats associés au domaine des addictions bénéfiques. Une fois le dualisme a été établi, nous analysons les additions dans le cadre des préférences intertemporelles conformes et non conformes.
Mots–clés: additions, autocontrol, internalités négatives, formation des habitudes, escompte hyperbolique, ingéniosité, sophistication, incohérence temporelle
Classification JEL : A12, C79, D11, D60, D91
INTRODUCTION
Since the seminal work by Becker and Murphy (1988), there has been a growing body of literature devoted to the study of addiction. Even though the Becker–Murphy model accounted for both harmful addictions (e.g. drug consumption) and beneficial addictions (e.g. jogging), most of the recent research has focused solely on the former (see Orphanides & Zervos, 1995; Laibson, 2001; O'Donogue & Rabin, 2002; Bernheim & Rangel, 2004; Carrillo, 2005; López, 2006; Gul & Pesendorfer, 2007). However, there is a variety of economic contexts where beneficial addictions play an important role. People might get addicted to sports, living standards, work, high levels of human capital, etc. The key feature in an addictive product is that it generates habit formation:1 past consumption of the product increases current desire for consumption. A habit–forming activity is a harmful addiction when it presents negative internalities, i.e. when it generates future costs or disutilities for the individual; whereas beneficial addictions imply positive internalities (i.e. future rewards). In general, the immediate effect of the activity could either be positive or negative in both harmful and beneficial addictions. However, the interesting cases are those where immediate and future effects go in opposite directions–when they go in the same direction, the individual behavior is trivial because there is no trade–off between present and future consequences of undertaking the activity.2 For this reason, we will assume that harmful addictions generate immediate positive pleasure and beneficial addictions generate immediate negative pleasure.
In the present paper, we establish an isomorphism between harmful and beneficial addictions that allows us to study both phenomena as two sides of the same coin: any harmful addiction can be thought of as a beneficial addiction, and vice–versa, by simply taking the negation or inverse of the addictive activity from one realm to the other.
The above dualism holds for a specific context to which we refer as a binary activity choice accumulation problem (BACAP). In a BACAP, an individual faces the binary choice of whether to undertake or not an activity in each period; and his (instantaneous) payoff depends on his current choice as well as on the history of past choices, which is captured by a state variable. To illustrate the dualism, consider the following harmful addiction example. Suppose that the activity is ''smoking one cigarette today'' and that the history of past smoking is captured by the individual's ''nicotine level''. Negative internalities are captured by assuming that smoking today produces immediate pleasure but generates future costs (because it raises the nicotine level and therefore induces detrimental health effects). Habit formation is captured by assuming that higher nicotine levels induce greater desire for current smoking. Now consider the choice problem for the same individual, where the activity is defined as ''avoiding smoking one cigarette today''. This problem presents positive internalities: by undertaking the activity, the individual renounces to the immediate pleasure (and thus incurs an immediate cost) but generates future benefits by reducing his addiction level. Moreover, this problem also has the habit–forming feature: the more the individual has avoided smoking, the lower his nicotine levels and therefore the greater the desire to keep from smoking because its associated cost is lower. Therefore, the original harmful addiction problem may be seen as a beneficial addiction one; in fact, we show that both problems are equivalent.
Besides the theoretical insight it provides, this equivalence result is appealing because of its usefulness: it allows results to be obtained for both realms of addiction by focusing just on one. For instance, previous results obtained on harmful addictions (such as in O'Donogue & Rabin, 2002; and López, 2006) can be readily translated to the domain of beneficial addictions.
Once the dualism is established, we illustrate its attractiveness by analyzing beneficial addictions under two settings: time–consistent preferences (i.e. when the intertemporal utility presents exponential discounting) and timeinconsistent preferences (i.e. intertemporal utility with hyperbolic discounting). Under the first setting, we show that an individual's behavior depends crucially on the convexity of his instantaneous utility: when convexity holds, he either always undertakes the activity or always refrains; when convexity fails, we show that there might be other absorbing states. This result is worth mentioning because previous research (on harmful addiction) has assumed convexity and yet we believe that concavity might as well be of interest. Under the second setting, the individual can either be aware (he is naïf ) or not (he is sophisticated ) of his time inconsistency. When he is aware, he engages in an intrapersonal game. We show that the isomorphism preserves the equilibria of the induced game and then we analyze the implications of naïveté vs. sophistication. In particular, we show that the implications are the same whether we have immediate costs and delayed rewards (beneficial addictions) or immediate rewards and delayed costs (harmful addictions). These contrast with the implications of naïveté vs. sophistication in a context where the activity must be performed exactly once in a finite number of periods: as O'Donoghue and Rabin (1999) show, in the doing–it–once context sophistication exacerbates misbehavior under immediate costs while it mitigates it under immediate rewards. Our analysis shows that it would be misleading to extrapolate this conclusion to a full–fledged model of intertemporal decision making, i.e. one where actions are chosen repeatedly.
The paper proceeds as follows. In Section I, we formally define a BACAP and establish the isomorphism allowing us to show that a BACAP is equivalent to its dual. In Section II, we consider addictions under time consistency and show that concavity of the utility function may yield richer patterns of behavior as opposed to the cutoff rule implied by convexity. In Section III, we consider addictions under time inconsistency and show that the isomorphism is equilibria–preserving, so that the implications of naïveté vs. sophistication are the same under both realms (beneficial and harmful) of addiction. The final section concludes.
I. The Model
We will restrict ourselves to the following class of problems:
A. Binary Activity Choice Accumulation Problem (BACAP)
In a BACAP, an individual has to choose whether to undertake (αt =1 ) or
not (αt =0 ) an activity in each period t =1,2,... The instantaneous per–period
payoff ut depends on the period's action as well as on the history of past
actions, which is assumed to be captured by a state variable k that evolves
according to k t+1 = γkt+αt with 0< γ < 1. Notice that there is a maximum value
for the state variable, 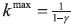 . The per–period payoff ut is given by
. The per–period payoff ut is given by
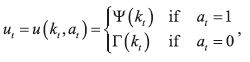
where 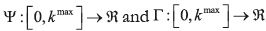 . Each period t, the individual aims
at maximizing the intertemporal utility given by
. Each period t, the individual aims
at maximizing the intertemporal utility given by
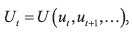
where  is the initial condition for the state variable k,
a BACAP is completely characterized by [ψ, Γ, U, γ, k1].
is the initial condition for the state variable k,
a BACAP is completely characterized by [ψ, Γ, U, γ, k1].
The main result of the following subsection is that for every BACAP B= [ψ, Γ, U, γ, k1] there is an equivalent BACAP where the activity may be viewed as the negation of the activity in B.
B. The DUAL of a BACAP
Given a BACAP B= [ψ, Γ, U, γ, k1] , define 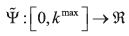 and
and

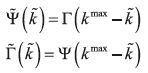
so that
 and
and 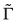 are the reflections of Γ and Ψ with respect to kmax as illustrated
in Figure 1.
are the reflections of Γ and Ψ with respect to kmax as illustrated
in Figure 1.
Now consider the problem of an individual who faces the choice of undertaking 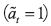 or not
or not 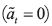 an action in each period t= 1,2,..., and where
the instantaneous payoff
an action in each period t= 1,2,..., and where
the instantaneous payoff 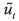 is given by
is given by
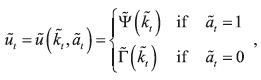
where  is assumed to evolve according to
is assumed to evolve according to
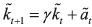 . Suppose that the individual
aims each period at maximizing the intertemporal utility
. Suppose that the individual
aims each period at maximizing the intertemporal utility
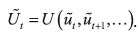
Then, for a given initial condition
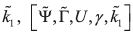 defines a BACAP.
defines a BACAP.
Definition 1. Given a BACAP B= [ψ, Γ, U, γ, k1], its DUAL is the BACAP

Definition 2. We say that a BACAP B is equivalent to a BACAP B' if
1. for any path 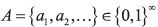 in B there is a path
in B there is a path  in B' that yields the same payoff; and
in B' that yields the same payoff; and
2. for any path  in B' there is a path
in B' there is a path 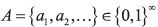 in B that yields the same payoff.
in B that yields the same payoff.
Proposition 3. A BACAP B is equivalent to its dual D(B).
Proof. Let (αt , kt) and  denote period-t actions and states in B and D(B), respectively. Consider the isomorphism
denote period-t actions and states in B and D(B), respectively. Consider the isomorphism
 that maps actions and states in B to actions and states in D(B) in the following
way:
that maps actions and states in B to actions and states in D(B) in the following
way:
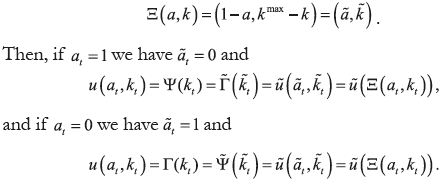
Thus, the per–period utilities associated to (αt , kt) and
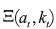 are the same.
Moreover, according to the isomorphism the evolution of kt is consistent with
the evolution of kt:
are the same.
Moreover, according to the isomorphism the evolution of kt is consistent with
the evolution of kt:

Since
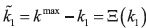 , so that the initial condition in D(B) is the image
of the initial condition of B under
, so that the initial condition in D(B) is the image
of the initial condition of B under 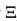 , we conclude that any path
, we conclude that any path
 in B is payoff equivalent to path
in B is payoff equivalent to path
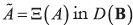 . This shows part 1 of Definition
2. To see that part 2 is also satisfied, just notice that D(D(B))= B i.e.
'' B is the dual of its dual''.
. This shows part 1 of Definition
2. To see that part 2 is also satisfied, just notice that D(D(B))= B i.e.
'' B is the dual of its dual''.
Definition 4. We say that a BACAP has Positive Internalities if Ψ and Γ are increasing in k. That is, the more the activity has been undertaken in the past, the higher the present well–being.
Definition 5. We say that a BACAP has Negative Internalities if Ψ and Γ are decreasing in . That is, the more the activity has been undertaken in the past, the lower the present well–being.
Proposition 6. If a BACAP B has Positive (Negative) Internalities, its dual D(B) has Negative (Positive) Internalities.
Proof. When Ψ and Γ are increasing (decreasing),
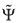 and
and
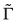 are decreasing
(increasing).
are decreasing
(increasing).
Definition 7. We say that a BACAP exhibits Habit–Formation if Ψ (k)– Γ(k) is increasing in . That is, the more the activity has been undertaken in the past (as captured by k), the higher the marginal instantaneous utility of undertaking it in the present.
Proposition 8. If a BACAP B exhibits Habit–Formation, its dual D(B) exhibits Habit–Formation.
Proof. If Ψ (k)– Γ(k) is increasing, then  is increasing.
is increasing.
Definition 9. We say that a BACAP presents Harmful Addiction if it exhibits Habit Formation and Negative Internalities. We say that a BACAP presents Beneficial Addiction if it exhibits Habit Formation and Positive Internalities.
Proposition 10. If a BACAP B presents Harmful (Beneficial) Addiction, its dual D(B) exhibits Beneficial (Harmful) Addiction.
Proof. Direct from Propositions 6 and 8.
Let
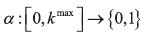 rule or strategy in a BACAP B, that is, for each
state level k, α(k) prescribes an admissible action. Define
rule or strategy in a BACAP B, that is, for each
state level k, α(k) prescribes an admissible action. Define
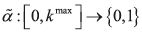 as the rule in D(B) given by
.
as the rule in D(B) given by
.
Proposition 11. If α induces path A in a BACAP B, then 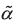 induces path
induces path  (A) in D(B).
(A) in D(B).
Proof. Suppose that at some period t, state levels are kt and
 in B and D(B) respectively. Then prescribes in B action αt = α(kt) and induces
state level
in B and D(B) respectively. Then prescribes in B action αt = α(kt) and induces
state level  ; and
; and 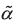 prescribes in D(B) action
prescribes in D(B) action 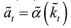 and
induces state level
and
induces state level 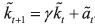 . Now notice that
. Now notice that

and
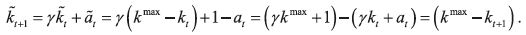
Therefore, the proposition follows by induction and the fact that 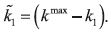 .
.
The above proposition shows that, given a strategy α in a BACAP B,
strategy
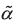 as given by expression (1) has the natural interpretation of being
the strategy in D(B) induced by applying the isomorphism
as given by expression (1) has the natural interpretation of being
the strategy in D(B) induced by applying the isomorphism 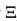 to α. Thus, with
a slight abuse of notation we will refer to it as
to α. Thus, with
a slight abuse of notation we will refer to it as 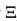 (α). Notice that, as is shown
in the proof of Proposition 3, path in B is payoff equivalent to path
(α). Notice that, as is shown
in the proof of Proposition 3, path in B is payoff equivalent to path 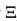 (A) in
D(B). Therefore, we readily obtain the following proposition:
(A) in
D(B). Therefore, we readily obtain the following proposition:
Proposition 12. Strategies α and 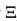 (α) are payoff equivalent.
(α) are payoff equivalent.
Proof. Let A be the path generated by strategy α in B. By definition,
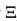 (α) is the strategy in D(B) induced by applying the isomorphism
(α) is the strategy in D(B) induced by applying the isomorphism 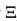 to α and
therefore the path it generates in D(B) is precisely
to α and
therefore the path it generates in D(B) is precisely 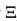 (A). The proof of Proposition 3 shows that paths A and
(A). The proof of Proposition 3 shows that paths A and 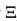 (A) are payoff equivalent. Therefore, the
strategies generating them are also payoff equivalent.
(A) are payoff equivalent. Therefore, the
strategies generating them are also payoff equivalent.
We conclude this section by giving examples that motivate the study of BACAPs presenting Addiction.
C. Some examples presenting Addiction
1. Drug consumption
Suppose that the activity is ''smoking one cigarette'' and k represents the individual's addiction level. Let ƒ (kt) be the utility associated to addiction level kt irrespective of what the individual's current choice is. Because of the detrimental effects of past smoking in current health, it is natural to assume that ƒ is decreasing in k. Further, suppose that x > 0 reflects the intrinsic pleasure of smoking one cigarette and w(kt) is the withdrawal cost, which we assume increasing in kt because the more the person has smoked in the past the harder for him to refrain from current smoking. Then, the instantaneous per–period utility is given by
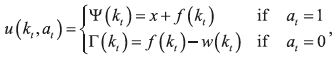
and the (harmful) addictive properties of smoking are reflected by negative internalities (Ψ and Γ decreasing) and habit formation (w increasing). This is precisely the kind of model studied by O'Donoghue and Rabin (2002).
2. Jogging
Suppose the activity is ''one hour of jogging'', so that represents the fitness level. Let g(kt) be the utility derived from having fitness level kt. This is a utility the individual enjoys at time t irrespective of what his current choice is; it includes the health benefits from past exercising and therefore is increasing in kt. Also, let e > 0 be the effort or cost associated to ''one hour of jogging'' when the individual has never exercised before (i.e.k = 0). It seems natural to assume that this cost decreases as the fitness level increases. We capture this by letting the cost be c(kt) = e –h (kt), with h (kt) increasing and h(0) = 0 .
Notice that this allows for the jogging activity to even become ''pleasurable'' (i.e. when for some k, h (k)> e), ). Then, the instantaneous per–period utility is given by
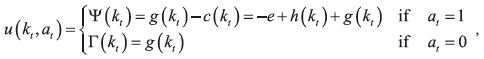
and the (beneficial) addictive properties of jogging are reflected by positive internalities (Ψ and Γ increasing) and habit formation (h increasing).
3. Conspicuous consumption
Suppose that the main source of utility for an individual is his living standard (or status), which we denote by and can only be raised by the activity of conspicuous consumption (cf. Veblen). For instance, think of this activity (α =1 ) as ''offering a Great–Gatsby–type party''. Let g(k) be the utility associated to status k that the individual enjoys irrespective of his current choice. Offering the party has an intrinsic instantaneous utility but it also produces a positive internality because it raises the host's status for next period. Further, let be the intrinsic utility of the party experienced by the host. We may assume that is increasing in k (for instance, people attending the party are kinder to the host the higher his status is). If e > 0 represents the effort or cost of offering the party, the instantaneous per–period utility is given by
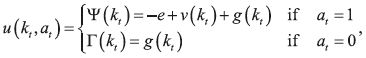
and the (beneficial) addictive properties of conspicuous consumption are reflected by positive internalities (Ψ and Γ increasing) and habit formation (ν increasing).
4. Investment in Human Capital
Suppose that the individual has a unit of free time and a unit of working time each period. The working time unit is exerted in a productive activity whose productivity g(k) depends positively on the accumulated human capital k. The individual may use his free time in either learning (α=1), which might be interpreted as investment in human capital and therefore increases his stock k, or in an alternative activity (α=0), which may be leisure or some other productive activity that does not affect k. When he decides to use his free time in the alternative activity, he obtains an instantaneous utility e > 0, which can be thought of as the pleasure derived from leisure or the profits from the alternative productive activity. If he devotes his free time to learning, he incurs a cost c(k), which is decreasing in k and may eventually become negative (i.e. the individual ''enjoys'' learning). Therefore, the instantaneous per–period utility is given by

and the (beneficial) addictive properties of investment in human capital are reflected by positive internalities (ψ and Γ increasing) and habit formation (–c increasing).
II. Beneficial Addictions under Time Consistency
Consider a BACAP B= [ψ, Γ, U, γ, k1] presenting beneficial addiction and where the functional U takes the specific form
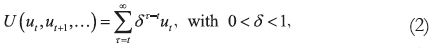
i.e. where we have time separability and exponential discounting. Let 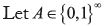 denote a behavior path, that is, an infinite sequence of admissible actions.
Keeping in mind the jogging example of the previous section, we will use
(from ''exercising'') to denote the behavior path where the individual always
undertakes the activity, that is, E = (1,1,...), and N (from ''never exercising'')
will denote the behavior path where the individual never undertakes the activity,
that is, N = (0,0,...).
denote a behavior path, that is, an infinite sequence of admissible actions.
Keeping in mind the jogging example of the previous section, we will use
(from ''exercising'') to denote the behavior path where the individual always
undertakes the activity, that is, E = (1,1,...), and N (from ''never exercising'')
will denote the behavior path where the individual never undertakes the activity,
that is, N = (0,0,...).
We will see that the optimal decision rule and long–run behavior depend crucially on the convexity of Ψ and Γ.
A. Ψ and Γ convex
From the previous section, we know that B is equivalent to its dual
 . By Proposition 6, we know that D(B) presents
harmful addiction. Notice that
. By Proposition 6, we know that D(B) presents
harmful addiction. Notice that 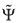 and
and 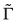 are also convex. In O'Donoghue and
Rabin (2002), it is shown that a BACAP as D(B) the optimal decision rule
of the agent is of the cut–off type. That is, there exists a critical state level
are also convex. In O'Donoghue and
Rabin (2002), it is shown that a BACAP as D(B) the optimal decision rule
of the agent is of the cut–off type. That is, there exists a critical state level
 such that the optimal action is
such that the optimal action is 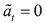 for levels below
for levels below  and
and 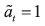 for levels
above
for levels
above 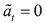 . Therefore, the optimal decision rule takes the form
. Therefore, the optimal decision rule takes the form
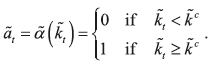
The reason for this is that the time consistency implied by the intertemporal
utility (2) allows for the use of a value function 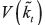 that happens to be
convex when
that happens to be
convex when  and
and 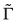 are convex. Therefore, at any time the agent chooses
are convex. Therefore, at any time the agent chooses
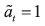 if and only if
if and only if
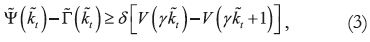
i.e. if and only if the marginal instantaneous benefits  offset the
marginal future costs
offset the
marginal future costs 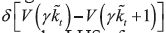 of the action. Now, because of
the habit–forming feature, the LHS of expression (3) is increasing, while the
convexity of the value function implies that the RHS of the same expression
is decreasing, and therefore we get the existence of
of the action. Now, because of
the habit–forming feature, the LHS of expression (3) is increasing, while the
convexity of the value function implies that the RHS of the same expression
is decreasing, and therefore we get the existence of  .
.
Now, because of the equivalence between B and D(B), we readily obtain
Proposition 13. In a BACAP B= [ψ, Γ, U, γ, k1] presenting beneficial addiction
with Ψ and Γ convex and intertemporal utility U given by (2), the optimal decision rule is
of the cutoff type. That is, there exists a critical state level 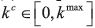 such that
such that
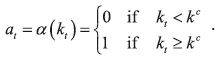
Remark 14. Notice that when Ψ and Γ are convex, long–run behavior depends totally
on the initial condition 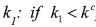 , the individual will never undertake the activity (his realized behavior path is N), while when k1≥ kc he will undertake it forever (his realized
behavior path is E). Therefore, there are only two absorbing states: 0 (when k1 < kc) and kmax (when k1 ≥ kc). This changes dramatically if we relax the convexity assumption
as the following subsection shows.
, the individual will never undertake the activity (his realized behavior path is N), while when k1≥ kc he will undertake it forever (his realized
behavior path is E). Therefore, there are only two absorbing states: 0 (when k1 < kc) and kmax (when k1 ≥ kc). This changes dramatically if we relax the convexity assumption
as the following subsection shows.
B. Ψ and Γ concave
Suppose now that and are concave. Even though we still may make use of a value function by virtue of intertemporal utility (2), this value function may not be convex nor concave. So the type of analysis used in the previous subsection is of no use. The concavity assumption makes the analysis much more complicated, but it also allows for a variety of pattern behaviors: the optimal decision rule may no longer be of the cutoff type; long–run behavior may be independent of initial conditions; and there might be other absorbing states. In particular, it is possible to observe non–monotonic behavior where the individual alternatively switches from undertaking the activity to refraining.3
C. Assuming Convexity
As we have seen, characterization of behavior is very simple under the convexity (of Ψ and Γ ) assumption while it may be a very complicated task when we relax it. Assuming convexity is appealing because of its tractability, but it may be unsatisfactory for modeling some addictions. In essence, what the convexity assumption posits is that there are increasing marginal returns in the state variable. However, we believe that there are some realms of addiction where the opposite would hold. Consider, for instance, the jogging example provided in the previous section: perhaps the most reasonable assumption is decreasing marginal returns to the fitness level (i.e. Ψ and Γ concave). The same goes for the investment in human capital example: the standard would be to assume decreasing marginal returns to the accumulated human capital. In their harmful addiction model, O'Donoghue and Rabin (2002) posit the convexity assumption arguing that ''the more addicted the person becomes, the less a given increase in k hurts his instantaneous utility, and therefore the less harm hitting does to future utility''. This is debatable:4 It could be a reasonable assumption for some drugs, say ''soft'' drugs, but it may not be too realistic for ''hard'' drugs such as heroin.
We believe that the concavity assumption deserves attention since it may be appropriate for some addiction contexts.
III. Beneficial Addictions under Time Inconsistency
Suppose now that the functional U takes the specific form5
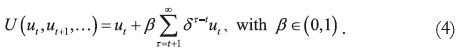
The present bias reflected in the parameter β induces the time inconsistency: because of the greater taste for immediate gratification, an optimal behavior path at some date may no longer be optimal at a further date. Therefore, an optimal behavior path may not be implementable because future selves may have incentives to deviate (here, of course, we are not allowing for commitment possibilities). When the individual is fully unaware of his timeinconsistency (i.e. he is naïf ), he chooses his action according to the behavior path that maximizes (4) believing (wrongly) that his future selves will stick to it. When the individual is fully aware of his time–inconsistency (i.e. he is sophisticated ), he engages in an intrapersonal game: he plays against his future selves by maximizing (4) subject to the intended behavior path to be followed. In the infinite horizon case, this intrapersonal game will normally present multiple Markov Perfect equilibria, which is the natural solution concept to be called upon. In what follows, it will be useful to distinguish between a desired behavior path (DBP), that is, an infinite sequence of actions solving expression (4); and a realized behavior path (RBP), that is, a path actually followed by all selves.
The implications of naïveté vs. sophistication have been studied in O'Donoghue and Rabin (2002) and in López (2006) for a BACAP presenting harmful addiction under time inconsistency as given by expression (4). We may now apply the duality established in Subsection I. B to translate their results into BACAPs with beneficial addictions. It is important to note that we will consider only the case where and are convex. We do so because those studies presented this assumption.
A. Naïf behavior
O'Donoghue and Rabin (2002) show that in a BACAP B presenting harmful addiction a naïf follows a cutoff rule , that is, there is a critical state level kn such that
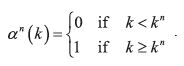
Moreover, it happens that for levels below kn the DBP is R = 00000..., while for levels above kn the DBP is either 0 = 1000...or H = 1111.... A naïf has self–control problems (or time inconsistency) whenever is the DBP: Believing that he is able to follow it, he will undertake the activity; but, by doing so, he raises his state level for next period and therefore he does not stick to 0. In fact, the RBP is either R (for any level below kn) or H (for any level above kn).
Because of the equivalence between B and D(B), (in particular because
of Propositions 11 and 12) strategy 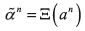 describes naïf behavior in
D(B). Therefore,
describes naïf behavior in
D(B). Therefore,

which is equivalent to:
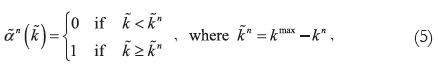
and thus the RBP of a naïf in D(B) is either
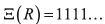 (for any level above
(for any level above
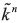 ) or
) or 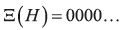 (for any level below
(for any level below 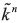 ).
).
Since any BACAP presenting beneficial addiction can be thought of as the dual of some BACAP presenting harmful addiction, naïf behavior for beneficial addictions is completely characterized by expression (5).
B. Sophisticated behavior
When there is MPE multiplicity (as it is normally the case with an infinite
horizon) in the induced intrapersonal game, sophisticated behavior would
depend on the particular equilibrium selection. Rather than characterizing
sophisticated behavior in a BACAP B6, what we want to point out is that the
isomorphism 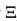 is equilibrium–preserving:
is equilibrium–preserving:
Proposition 15. If strategy constitutes a MPE of a BACAP B, then strategy 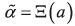 constitutes a MPE of D(B).
constitutes a MPE of D(B).
Proof. Because of Propositions 11 and 12, if there were a profitable deviation
from 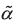 in D(B) then there would be a profitable deviation from α in
B: just apply the isomorphism
in D(B) then there would be a profitable deviation from α in
B: just apply the isomorphism 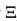 to the deviation.
to the deviation.
Therefore, the dualism also applies for sophisticated behavior: if some
strategy  describes sophisticated behavior in a BACAP B, then strategy
describes sophisticated behavior in a BACAP B, then strategy
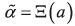 describes sophisticated behavior in D(B). We turn now to compare
sophisticated versus naïf behavior.
describes sophisticated behavior in D(B). We turn now to compare
sophisticated versus naïf behavior.
C. Naïveté vs. sophistication
We will use the following notation: For any strategy
 and any level
and any level 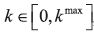 , let V (k;α) denote the value (i.e. the maximal intertemporal
utility) of following strategy with starting state level k. For any behavior path
, let V (k;α) denote the value (i.e. the maximal intertemporal
utility) of following strategy with starting state level k. For any behavior path
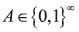 and any level
and any level 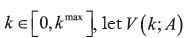 denote the value
of following path A with starting state level k.
denote the value
of following path A with starting state level k.
Suppose that strategy αs describes sophisticated behavior in a BACAP B (i.e. αs is the selected MPE of the induced game). Then, for a given initial state level k a sophisticated would be better off than a naïf if and only if

From the previous subsections, we know that in D(B) naïf and sophisticated
behaviors are described by strategies 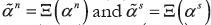 , respectively.
Proposition 12 implies that
, respectively.
Proposition 12 implies that  ,
where
,
where 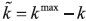 , and therefore we obtain
, and therefore we obtain
Proposition 16. If for some level a sophisticated is better off than a naïf in a
BACAP B, for level 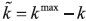 a sophisticated is better off than a naïf in D(B).
a sophisticated is better off than a naïf in D(B).
Definition 17. We say that sophistication mitigates (exacerbates) misbehavior in a BACAP B, if
1. for all state levels a sophisticated is better off (worse off) than a naïf; and
2. there are state levels for which a sophisticated is strictly better off (worse off) than a naïf.
The above proposition directly implies
Proposition 18. If sophistication mitigates (exacerbates) misbehavior in a BACAP , it mitigates (exacerbates) misbehavior in D(B).
Notice that the above proposition implies that the implications of sophistication vs. naïveté are the same for harmful and beneficial addictions since one may be seen as the dual of the other.
We conclude this section by discussing a result obtained by O'Donoghue and Rabin (2002), namely, there are BACAPs presenting harmful addiction where sophistication exacerbates misbehavior. It is important to notice that this result depends not only on the characteristics of the BACAP, but also on the particular equilibrium selection describing sophisticated behavior. Regarding the characteristics, the BACAP must satisfy a condition that they refer to as the Inevitability Condition (IC). In López (2006), it is shown that IC is equivalent to
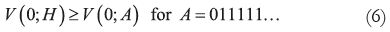
that is, for an un–addicted individual (k=0) the value of always hitting is higher than the value of refraining today and hitting from tomorrow ever after. It is also shown that expression (6) implies .

The term Inevitability Condition is due to the following interpretation of expression (7): If sophisticated individuals ''perceive that addiction is inevitable in the sense that no matter what they do today their future selves will hit forever after'', they might as well start hitting today.
Regarding the equilibrium selection, they propose the equilibrium corresponding to the limit of the unique finite–horizon MPE as the horizon becomes long–we will refer to this equilibrium as the ORE. O'Donoghue and Rabin (2002) show that when IC holds the ORE is characterized by strategy
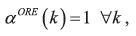
and therefore sophistication exacerbates misbehavior: A sophisticated is worse off than a naïf for all state levels, and strictly worse off for any level below (the threshold level characterizing naïf behavior).
Proposition 18 directly implies the following:
Proposition 19. There are BACAPs presenting beneficial addiction where sophistication exacerbates misbehavior.
Proof. Just consider the dual of a BACAP satisfying (7) and as the selected
equilibrium describing sophisticated behavior strategy
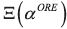 .
.
We believe that the above result is worth mentioning for at least two reasons. First, it challenges the general view that sophistication mitigates misbehavior when costs are immediate and rewards are delayed, as it is the case of beneficial addictions. O'Donoghue and Rabin (1999) show that this view is correct in a context where the activity has to be undertaken exactly once and there is a finite number of periods where the individual can do it. However, Proposition 19 shows that extrapolating it to the domain of BACAPs, where the activity may be repeated over time, is misleading.
Second, it relies on the selected equilibrium being the ORE, that is, the limit of the unique finite–horizon MPE as the horizon becomes long. In López (2006), other MPEs are provided such that, for BACAPs presenting harmful addiction and satisfying IC, sophistication mitigates misbehavior.
Concluding remarks
We have constructed an isomorphism that establishes a dualism between harmful and beneficial addictions: both phenomena are just two sides of the same coin. The dualism holds for the context of BACAPs, where an individual faces the binary choice of undertaking or not an activity in each period; and his payoff depends on his current choice as well as on the history of past behavior.
From a theoretical perspective, the dualism is appealing because it allows us to give insights for both realms of addiction by analyzing either one. We have shown that in a time consistent setting (i.e. when the intertemporal utility exhibits exponential discounting), whether the instantaneous utility function is convex or concave has very different implications: While under convexity the individual follows a cut–off rule, and therefore for a given initial state either always undertakes the activity or always refrains, assuming concavity may yield richer patterns of behavior. Since for some addiction contexts concavity might be the appropriate assumption, we believe that our results deserve attention and motivate further research.
We have also considered a time inconsistent setting, where the intertemporal utility function exhibits hyperbolic discounting, to study the implications of sophistication (i.e. when the individual is fully aware of his time inconsistent preferences) versus naïveté (i.e. when the individual is unaware of his time inconsistency). The isomorphism allows us to state that, whether sophistication hurts or benefits, the individual does not depend on whether costs are immediate and rewards delayed (beneficial addiction) or rewards are immediate and costs delayed (harmful addiction). This is worth mentioning because in a doing–it–once context, where the activity must be performed exactly once in a finite number of periods, sophistication benefits the individual in the former while it hurts him in the latter case, as has been shown by O'Donoghue and Rabin (1999). Therefore, extrapolating this result to the domain of addictions would be misleading. To illustrate this, we make use of the dualism to show that there are BACAPs presenting beneficial addiction where sophistication hurts the individual. Nevertheless, we also point out that to obtain this result, which in fact is a translation of a result obtained by O'Donoghue and Rabin (2002) for harmful addictions, the particular equilibrium selection for the sophisticated's intrapersonal game plays a crucial role. If we allow other dominating MPE, as the ones provided in López (2006), then sophistication would mitigate misbehavior under both harmful and beneficial addictions.
Finally, we would like to point out that the isomorphism holds for arbitrary instantaneous payoff functions (Ψ and Γ) and arbitrary intertemporal utility function (U); however, the specific evolution of the state variable we have assumed in a BACAP (i.e. kt+1 = γkt+αt) plays an important role in establishing it. Therefore, it would be of interest to consider whether the dualism still holds under more general conditions for the evolution of the state variable.
NOTES
1 Becker and Murphy (1988) refer to this feature as adjacent complementarities.
2 Imagine an activity that produces immediate pleasure and long–run positive effects; then, trivially, a rational individual will always undertake the activity. Similarly, an activity that implies both immediate and future negative effects will never be undertaken by a rational individual.
3 We have constructed examples for each of these cases. Because of their tedious technicalities, they have been omitted from the paper. However, they may be obtained upon request.
4 We believe that they are aware of this since they state that ''most results hold even if ψ and Γ are a little concave, and some do not rely at all on them being convex''.
5 This functional form was first introduced by Phelps and Pollack (1968). Because of its simplicity and tractability, it has been widely used to model self–control problems since the work of Laibson (1994).
6 This would imply characterization of MPE of the induced game and, as O'Donoghue and Rabin (2002) point out, this can be a very complicated task.
REFERENCES
Becker, Gary S. & Murphy, Kevin M. (1988). ''A Theory of Rational Addiction'', Journal of Political Economy, Vol. 96, No. 4, pp. 675–700.
Bernheim, Douglas & Rangel, Antonio (2004). ''Addiction and Cue–Triggered Decision Processes'', American Economic Review, Vol. 94, No. 5, pp. 1558–1590.
Carrillo, Juan (2005). ''To be consumed with moderation'', European Economic Review, Vol. 49, pp. 99 – 111.
Gruber, Jonathan & Koszegi, Botond (2001). ''Is Addiction 'Rational'? Theory and Evidence'', Quarterly Journal of Economics, Vol. 116, No. 4, pp. 1261–1303.
Gul Faruk & Pesendorfer, Wolfgang (2007). ''Harmful Addiction'', Review of Economic Studies, Vol. 74, No. 1, pp. 147–172.
Laibson, David (1994). ''Essays in Hyperbolic Discounting''. Economics, Massachusetts Institute of Technology.
Laibson, David (2001). ''A Cue–Theory of Consumption'', Quarterly Journal of Economics, Vol. 116, No. 1, pp. 81–119.
López, Rafael (2006). ''Addiction and Self–Control: an Intrapersonal Game'', Revista Desarrollo y Sociedad, No. 58, pp. 1–35.
O'Donoghue, Ted & Rabin, Matthew (1999). ''Doing It Now or Later'', American Economic Review, Vol. 89, No. 1, pp. 103–124.
O'Donoghue, Ted & Rabin, Matthew (2002). ''Addiction and Present–Biased Preferences''. Unpublished paper.
Phelps, Edmund S. & Pollak, Robert A. (1968). ''On Second–best National Saving and Game–equilibrium Growth'', Review of Economic Studies, Vol. 35, No. 2, pp. 185–199.