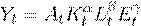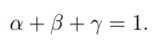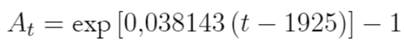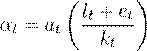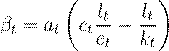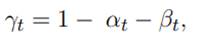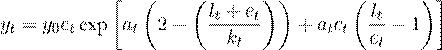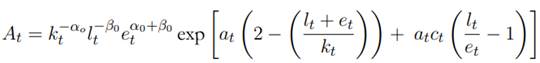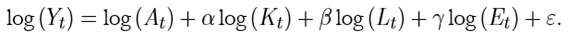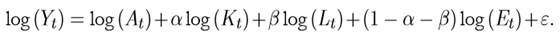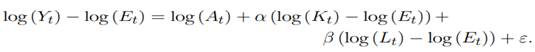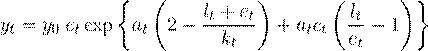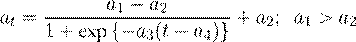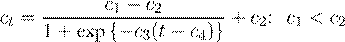Introducción
En los análisis del funcionamiento de las sociedades modernas, es de común aceptación que la energía es un factor determinante de todas las actividades económicas, productivas y sociales; de hecho, la energía puede ser considerada como el elemento clave en el proceso evolutivo y cultural del hombre (White, 1943). Después de siglos de uso de la fuerza del trabajo de los hombres y animales y del uso productivo de recursos como el agua, el viento y la madera, desde la primera fase de la Revolución Industrial se incrementó aceleradamente el uso de recursos como el carbón, el petróleo y el gas natural necesarios para crear y mover los nuevos esclavos mecánicos, construir modernas sociedades industrializadas y crear circuitos de comercio de alcance global. En dos siglos y medio, fue posible acelerar el proceso de creación de riqueza y lograr avances importantes en materia económica y social para la mayoría de las sociedades existentes.
El intenso consumo de energía aceleró la creación de riqueza (simbolizada económicamente en el PIB), consolidó el sistema capitalista y elevó al crecimiento económico al status de uno de los principales campos de análisis teórico de la economía. Dicha aceleración fue estudiada y modelada por Solow (1957) 1quien concluyó que la riqueza de los EE. UU. era explicada marginalmente por la combinación del capital (K) y el trabajo (L), y que la mayor parte de dicho crecimiento quedaría asociada al denominado residuo de Solow, el cual, para darle consistencia matemática al modelo fue explicado como un factor exógeno y tratado como una función del tiempo. Posteriormente dicho residuo se identificó con la productividad total de los factores (PTF), la tecnología en general (A), y más comúnmente con el progreso técnico. Con todo, y tal como este mismo autor reconocería después, se había formulado una teoría del crecimiento a la vez que se había dejado sin explicación el factor más importante (Solow, 1994, p. 48).
En este contexto, la teoría económica ortodoxa ha negado sistemáticamente que pueda existir una relación entre crecimiento económico y energía; en lo fundamental se argumenta que la energía es un bien intermedio que se produce y se consume en el proceso económico, cuyo peso en el producto final es marginal y es proporcional a su participación en la estructura de costos de producción. Sin embargo, desde los años setenta del siglo XX y como respuesta a la importancia que la energía lograba en la agenda de investigación económica como consecuencia de experiencia acumulada y posterior a las llamadas ‘crisis’ petroleras, el interés de los académicos e investigadores de diferentes disciplinas por establecer y formalizar dicha relación fue tomando forma y después de un largo proceso, en la literatura se reconocen dos grandes metodologías para aproximarse al análisis y las implicaciones de esta relación.
En primer lugar y desde una perspectiva ortodoxa, a partir del trabajo seminal de Kraft y Kraft (1978), se establece una relación estadística de causalidad entre el crecimiento del PIB y el consumo de energía. El camino abierto por estos autores ha sido seguido en numerosos trabajos que incluyen diversas variaciones analíticas y estadísticas, los cuales suelen ser realizados con variaciones analíticas y estadísticas para diferentes países y regiones con resultados normalmente disímiles. Entre dichos trabajos se pueden reseñar los siguientes: Akarka y Long, (1980), Yu y Choi, (1985), Nachane et al. (1988), Hwang y Gum (1991), Ebohon (1996), Cheng (1997), Asafu-Adjaye (2000), Soytas y Sari (2003), Oh y Lee (2004), Shiu y Lam (2004), Altinay y Kagarol (2004), Yoo(2006), Lee (2006), Lee y Chang (2007), Squalli (2007), Chiou et al.(2008), Chontanawat et al.(2008), Yuan et al.(2008), Belloumi (2009),Wolde Rufael (2009), Apergis y Payne (2010a, 2010b), Ozturk et al. (2010), Sharma (2010), Belke et al.(2011), Shuyun y Donghu (2011),Bildirici y Kayicky (2012), Gurgul y Lach (2012), Narayan y Popp (2012),Yalta y Cakar (2012),Yildirim y Aslan (2012), Zhang y Xu (2012), Shengfeng et al. (2012), Farhani y Ben Rejeb (2012). En el caso específico de Colombia la literatura existente registra los trabajos de Campo y Sarmiento (2011) y Barreto y Campo (2012).
La segunda metodología que se puede denominar heterodoxa, se deriva de los trabajos de autores2 que han buscado incorporar a la energía (E) como una variable adicional al capital (K) y al trabajo (L) en la función de producción estándar (Cobb-Douglas), desarrollando una metodología que sin alterar los fundamentos de la teoría neoclásica permitieran lograrlo con arreglo al mundo físico y sus leyes, de tal manera que también fuera posible calcular su aporte a la creación de riqueza, en función de la elasticidad asociada y poder medir en el tiempo su contribución al PIB. Entre los primeros intentos para lograr este propósito, cabe recordar a Berndt y Wood (1975), Allen (1979), Hannon y Joyce (1981) y Stern (1993, 2004). Con mejores resultados y buscando tender puentes para conciliar el mundo teórico de la economía con el mundo real de la física y por extensión de la biofísica, los trabajos de Kümmel (1980, 1982, 1989, 2011), Kümmel y Lindenberger (2014), Kümmel et al. (1985, 2000, 2002, 2010, 2015), Hall et al. (2001) y Lindenberger et al. (2017) han construido una metodología completa y efectiva que ha evolucionado para convertirse en una alternativa analítica que permite analizar de manera alternativa el crecimiento económico, eliminar el residuo de Solow, hacer entendible el problema de la eficiencia tanto en la producción como en el consumo y abrir debates relativos a los impactos sociales, ambientales y ahora también relativos al cambio climático3 y a la sostenibilidad de las formas de vivir y de producir de las sociedades del siglo XXI.
Dicha metodología se concreta con el denominado modelo LINEX, el cual fue inicialmente aplicado a los casos de algunos países desarrollados como EE. UU., Japón y Alemania (véase el trabajo de Hall et al., 2001). Como resultado general el nuevo factor (E) resultó tener el principal peso en la explicación de la creación de riqueza económica durante la mayor parte del siglo XX. Este logro ha sido reconocido entre otros autores por Rifkin (2011), en cuyo trabajo reconoce que por esta vía se demostró que la mayor parte de los aumentos de productividad y de crecimiento económico registrados en las sociedades industriales se debe a la energía y denominado (E) en dicho modelo.
En función de estos desarrollos metodológicos y también como resultado de sus propias investigaciones Ayres (1978, 1994, 1998, 2001), y Ayres y Warr (2003, 2005, 2009), dan un paso adicional integrando la segunda ley de la termodinámica para proponer una alternativa al tercer factor productivo denominada ahora exergía (U)4, el cual se incorpora en la función de producción Cobb-Douglas junto con los factores clásicos trabajo (L) y el capital (K). La inclusión de este tercer factor permite verificar tanto dicha relación como cuantificar el peso del aporte exergético a la creación de riqueza, esto es, en la formación del PIB. Simultáneamente y como uno de los logros más importantes de esta metodología y contenidos en su trabajo de 2009, se tiene que con la inclusión de este tercer factor se elimina el llamado residuo de Solow -lo que en otros términos implica endogenizar la tecnología- lo que resulta consistente con los resultados de los trabajos mencionados de Kümmel y demás autores asociados.
En el mismo sentido, aunque con diferentes enfoques se pueden reseñar los trabajos de Schurr et al. (1990), Stern (1993), Beaudreau (1995, 1998, 2005), Pokrovski (2003, 2007), Alam (2009), entre otros, los cuales estudian y discuten tanto la existencia e importancia de dicha relación como sus consecuencias sobre el crecimiento económico, el funcionamiento del sistema económico y sus impactos sobre el entorno natural. En efecto, la relación entre el consumo de energía, el crecimiento económico y el medio ambiente ha recibido una creciente atención en los últimos años. Los resultados presentados en trabajos como los de Esso y Keho (2016), Nahman y Antrobus (2005), Ricci (2007), y Brock y Taylor (2010), son de interés pues, aunque varían los países bajo análisis, tipo de variables asociadas a la producción y al consumo de energía y el tipo de técnicas estadísticas utilizadas para el modelamiento, muestran que en países en vía de desarrollo el nivel de contaminación aumenta hasta que los ingresos exceden un nivel umbral evidencia de la denominada curva ambiental de Kuznets (EKC).
Ahora bien, de acuerdo con Hall y Klitgaard (2012) al analizar el comportamiento económico y productivo de las sociedades modernas debería ser de común aceptación que la energía es un factor determinante para todos los procesos productivos y sociales y que resulta ser tanto o más importante que el capital o el trabajo. En ese sentido, Kümmel (2011) afirma que sin los volúmenes de energía que demandamos diariamente se necesitaría una economía esclavista de dimensiones absurdas con el fin de proporcionar a los ciudadanos los bienes y servicios a los que se han acostumbrado. Por esta razón, desde sus primeros trabajos, este autor sostiene que la energía es un tercer factor productivo, el cual puede introducirse en la función de producción para cuantificar su aporte al PIB.
Esta aproximación a la realidad es consistente con lo que Smil (2005) denomina ‘sociedades energético-intensivas’, en las cuales se verifica que, desde que se tienen registros, el nivel de ingreso per cápita es directamente proporcional al nivel de consumo de energía per cápita5. Así, a pesar del creciente número de investigaciones donde se demuestra la importancia económica relativa de la energía para la generación de riqueza, su naturaleza como factor de producción no es considerada o no puede ser entendida6 en todas sus dimensiones por el análisis económico neoclásico7.
En la realidad, la estructura y el funcionamiento del aparato productivo y del sistema económico de los países industrializados (y de manera lógica también de los países en vías de desarrollo) resultan estar determinados por la necesidad de acceso permanente, eficiente y económico a diferentes vectores energéticos como son el petróleo, el carbón o el gas natural, entre otros. Esta necesidad constituye uno de los logros más importantes de las economías de mercado y es denominada seguridad energética, la cual es fundamentalmente responsabilidad del Estado.
Según Kümmel (1980, 1982), Kümmel et al. (1985) y Lindenberger et al. (2017), dichos vectores energéticos se convierten en un factor de producción en el momento exacto de su liberación de los portadores de energía, es decir, cuando el carbón es utilizado para la producción de energía eléctrica en las centrales termoeléctricas o cuando se quema en los altos hornos para la producción de acero, hierro o cemento, para citar solo algunos ejemplos específicos.
En este contexto, el modelo LINEX -entendido como una variante del clásico modelo Cobb-Douglas de la teoría estándar- desarrollado conceptual y empíricamente por R. Kümmel y los autores que han trabajado con él, y empleado rigurosamente por Ayres y Warr (2005, 2009), es el método más claro y funcional para realizar dicha aproximación. En consecuencia, este modelo es tomado como referente básico para su validación e implementación en el caso de Colombia. Lo anterior, con el objetivo inicial de cuantificar el aporte de la variable energética y su componente exergética en el proceso de crecimiento económico y para verificar su potencialidad explicativa, en comparación con los factores tradicionales de la función de producción neoclásica. A partir de esta verificación se busca explicar de manera alternativa e integral la estructura y evolución del PIB, es decir, del proceso de creación de riqueza, pero esta vez para el caso de una economía en vías de desarrollo.
Así, el principal objetivo de este ejercicio es constatar que los avances conceptuales y empíricos logrados con el modelo LINEX pueden ser extendidos y verificados para el caso de una economía de tamaño medio como es el caso de Colombia. Superando algunas de las dificultades de información existentes8, fue posible calcular una serie de energía (exergía)9 eléctrica, a partir de la cual se busca verificar su validez estadística, y calcular su peso en la determinación del PIB para Colombia durante el periodo de tiempo analizado10. Lo anterior se realizó en función de rigurosos análisis estadísticos previos que incluyen el uso del algoritmo de Levenberg Marquardt el cual permite resolver un problema de mínimos cuadrados no lineales con condiciones de frontera no lineales y expresadas en forma de desigualdades en función del cual fue posible validar tanto el modelo propuesto como sus presupuestos teóricos y conceptuales.
El cuerpo de este trabajo se desarrolla en tres partes: en la primera se tratan y explicitan los factores de producción y su proceso de agregación; en la segunda se introduce el factor (E) tanto en la función clásica Cobb y Douglas, como en la función LINEX. Finalmente, en la tercera parte se discuten los resultados del ejercicio y se consignan las conclusiones para el caso de Colombia.
I. Los factores de producción y su agregación
Las dos funciones de producción consideradas en este trabajo están sujetas a los dos elementos básicos del proceso de producción industrial: la ejecución de trabajo y el procesamiento de información. De esta observación se obtienen los principios de agregación que permiten resumir a nivel macroeconómico el conjunto heterogéneo de entradas y salidas de cada función. En resumen, y concordancia con el enfoque analítico tradicional, las variables empleadas son11:
-
El producto interno bruto (PIB) corregido por la inflación (Y) (Grupo de Estudios del Crecimiento Económico -GRECO-, 2004, p. 21).
-
El capital real agregado disponible corregido por la inflación (K). Comprende los desembolsos en concepto de adiciones a los activos fijos de la economía más las variaciones netas en el nivel de los inventarios. Variable medida y agregada en millones de pesos colombianos (GRECO,2004).
-
La población económicamente activa (L). Esta variable se define como las personas en edad de trabajar, que trabajan o están buscando empleo. En el presente estudio se usa el total de personas en edad de trabajar que trabajan como proxy de esta población (GRECO, 2004).
-
El consumo final de energía eléctrica (E) expresada en base exergética, el cual se presenta de manera agregada y medida en terajoules-año (TJ/año).
Resulta importante definir la siguiente notación:
II. Funciones de producción consideradas
En esta sección del documento se presentan las diferentes funciones de producción consideradas.
A. Exergía en el modelo de crecimiento de CobbDouglas
En el modelo tradicional de Cobb-Douglas, los factores de producción asociados al capital, la población económicamente activa y la exergía (K t , L t , E t ) son considerados como variables independientes (Ayres & Voudouris, 2014). La suposición es que alguna combinación de estas variables puede explicar los cambios en el PIB (Y t ) de Colombia durante un largo período de tiempo. El modelo considerado es el siguiente
donde A t es una medida de innovación usualmente denominada “progreso tecnológico”. La condición de rendimientos constantes implica que
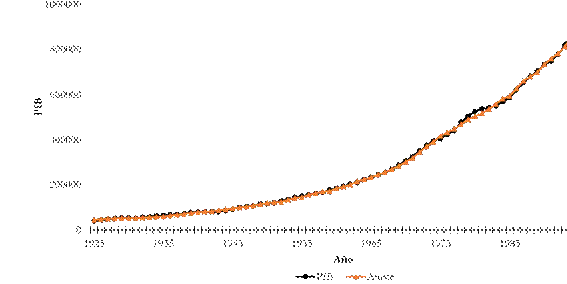
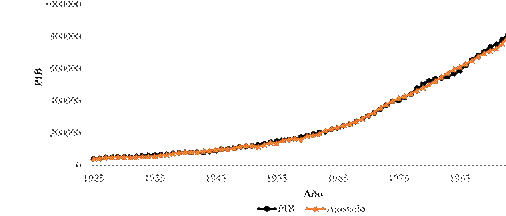
En la Figura 1 se puede observar que el crecimiento en el consumo de energía eléctrica en el país ha aumentado de manera acelerada a partir de los años 60, a una tasa que sobrepasa considerablemente la obtenida para los demás factores considerados. Nótese que dicho crecimiento es tan acelerado que oculta el crecimiento de los demás factores considerados en el estudio. Con el fin de que el lector pueda observar el crecimiento del PIB, el capital y la PEA se presenta, en la Figura 2, el índice (1925:1) de los factores de producción en Colombia incluyendo y excluyendo el consumo de energía eléctrica durante el periodo de tiempo considerado.
Figura 1
Índice 1925:1 del PIB y los factores de producción (Colombia, 19251997)
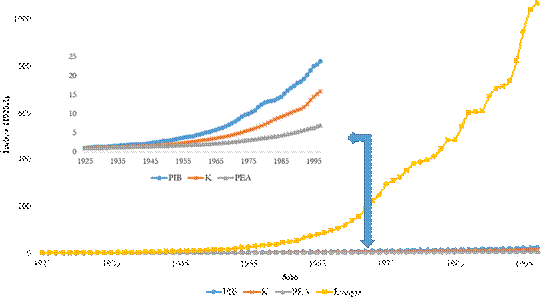
Fuente: elaboración propia.
Según Kümmel et al. (1985) y Ayres y Warr (2005, 2009) las soluciones más simples (triviales) para la condición de rendimientos constantes establecidas en la ecuación (2) son valores numéricos de la forma α = α 0, β = β 0 y γ 0 = 1 − α 0 − β 0. Para el caso de una economía de dos factores, se obtiene la función Cobb-Douglas original, donde γ 0 = 0. En el caso colombiano se toman como referencia los resultados presentados por el GRECO del Banco de la República, en los que se puede observar que la participación promedio durante el periodo 1926-1994 fue de 0,38225 y 0,61775 para α 0 y β 0, respectivamente (véase GRECO, 2004, p. 56).
Figura 2
Índice 1925:1 del PIB real y los factores de producción sin incluir el crecimiento del consumo de energía eléctrica (Colombia, 19251997)
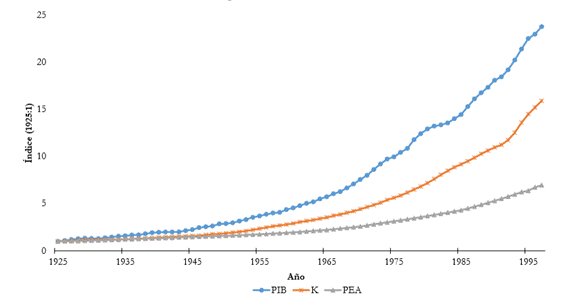
Fuente: elaboración propia.
La Figura 3 presenta claramente que la función Cobb-Douglas -sin considerar la exergía como tercera variable independiente, pero manteniendo la condición de rendimientos constantes y con elasticidades proporcionales a la participación en los pagos a los recursos de entrada en las cuentas nacionales- no explica el crecimiento histórico de Colombia en el largo plazo, pues se puede observar que los residuales del modelo ajustado crecen de forma exponencial.
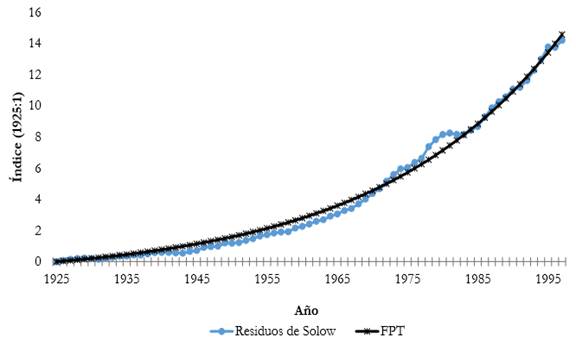
Volviendo al modelo estándar de Solow, y los supuestos que le acompañan, el factor A t se ajustó de forma independiente al residuo no explicado que una vez fue llamado “progreso tecnológico” o, más recientemente, la productividad total de los factores (PTF). En el presente trabajo se determinó que el “mejor ajuste” para la función de progreso técnico en Colombia durante todo el período 1925-1997 (que se muestra en la Figura 4) está dado por la siguiente expresión:
donde t es el año.
Figura 3
PIB vs ajuste modelo CobbDouglas con elasticidades fijas L (0,61775), K (0,38225) y E (0)
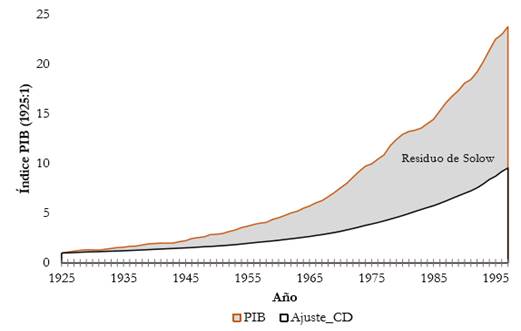
Fuente: elaboración propia
B. Exergía en la función de producción LINEX
Según Kümmel (1980, 1982) y Kümmel et al. (1985), las expresiones matemáticas para las elasticidades de producción α,β y γ, basándose en condiciones de límite asintóticas, deben satisfacer la condición de
Euler y ser funciones homogéneas de orden cero de las variables independientes. Siguiendo
la notación propuesta en Kümmel et al. (2002) todos los factores de producción considerados
están en unidades normalizadas a un año base. Considerando 1925 como periodo de referencia,
se tiene que
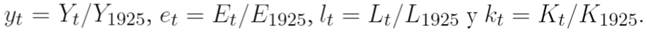
La primera de las soluciones, propuestas por las referencias mencionadas previamente, se establece como una forma de la ley de rendimientos decrecientes de capital. Se trata de una condición límite asintótica que trae la noción de que incluso en un estado futuro hipotético de uso intensivo de capital, en la que todos los productos son producidos por máquinas, se mantendrá alguna necesidad irreductible de trabajo L y exergía E, la cual expresan de la siguiente manera:
La segunda ecuación refleja la continua sustitución de trabajo por capital y exergía a medida que la intensidad de capital aumenta (automatización):
El supuesto de rendimientos constantes a escala implica que, en cada momento en el tiempo,
que es la condición de retornos constantes. La integración parcial de la ecuación de crecimiento produce la función llamada LINEX (linealexponencial):
donde y 0 es una constante de integración que mide la valoración monetaria promedio de la canasta original de bienes y servicios que componen la unidad de salida. Las funciones del tiempo a t y c t han sido caracterizadas por Kümmel (1980, 1982) y Kümmel et al. (1985) como “la eficiencia del capital” y “la demanda de energía”, respectivamente. Lo que resulta interesante son las productividades dependientes del tiempo que muestran un aumento significativo en la productividad exergética y la disminución de la productividad del trabajo en el tiempo en Colombia12.
Al comparar las funciones de producción para el PIB, la función Cobb-Douglas de la ecuación (1) y la función de LINEX en la (6), se puede obtener una expresión para el multiplicador A t en la ecuación (1), en términos de K,
L y E:
siendo α 0 y β 0 la participación promedio del capital y el trabajo durante el periodo 1926-1994, respectivamente (véase GRECO, 2004, p. 56). En la ecuación (7) se puede observar que A(t) es una expresión que depende fuertemente de E y débilmente (e inversamente) de K y L. Por lo tanto, si el modelo en (6) se ajusta razonablemente a los datos del PIB de Colombia, A t puede ser considerado como una función de la eficiencia de los recursos de conversión empleados en el proceso productivo.
III. Resultados
Los datos utilizados en este estudio corresponden a observaciones anuales del PIB corregido por la inflación (Y)13, el capital real agregado disponible (K)14, la población económicamente activa (L) expresada a través del número de personas empleadas al año y el consumo final de energía eléctrica (E) expresada en base exergética; agregada y medida en terajoules por año (TJ/año). Los datos del PIB, el capital real agregado disponible (K) y la población económicamente activa (L) se obtuvieron de los resultados reportados por el grupo de investigación del Banco de la República (GRECO, 2004), mientras que los datos del consumo final de energía eléctrica (E) en base exergética fueron producidos por una parte del equipo de investigación entre 2012 y 2013. La periodicidad de las series temporales es anual y se consideraron los registros de 1925 a 1997.
A. Modelo de crecimiento estándar: CobbDouglas
En esta subsección se considera el procedimiento presentado en Ayres y Warr (2005, 2009), el cual consiste en ajustar el modelo Cobb-Douglas para las series de tiempo consideradas en este estudio, la productividad total de los factores y la restricción de que la suma de las elasticidades es igual a uno. El modelo de regresión por ajustar se obtiene al aplicar logaritmo en ambos lados de la igualdad en la ecuación (1):
Finalmente, bajo la condición de rendimientos constantes (γ = 1−α−β), se obtiene lo siguiente:
En la ecuación anterior, A t es la medida de innovación denominada
“progreso tecnológico” y que se presenta en la Ecuación (1), y ε denota el término de error en el ajuste del modelo Cobb-Douglas. Despejando log (E t ) y agrupando términos semejantes en (8) se obtiene el siguiente modelo de regresión:
Por lo tanto, para garantizar la condición de rendimientos constantes se debe ajustar el modelo de regresión lineal múltiple (MRLM), empleando como método de optimización la minimización de la suma de cuadrados del error (SSE) (véase Ayres & Warr, 2005). En este modelo, la variable respuesta será log(Y t )−log(E t ), denotada log Y E, y sus covariables serán log(K t )−log(E t ), denotada log KE, y log(L t ) − log(E t ), denotada log LE. Los resultados obtenidos para el caso colombiano se presentan en la Tabla 1.
En la Tabla 1 se puede observar que todas las elasticidades obtenidas por el modelo Cobb-Douglas y sus covariables son estadísticamente significativas, es decir, aportan a la explicación de la variable respuesta (LogPIB). En la Tabla 2 se presentan las elasticidades estimadas y sus respectivos intervalos de confianza del 95 %:
Tabla 1
Pruebas individuales de los coeficientes del modelo de regresión ajustado
Tabla 2
Estimación puntual y por intervalos de las elasticidades - modelo CobbDouglas
| Parámetro | Valor estimado | Límite inferior | Límite superior |
|---|---|---|---|
| α | 0,2214 | 0,0673 | 0,3755 |
| β | 0,4858 | 0,3393 | 0,6323 |
| γ = 1-α-β | 0,2927 | 0,0000 | 0,5933 |
En la Figura 5 se presenta una comparación entre el PIB real colombiano (COP, miles de millones) y los valores estimados de esta serie empleando el modelo Cobb-Douglas en la ecuación (9). Se puede apreciar que las estimaciones realizadas por el modelo toman valores muy cercanos al PIB real colombiano hasta mediados de los años 70. A partir de este periodo el ajuste del modelo Cobb-Douglas se empobrece considerablemente. Los resultados obtenidos en esta subsección parecen indicar que, bajo el modelo tradicional, el consumo de energía eléctrica (E) en Colombia contribuye de manera significativa en el crecimiento económico del país; esto contradice los resultados tradicionales de una economía basada en dos factores.
B. Modelo de crecimiento alternativo: LINEX
Siguiendo el modelo LINEX presentado en Kümmel et al. (2002), tenemos que
en donde yt = Yt/Y1925, et = Et/E1925, lt = Lt/L1925, kt = Kt/K1925 son las variables macroeconómicas indexadas respecto al año base (1925). Los coeficientes a t y c t están dados por:
En las ecuaciones (11) y (12), a
1
,...,a
4
,c
1
,...,c
4 son parámetros positivos que se estiman minimizando la distancia cuadrática,
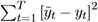 es decir, la diferencia cuadrática entre el valor estimado del PIB, empleando el
modelo LINEX (y˜
t
), y su valor real (y
t
). En el proceso de estimación se empleó el método de optimización no lineal de Levenberg-Marquardt,
bajo el supuesto de elasticidades de producción no negativas, para ajustar la función
de producción basada en el modelo LINEX.
es decir, la diferencia cuadrática entre el valor estimado del PIB, empleando el
modelo LINEX (y˜
t
), y su valor real (y
t
). En el proceso de estimación se empleó el método de optimización no lineal de Levenberg-Marquardt,
bajo el supuesto de elasticidades de producción no negativas, para ajustar la función
de producción basada en el modelo LINEX.
En la Figura 6 se presenta el valor anual de los polinomios a t y c t enunciados en las ecuaciones (11) y (12) y calculados para el caso colombiano durante el periodo de tiempo considerado 1925-1997.
Figura 6
Polinomios a(t) y c(t) del modelo LINEX para Colombia (19251997)
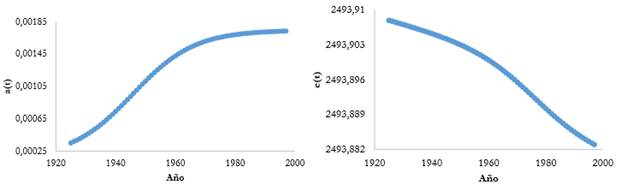
Fuente: elaboración propia.
En la Figura 7 se presenta el valor anual de las productividades marginales de α, β y γ (elasticidades de producción) para el caso colombiano durante el periodo comprendido entre 1925 y 1997. En este gráfico se puede observar un quiebre estructural en las pendientes de las curvas β y γ algunos años antes de 1935; este quiebre puede estar asociado a la marcada transición en el modelo económico de desarrollo del país15 y el rápido ritmo de crecimiento industrial, que se convirtió en un hito inigualable en el resto de América Latina y en la historia posterior del país (véase Aspe, Dornbusch & Obstfeld, 1983, p. 5-40). Una descripción detallada del panorama económico y político de Colombia durante los años 30 se puede encontrar en Ocampo y Montenegro (1982).
Figura 7
Elasticidades estimadas por el modelo LINEX para Colombia (19251997)
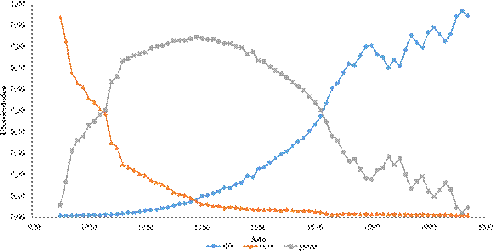
Fuente: elaboración propia.
Las elasticidades promedio obtenidas por el modelo LINEX para Colombia durante el periodo 1925-1997 fueron:
-
α = 0,3619: promedio asociado al capital real agregado disponible.
-
 β = 0,1359: promedio asociado a la población económicamente activa.
β = 0,1359: promedio asociado a la población económicamente activa.
-
γ = 0,5022: promedio asociado al consumo de energía eléctrica.
Desde la perspectiva macroeconómica y del equilibrio general, los resultados obtenidos se pueden interpretar en el sentido que el factor de pago asociado a la energía eléctrica (E) en Colombia y registrado en las cuentas nacionales ha sido mayor que el del capital (K) y la población económicamente activa (L), durante el periodo de tiempo considerado. Sin embargo, los economistas ortodoxos podrían decir que en Colombia los pagos a los factores de producción capital (K), trabajo (L) y energía (E) se desvían dramáticamente de los de los países de la OCDE, o que las elasticidades de producción de este manuscrito deben ser tan erróneas como las obtenidas por Kümmel, Ayres y todos los autores que han contribuido al desarrollo del modelo empleado en este trabajo.
Sin embargo, creemos que nuestros resultados confirman los hallazgos de los autores previamente mencionados, a saber, que la elasticidad de la variable energía es mucho mayor y que la de la mano de obra es mucho menor que los costos compartidos respectivos de estos factores. En consecuencia, los resultados obtenidos permiten validar el modelo empleado en el caso de Colombia y concluir que la condición de rendimientos constantes de la función de producción neoclásica no se aplica a ninguna de las economías que se han estudiado hasta ahora con esta innovadora metodología.
Finalmente, en la Figura 8 se presentan los valores ajustados por el modelo LINEX en comparación con los datos reales del PIB. Se puede apreciar que las estimaciones realizadas por el modelo toman valores muy cercanos al PIB real colombiano hasta inicios de los años 90. A partir de este año el ajuste del modelo LINEX se empobrece considerablemente.
Conclusiones
Si bien las investigaciones para formalizar una conexión entre la economía y la energía llevan varias décadas, ahora tenemos la posibilidad de relacionar la teoría del crecimiento económico con la variable energética con importantes resultados, independientemente del método empleado. En general, los análisis existentes revelan un creciente interés por establecer relaciones, formular metodologías y realizar rigurosos ejercicios para comprender, cuantificar y analizar las implicaciones de la producción y uso de la energía en las economías modernas. Desde la perspectiva heterodoxa con la inclusión de la energía como un tercer factor en la función de producción estándar se están logrado importantes resultados como revela el análisis realizado para el caso de Colombia una vez aplicado el modelo LINEX al análisis del crecimiento en el periodo de estudio.
En efecto, de una parte los resultados encontrados para Colombia permiten verificar que aunque en el modelo Cobb-Douglas ajustado todas las elasticidades obtenidas y sus variables regresoras asociadas son estadísticamente significativas; es decir, aportan en la explicación de la variable respuesta (LogPIB), al realizar la verificación de los supuestos del modelo se determinó que ninguno se cumple, lo cual implica que los resultados obtenidos por el mismo están considerablemente sesgados y no reproducen la verdadera relación entre el PIB con el capital, la población económicamente activa y el consumo de energía eléctrica.
En el caso del modelo alternativo LINEX (véase Figura 7), se encuentra que los resultados con los factores de producción considerados tienen un comportamiento concordante con lo presupuestado en dicho modelo, demostrando al menos tres hechos fundamentales: primero, que la participación de la energía eléctrica fue la fuente más importante de creación del PIB nacional en el periodo analizado. Segundo, que el aporte del capital fue ganando importancia hasta convertirse en el principal factor de creación del PIB, especialmente desde mediados de los años 70 del siglo XX. Y tercero, que la participación de la fuerza laboral en la composición del PIB disminuyó, especialmente desde los años 40, hasta aparecer marginalmente al final del periodo analizado. Estos resultados son interesantemente similares a los obtenidos por Lindenberger et al. (2017) para la economía estadounidense y alemana durante un periodo de tiempo muy similar al estudiado para el país.
En consecuencia, es claro que existe una metodología alternativa que permite explicar el crecimiento económico en el país, con arreglo a un modelo que, si bien no es conocido en nuestro medio, sí resulta potencialmente poderoso para explicar el proceso de creación de riqueza material desde una perspectiva de investigaciones de frontera. Estas investigaciones combinan el conocimiento de diferentes disciplinas y, además, permiten dinamizar el análisis del crecimiento económico en la medida que posibilitan ver la evolución en el tiempo y la participación de las elasticidades asociadas con las variables estándar (K) y (L) y la variable nueva (E), es decir, para nuestro análisis la energía (exergía) eléctrica.
Con todo, parece necesario profundizar en porqué la participación de la energía eléctrica (E) en la creación de riqueza fue más importante desde inicios del periodo y hasta los años setenta del siglo XX y en por qué disminuye desde entonces hasta el fin del periodo analizado. En principio, este resultado sugiere que si bien durante el primer subperiodo la energía eléctrica (E) resultaba determinante de la creación de riqueza (Kalmanovitz, 2010, p. 132), con la rápida urbanización del país, impulsada desde mitad del siglo XX, y el menor peso específico del aparato industrial en la creación y composición del PIB, dicha participación en la creación de riqueza empezó a decrecer también como consecuencia de la mejora en la eficiencia de los aparatos empleados por las industrias y los consumidores en general, la cual ha ido aumentando, justamente desde los años 80 del pasado siglo XX.
También resulta interesante observar cómo desde los años setenta el capital (K), empezó a repuntar como el principal factor de producción en la economía colombiana, lo cual refuerza la tesis de la urbanización del país y de la modernización al menos de algunos sectores productivos representativos.
Aunque no son concluyentes, dichos resultados representan un efecto combinado sobre la economía colombiana y derivado del impacto negativo de la llamada crisis energética; los esfuerzos para modernizar la base industrial y productiva del país, factores que explican, al menos parcialmente, el cambio de tendencia en la participación del capital y la energía.
Sin embargo, esta situación resulta paradójica en el sentido de que durante estos años el país realizó grandes inversiones en infraestructura eléctrica, en un proceso que permitió la construcción de un importante número de proyectos de generación de energía eléctrica e inversiones intensivas en capital. Dichas inversiones fueron realizadas en un contexto donde al tiempo que la industria se estaba debilitando, la urbanización del país se estaba consolidando.
Con todo, será necesario profundizar y ahondar en este análisis del papel de la energía en el proceso productivo, para lo cual será necesario ampliar tanto la base de información relativa a la contribución energética y exergética, así como en las demás variables las cuales deben ser obtenidas y validadas estadísticamente en diferentes intervalos de tiempo.
Finalmente, cabe decir que si bien el trabajo de Kümmel y los autores relacionados con esta metodología han llevado el debate relativo a los determinantes del crecimiento económico a un punto muy interesante en relación con el paradigma dominante, sus proyecciones apuntan a analizar el resultado de esta realidad en función de fenómenos tan complejos como el cambio climático y la sostenibilidad del desarrollo económico y social, en la medida que estos procesos dependen hasta ahora de los recursos que más contaminan la atmosfera. Será necesario entonces lograr mayores niveles de eficiencia, tanto en la producción como en el consumo de energía, si se quiere lograr mantener los actuales estándares de vida sin afectar de manera irreversible el medio natural en el que vivirán las generaciones futuras.