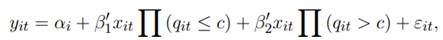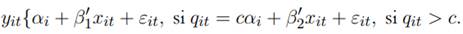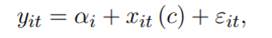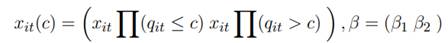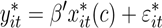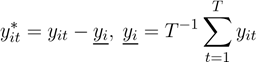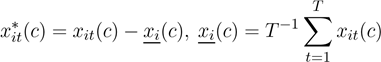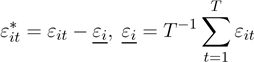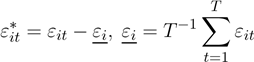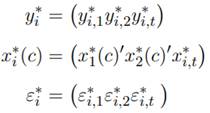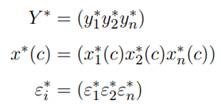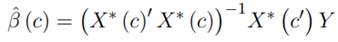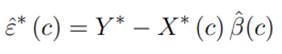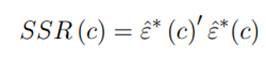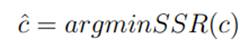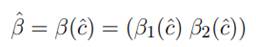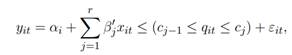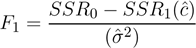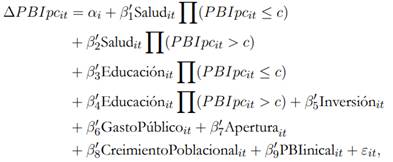Introducción
El estudio empírico de los determinantes del crecimiento económico sigue planteando interrogantes a pesar de la extensa literatura existente en el área. Entre otras cosas, se debaten dos cuestiones fundamentales. Primero, la sensibilidad de los resultados a la forma funcional que adopta la relación entre el crecimiento y los factores explicativos. Segundo, la relevancia de dichos factores en la definición del desempeño de los países. Lo cierto es que si la relación funcional asumida no es la correcta se estaría incurriendo en un error de especificación, y en tal caso ciertas variables podrían mostrarse como no significativas cuando en realidad lo son.
El abordaje del capital humano como fuente de crecimiento no es ajeno a tales controversias. La teoría del capital humano indica que todas aquellas inversiones destinadas a mejorar la capacidad humana incrementan la productividad de una economía. Desde las contribuciones de Lucas (1988), Romer (1990) y Mankiw, Romer y Weil (1992), poco se debate la relevancia teórica del capital humano como elemento explicativo del crecimiento, junto con la acumulación de capital físico y las mejoras tecnológicas.
Tampoco parecían suscitarse dudas desde el trabajo empírico: a partir de los seminales aportes de Barro (1991) y Mankiw et al. (1992), innumerables fueron los desarrollos que mostraron una clara relación positiva entre la salud, la educación y el crecimiento económico.
Sin embargo, hacia inicios del presente siglo se generaban las primeras controversias al respecto. Pritchett (1999) mostró que altos niveles de inversión en educación desde los años 60 parecían haber generado un escaso crecimiento en países en desarrollo (no así, en países desarrollados). Contribuciones empíricas más recientes han sido críticas en focalizar al capital humano como un componente relevante del crecimiento económico (Henderson, Papageorgiou y Parmeter, 2012; Delgado, Henderson y Parmeter, 2014).
Por otra parte, Temple (2001), Durlauf, Johnson y Temple (2005), Kourtellos (2011), Sunde y Vischer (2015), Rojas, Monterubbianesi y Dabús (2019), entre otros, insisten en que las variables representativas del capital humano sí revisten importancia. En tal sentido, existe un consenso mayoritario en la literatura a favor de una relación significativa entre capital humano y crecimiento (Durlauf et al., 2005; Bucci, Prettner y Prskawetz, 2019).
Una cuestión fundamental del debate es que se han propuesto tantas variables explicativas del crecimiento como países con datos se encuentran disponibles (Durlauf et al., 2005 ). Sería muy difícil determinar cuáles son las verdaderamente importantes si se incluyeran absolutamente todas en un mismo estudio. A la hora de tomar una decisión en cuanto a la formulación empírica, el investigador no debe descartar los desarrollos teóricos ni la interpretación intuitiva. En este sentido, considerando la salud y la educación como componentes clave del capital humano, se puede plantear que la salud determina la capacidad que cada individuo tiene para desarrollar su potencial físico y cognitivo, mientras que la educación incrementa el nivel de conocimiento y habilidad. Ambos componentes fructifican el esfuerzo humano, pudiéndose traducir en mayor productividad global, así como en mayores salarios a nivel individual (Schults, 1961; Nafukho, Hairston y Brooks, 2004; Becker, 2007).
Por otro lado, la no observación de un efecto claro de la educación y la salud sobre el crecimiento económico puede deberse a errores de especificación. Los modelos paramétricos lineales derivados del planteo teórico de Solow-Swan preestablecen una relación funcional entre las variables explicativas y la tasa de incremento del producto1. Esto supone que el stock de capital humano tiene siempre el mismo efecto sobre el crecimiento, tanto a lo largo del tiempo como en diferentes países. Estas metodologías podrían no reflejar la complejidad de la relación en cuestión.
Precisamente, el argumento de que el capital humano impacte del mismo modo en todas las economías ha sido cuestionado a partir de los trabajos de Azariadis y Drazen (1990) y Durlaf y Johnson (1995). Si el capital humano afecta al crecimiento de una forma no lineal, su contribución podría modificarse una vez que la economía supera cierta masa crítica de producto y capital físico (nivel umbral) a partir de la cual el aprovechamiento de efectos externos conduciría a un incremento sustancial en la tasa de crecimiento. En tal caso, las estimaciones paramétricas lineales no serían capaces de capturar la evolución cambiante de la relación entre capital humano y crecimiento. Para justificar esta idea desde un punto de vista teórico, Azariadis y Drazen (1990) introdujeron discontinuidades en la función de producción agregada. Esta discontinuidad implica la presencia de niveles umbrales y diferentes estados estacionarios.
Es decir, el capital humano podría mostrar rendimientos decrecientes o no decrecientes según el nivel de ingresos y capital per cápita en que se encuentre la economía. Finalmente, el estado estacionario al que arribe una economía dependerá de si su nivel de capital humano y producto per cápita inicial se encuentran por encima o por debajo de cierto umbral.
Específicamente, Azariadis y Drazen (1990) analizan el caso de un umbral y dos estados estacionarios, aunque -como se verá en este trabajo- puede existir un número mayor de umbrales. El tratamiento de no linealidades permite una aproximación más amplia y realista en el estudio de países con diferentes características y, en particular, con distinto nivel de desarrollo e ingreso per cápita. A su vez, el hecho de desagregar el capital humano en dos componentes fundamentales, salud y educación, permite llevar a cabo un estudio más desagregado y preciso de la influencia del capital humano sobre el crecimiento.
De este modo, a fin de aportar nueva evidencia sobre el tema, el objetivo del presente trabajo es analizar la existencia de efectos umbral mediante una aproximación no lineal en la relación salud-crecimiento y educación- crecimiento. Se busca determinar la existencia y cantidad de umbrales, así como el nivel de dichos puntos de inflexión, a partir de los cuales la relación capital humano-crecimiento mostraría un cambio en el comportamiento observado.
La contribución del trabajo es en dos sentidos. Por un lado, corrobora la existencia de un efecto no lineal del capital humano sobre el crecimiento. Por otro lado, incorpora un concepto amplio de capital humano, al tomar en cuenta tanto la salud como la educación. Esto permite establecer diferencias en el comportamiento de la salud y de la educación con relación al crecimiento. Los resultados indican que mientras la salud es siempre favorable al crecimiento, la educación solo juega un rol relevante en economías con altos niveles de ingreso.
A continuación, se presenta la revisión de la literatura abocada al tratamiento de no linealidades en la relación capital humano-crecimiento. En la sección II se detalla la metodología utilizada y los datos. Los resultados se muestran y analizan en la sección III. Por último, se presentan las conclusiones y consideraciones finales.
I. Revisión de literatura
Uno de los primeros desarrollos empíricos de no linealidades que estudia la relación entre educación y crecimiento es el trabajo antes citado de Durlauf y Johnson (1995). Utilizando el método de clasificación y árboles de regresión, los autores rechazan la existencia de un único modelo lineal del tipo Solow-Swan como generador de datos para todas las economías. Existirían cuatro modelos lineales diferentes, uno para cada grupo de economías, establecidos en función de las condiciones iniciales. Los resultados revelan que la educación no es una variable significativa para explicar el crecimiento de los dos grupos de menores ingresos, pero sí posee un efecto positivo y significativo en los dos clúster de mayores ingresos.
Por otra parte, Liu y Stengos (1999) analizan no linealidades en el ingreso inicial y las tasas de escolarización. El trabajo también arroja evidencia a favor de regímenes múltiples. En particular, las tasas de matriculación secundaria se asocian a un mayor crecimiento si exceden el 15 %. El efecto sobre el incremento del producto tiende a disminuir a partir de tasas de matriculación del 75 %. Asimismo, Kalaitzidakis et al. (2001) encuentran efectos no lineales sobre el crecimiento económico utilizando años promedio de escolarización. A bajos niveles de capital humano, el efecto de este sobre el crecimiento es negativo, se torna positivo a niveles medios, y no significativo a niveles altos de ingreso. Por tanto, los autores concluyen que la evidencia es consistente con la idea de que existen umbrales a partir de los cuales el efecto del nivel de educación sobre el crecimiento se modifica, y de que puede diferir en función de qué posición inicial ocupe la economía. Temple (2001) arriba a resultados similares. Por medio de mínimos cuadrados recortados muestra que los coeficientes de las variables de escolarización son significativos sólo cuando se les permite tomar formas no lineales. Además, reconoce que el efecto sobre el crecimiento es pequeño.
Durlauf, Kourtellos y Minkin (2001) utilizan tasas de matriculación secundaria en un modelo semi-paramétrico de coeficientes suavizados, encontrando la presencia de no linealidades significativas del capital humano sobre el crecimiento condicional al ingreso inicial. Estos autores testean la homogeneidad en los parámetros, similar al testeo que habían realizado Durlauf y Johnson (1995). Es interesante notar que esta metodología plantea una diferencia conceptual al testeo de efectos umbral, dado que el supuesto básico es que los países se conducen bajo modelos lineales, aunque poseen distintas funciones de producción agregada.
Aunando las ideas de no linealidades y heterogeneidad de los parámetros, Masanjala y Papageorgiu (2004) sostienen que las primeras son las que explican la heterogeneidad de los parámetros que definen la ecuación de crecimiento. Mediante el uso de la metodología de umbral endógeno de Hansen (1999; 2000) -la cual permite analizar el efecto de cambios en ciertas variables independientes sobre la variable dependiente considerando diferentes rangos de valores de otras variables dependientes-, los autores determinan cuatro regímenes, utilizando alternativamente las variables de Producto Bruto Interno (PBI) per cápita inicial y tasa de alfabetización inicial para definir el nivel de los umbrales en un estudio de tipo crosssection. Siendo que los umbrales establecen cuatro grupos de países en función de sus condiciones iniciales, proceden a calcular mediante mínimos cuadrados no lineales los coeficientes para cada submuestra, encontrando significativas diferencias en los parámetros estimados. Además, en tres de los cuatro regímenes, encuentran que el efecto de la inversión en educación sobre el crecimiento es negativo. Adicionalmente, Mamuneas, Savvides y Stengos (2006) encuentran evidencia a favor de la especificación semiparamétrica versus las especificaciones lineales, y establecen que para un número considerable de países de ingresos medios los años de escolarización no exhiben un efecto significativo sobre el producto.
Posteriormente, mediante el uso de kernels estocásticos y metodologías no paramétricas localmente lineales, Maasoumi, Racine y Stengos (2007) concluyen que distintos grupos de economías no pueden ser analizados utilizando un mismo modelo de base. En este trabajo, los años promedios de escolarización de la población adulta muestran una relación creciente y positiva con el crecimiento en el grupo de las economías pertenecientes a la Organización para la Cooperación y el Desarrollo Económicos (OCDE), y exhiben un impacto tenue para los países no OCDE. Sin embargo, se encuentra una asociación general de bajo capital humano y bajas tasas de crecimiento en ambos grupos. Por su parte, Kourtellos (2011) concluye que los parámetros que definen la ecuación explicativa de la tasa de crecimiento dependen del nivel de alfabetización inicial y de la esperanza de vida inicial, lo que sería consistente con la presencia de equilibrios múltiples.
Sin embargo, Henderson et al. (2012) y Delgado et al. (2014) encuentran que las variables referidas a educación no juegan un rol importante para explicar el crecimiento aún bajo especificaciones no paramétricas. En el primer trabajo, los autores muestran que las tasas de fertilidad y la recíproca de la esperanza de vida al nacer sí afectan al crecimiento de forma no lineal y que los logros educativos medidos mediante mean test scores proveen una medida más confiable que años de educación.
Sanso-Navarro y Vera-Cabello (2015) y Peiró-Palomino (2016) analizan los determinantes del crecimiento de las regiones que integran la Unión Europea. También bajo la utilización de técnicas no paramétricas y varios kernel estocásticos obtienen evidencia de relaciones no lineales para la productividad laboral inicial, la dotación de capital humano y la de capital social. Más recientemente, Zidan (2019) divide la muestra de forma ad hoc por regiones geográficas y analiza, a partir de un modelo de selección de variables basado en el método bayesiano y de descomposición, cómo la diferencia de comportamiento entre países se debe a la diferencia en los parámetros estimados o en el nivel de las variables explicativas. Concluye que el capital humano (medido como años de educación) es una variable clave para el crecimiento de América Latina, no así para otras economías en desarrollo.
Analizando una muestra de 86 países durante el periodo 1960-2010 mediante estimaciones semi-paramétricas, Rojas et al. (2019) muestran que el estatus de salud y el nivel de educación exhiben una relación no lineal con el crecimiento. La evidencia encontrada en este trabajo indica que los efectos marginales del capital humano sobre el crecimiento poseen un comportamiento relativamente homogéneo entre países para el caso de los indicadores de salud, mientras que exhibe una gran dispersión de los rendimientos para la educación en los niveles medios y altos de ingresos, sugiriendo la presencia de efectos umbral. Finalmente, Kourtzidis, Tzeremes y Tzeremes. (2019) analizan la relación entre el gasto en salud y el cambio tecnológico. Mediante el cálculo de estimadores de eficiencia condicionada dependientes del tiempo, revelan que el efecto del gasto en salud per cápita sobre el cambio y el catch-up tecnológico no es lineal, sino que está sujeto a los niveles de ingreso de los países.
En resumen, existe una vasta literatura empírica que sugiere la existencia de efectos no lineales del capital humano sobre el crecimiento económico a partir de la presencia de parámetros heterogéneos y efectos umbral. Sin embargo, son escasos los trabajos que consideran el capital humano de forma más amplia, de modo que incluya ambos aspectos, estatus de salud y de educación, problema que se aborda a continuación.
Metodología y datos
A. Metodología
Los modelos de regresión con umbrales sostienen que las estimaciones individuales pueden ser divididas en clases de acuerdo con el valor de una variable observable. Hansen (1999; 2000) desarrolló la metodología de Threshold Regression Model, la cual posee una interpretación natural como modelo que testea la existencia de múltiples equilibrios al incorporar tanto los estimadores como los niveles umbrales. La metodología permite considerar simultáneamente las ventajas de los paneles de datos, las heterogeneidades entre países y las no linealidades con efectos de umbral (Seo y Shin, 2016).
En este trabajo, siguiendo a Hansen (1999; 2000), se estima un modelo de regresión con umbrales para datos de panel con efectos fijos (PTR model por sus siglas en inglés). Es un modelo de paneles no dinámicos con efectos fijos individuales. Así, la definición general del modelo para un conjunto de i individuos (países en el caso del presente trabajo) y t períodos de tiempo está dada por la ecuación (1).
donde y it es un escalar de variables endógenas, α i es el efecto fijo, q it es un escalar de variables umbral, el estimador x it es un vector de variables explicativas (se supone que existen k variables explicativas), β representan los coeficientes a estimar que indican el efecto de cada variable endógena sobre la∏ · variable exógena, ( ) es la función indicadora (es decir que define el valor de los coeficientes de la estimación de acuerdo al valor de las variables umbral), c es el parámetro umbral y ε un término de error aleatorio.
Dado que la función indicadora define conjuntos de valores que pueden tomar los parámetros β dependiendo del valor de las variables umbral, es posible reescribir la ecuación (1) así:
El modelo puede ser estimado por mínimos cuadrados no lineales (NLLS por sus siglas en inglés), para lo cual será necesario, tomando en cuenta la función indicadora, redefinir la función (2) como (3).
donde:
De este modo, las observaciones son divididas en dos regímenes dependiendo de si el valor de la variable umbral q it es mayor o menor que el umbral c. Estos regímenes se diferencian por las pendientes de la regresión β 1 y β 2.
En los modelos de efectos fijos, los efectos individuales para cada unidad α i no son observables, por lo cual deben ser eliminados para la estimación. Para ello, se aplica la transformación within, es decir se redefinen las variables como la distancia respecto a su media. De este modo, el modelo queda expresado de acuerdo con la ecuación (4).
Las variables indicadas con * representan la desviación respecto a su media, es decir:
A los fines de proceder con el desarrollo de la metodología y poder definir el estimador del modelo, resulta necesario introducir los componentes de las matrices que integran la ecuación (4):
Entonces, agregando los diferentes períodos de tiempo:
Para un umbral dado c, la pendiente β puede ser estimada mediante mínimos cuadrados ordinarios de acuerdo con la ecuación (5)
El vector de residuos vendrá dado por (6).
Y la suma de los residuos al cuadrado será, de acuerdo con la ecuación (7).
El umbral estimado cˆ se obtiene por la minimización de la suma de los residuos al cuadrado, tal como se define en (8)
Aquí radica una de las grandes fortalezas de la metodología, ya que permite estimar no sólo el valor de los coeficientes para cada tramo de la variable umbral, sino que también posibilita estimar endógenamente el valor de esos umbrales:
Dado cˆ puede estimarse, a partir de la ecuación (3), el valor de β como:
El modelo puede generalizarse considerando la existencia de r umbrales c 1 ,...,c r :
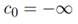 y
y
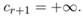
Hansen (1999) demuestra que, mediante el análisis de inferencia a través de un test F, es posible encontrar el número óptimo de regímenes. En este caso se consideran dos números alternativos de umbrales partiendo, en principio, de la hipótesis de no existencia de umbrales versus la existencia de un umbral, siguiendo por la existencia de un umbral versus dos umbrales, y así sucesivamente.
Por ejemplo, para el primer caso la hipótesis nula será H 0 = β 1 = β 2 y el valor del estadístico vendrá dado por (11).
En caso de rechazar H 0, quedaría en evidencia que las pendientes de los modelos estimados considerando la no existencia de umbrales y la existencia de un umbral difiere y, de esta forma, resulta necesario considerar la existencia de uno o más umbrales.
B. Datos
Con base a las contribuciones de Levine y Renelt (1992), Barro (1996) y Dabús y Laumann (2006), las variables de control incluidas en este trabajo son: nivel de inversión (en porcentaje del PBI), nivel de gasto público (aproximado por el consumo público, en porcentaje del PBI), grado de apertura (expresado como exportaciones más importaciones sobre PBI), crecimiento poblacional (expresado como la diferencia del logaritmo de la población entre dos períodos) y PBI per cápita al inicio de cada período (expresado en logaritmo). El resto de las variables explicativas de interés están determinadas por indicadores representativos del capital humano, los cuales se detallan a continuación.
Siguiendo a Kalaitzidakis et al. (2001), Durlauf et al. (2005) y Barro y Lee (2013), se toman los años promedio de escolarización como medida de educación. Específicamente, las proxies utilizadas son los años promedio totales de educación y años promedio de educación secundaria de la población mayor de 15 años (expresados en logaritmos). El estatus de salud es aproximado por la esperanza de vida al nacer y la inversa de un índice construido a partir de la tasa de mortalidad infantil (valor máximo de la muestra menos el valor del país particular), ambas variables consideradas en logaritmos. Se procede de esta manera teniendo en cuenta que se espera un efecto positivo del estatus de salud sobre el crecimiento y que la variable tasa de mortalidad infantil (TMI) es una proxy inversa del estatus de salud (una mayor mortalidad infantil se asocia a un menor status de salud). Finalmente, la variable explicada es la tasa de crecimiento del producto per cápita, definida como la variación del logaritmo del PBI per cápita. La Tabla 1 incluye la descripción de las variables, la fuente de datos utilizada en cada caso y el signo esperado de cada una de ellas en la estimación.
Tabla 1
Fuentes de las variables de la base de datos
| Variable | Descripción | Fuente | Signo esperado |
|---|---|---|---|
| Variación del PBI per cápita (∆PBIpc it ) | Tasa de variación del logaritmo del PBI per cápita de acuerdo con la Paridad del Poder Adquisitivo a partir del Índice de Laspeyres, expresado a precios constantes de 2005 | Tasa de variación estimada a partir de datos de la Penn World Table | Variable endógena |
| Educación (variable 1) (Educación it ) | Logaritmo de los años promedio de educación secundaria de la población mayor de 15 años | Barro y Lee (2013) | Positivo |
| Educación (variable 2) (Educación it ) | Logaritmo de los años promedio totales de educación de la población mayor de 15 años | Barro y Lee (2013) | Positivo |
| Salud (variable 1) (Salud it ) | Logaritmo de la esperanza de vida al nacer | UN data | Positivo |
| Salud (variable 2) (Salud it ) | Logaritmo de la inversa de la tasa de mortalidad infantil, calculada como la diferencia entre el valor máximo de la muestra y el valor del indicador para el país correspondiente | UN data | Positivo |
| Inversión (Inversión it ) | Proporción de inversión en el PBI expresado a precios constantes de 2005 | Penn World Table | Positivo |
| Gasto Público (Gasto Público it ) | Proporción de consumo del gobierno en el PBI expresado a precios constantes de 2005 | Penn World Table | Negativo |
| Apertura (Apertura it ) | Proporción de la suma de las exportaciones y las importaciones en el PBI expresado a precios constantes de 2005 | Penn World Table | Positivo |
| Crecimiento Poblacional (Crecimiento Poblacional it ) | Tasa de variación de la población | Tasa de variación calculada a partir de datos de la Penn World Table | Negativo |
| PBI inicial (PBI inicial it ) | Logaritmo del PBI per cápita rezagado un período de acuerdo con la Paridad del Poder Adquisitivo a partir del Índice de Laspeyres, expresado a precios constantes de 2005 | Penn World Table | Negativo |
La idea es determinar si, de acuerdo con el nivel de ingreso per cápita de los países, el efecto del estatus de salud y el nivel de educación sobre el crecimiento modifica su comportamiento, por lo que el PBI per cápita es la variable que se toma para detectar umbrales a partir de los cuales se encuentran dichos cambios. Así, el modelo a estimar, en los términos de la ecuación (1), queda establecido en la ecuación (12).
donde ∆PBIpc it es la tasa de crecimiento del producto per cápita, Salud it representa el estatus de salud, Educación it representa el nivel educativo, Inversión it identifica la participación de la inversión total en el producto, GastoPúblico it es la participación del consumo público en el producto, Apertura it es el indicador del grado de apertura de la economía, Crecimiento Poblacional it es la tasa de crecimiento de la población y PBIinicial it corresponde al valor del PBI per cápita al inicio del periodo.
Como se mencionó previamente (ecuación 10), el modelo propuesto puede posteriormente extenderse para considerar la existencia de más de un umbral y, por lo tanto, de más de dos regímenes. En ese caso, se tendrá un β de cada una de las variables de capital humano para cada régimen, es decir un valor del conjunto de parámetros estimados para cada rango de valores de PBI per cápita.
De acuerdo con la disponibilidad de datos, se construyó un panel de 86 países con observaciones quinquenales para el período 1960-2010. La Tabla 1A del anexo2 incluye la lista de los países incluidos en la estimación.
Todos los valores monetarios están expresados en dólares constantes del 2005. Las estimaciones fueron realizadas utilizando el software Stata y siguiendo el código desarrollado por Wang (2015), quien elaboró dicho código para permitir incorporar la metodología de regresión con efectos umbral presentada al software mencionado.
III. Evidencia empírica
Una primera aproximación al tema de la relevancia de los componentes del capital humano sobre el desempeño de la economía se muestra en la Figura 1. Los paneles (a) y (b) de la figura muestran los indicadores de niveles de educación (años promedio de educación de la población de 15 años y más, y años promedio de educación secundaria de la población de 15 años y más, respectivamente) con relación al PBI per cápita para todos los países en todos los años de la muestra. Los paneles (c) y (d) exhiben los indicadores de salud (esperanza de vida al nacer y tasa de mortalidad infantil, respectivamente) con relación al PBI per cápita.
Como era de esperar, se aprecia una relación claramente positiva entre los indicadores de educación y salud, medida a través de la esperanza de vida, y el PBI per cápita; y negativa entre la tasa de mortalidad infantil y el nivel de vida promedio de la población, aproximado por el PBI per cápita. Por supuesto, es necesario obtener evidencia más precisa sobre el tema.
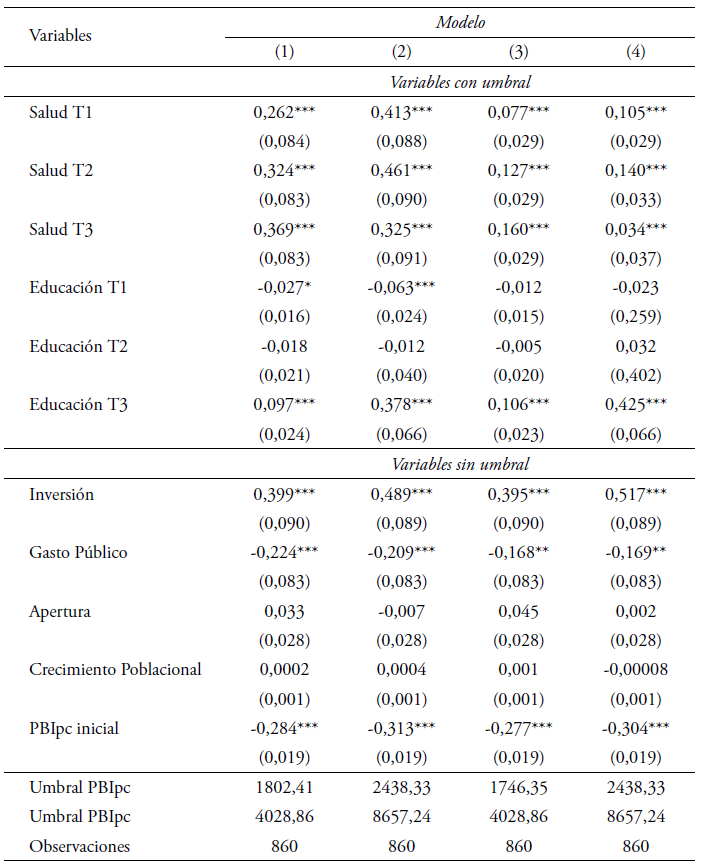
A tal fin, se realizaron estimaciones de la relación capital humanocrecimiento y se interpretaron los resultados obtenidos. Para probar la robustez de las conclusiones se trabajó con los dos indicadores de salud y educación alternativamente, construyendo cuatro estimaciones diferentes. Los modelos (1) y (2), señalados en las primeras dos columnas de la Tabla 3, tomando como variable proxy del estatus de salud a la esperanza de vida al nacer; mientras que los modelos (3) y (4) (columnas 3 y 4 de la Tabla 3), utilizan el indicador de mortalidad infantil. Por otra parte, como variables proxy de educación se utilizan años promedio de escolarización secundaria en los modelos (1) y (3), mientras que los modelos (2) y (4) consideran los años promedio de escolarización total.
Figura 1
Relación entre nivel de PBI per cápita e indicadores de capital humano
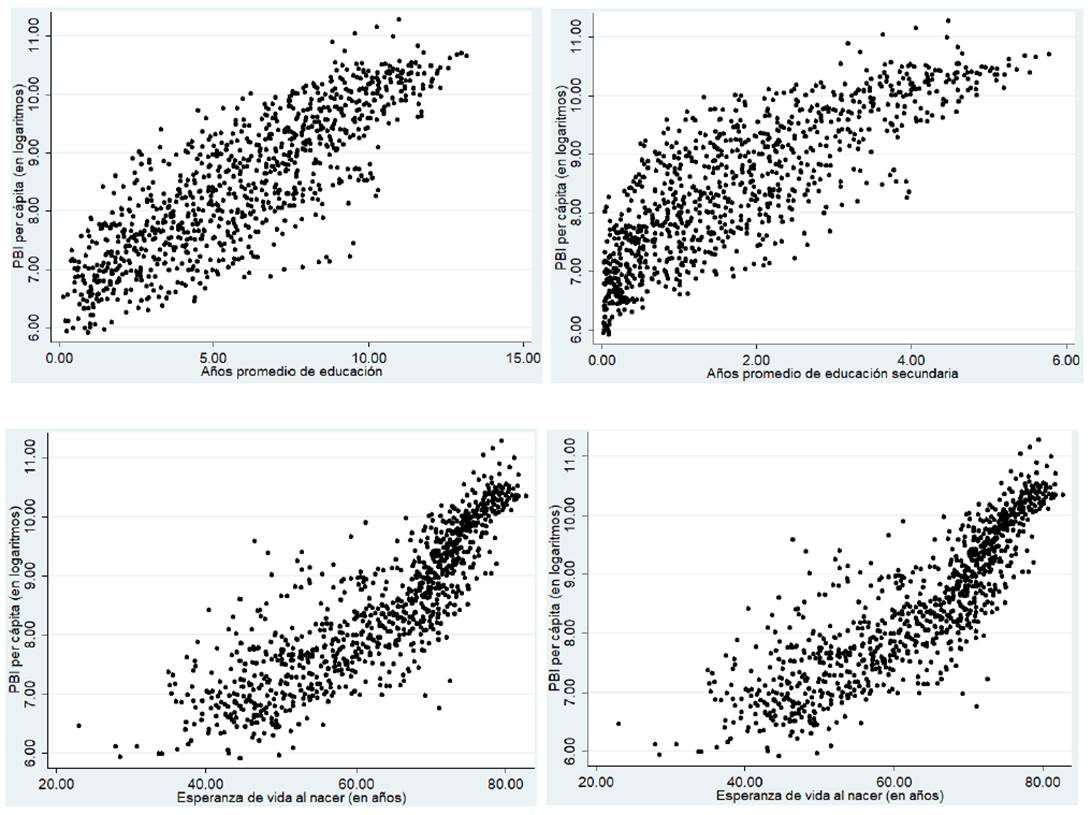
Fuente: elaboración propia, con base a datos de Barro y Lee (2013), Penn World Table (Feenstra, et al., 2015) y UNdata (2019).
Para tratar la potencial endogeneidad de las variables de capital humano respecto del crecimiento económico se realizaron estimaciones empleando variables instrumentales a través de la técnica de mínimos cuadrados generalizados en dos etapas (MCG2E), utilizando como instrumentos los rezagos (en uno y dos períodos) de las variables de salud y educación. Al analizar los resultados de los modelos con variables instrumentales y compararlos con los modelos originales mediante la aplicación la prueba de Hausman, se observó que los mismos no difieren estadísticamente, lo que indica que el problema de endogeneidad no es relevante en este caso, dando mayor robustez a los resultados obtenidos.
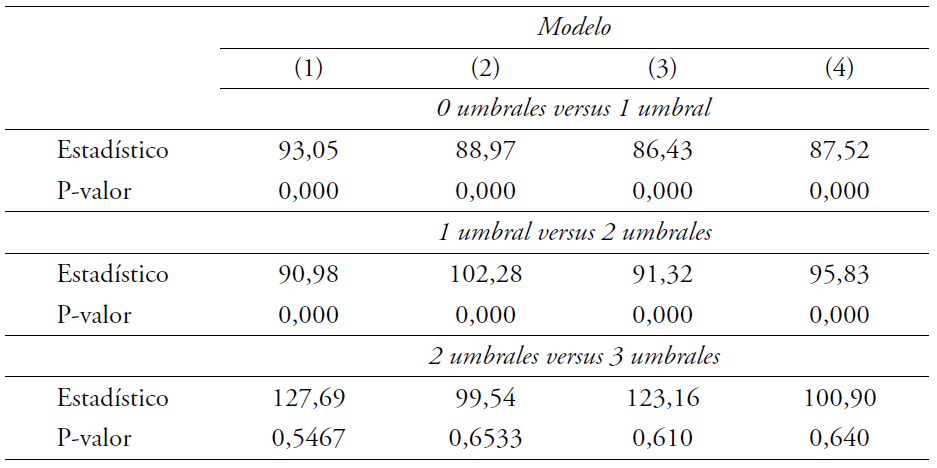
Para analizar el número óptimo de umbrales se realizó la prueba F de significatividad conjunta considerando la posible existencia de uno, dos o tres umbrales. En cada caso, para testear la existencia de k umbrales, la hipótesis nula es que los coeficientes considerando k − 1 umbrales y k umbrales son iguales. El análisis se realiza de forma secuencial. La Tabla 2 muestra los resultados de las pruebas. Mientras que se rechaza la hipótesis nula (igualdad en las pendientes de las variables de los modelos estimados) en el primer y segundo ejercicio, no se rechaza en el tercer caso para cualquiera de las cuatro estimaciones, lo que indica la existencia de dos umbrales determinados por el ingreso per cápita en la relación capital humano-crecimiento. Es decir, existen tres rangos de valores diferentes de PBI per cápita para los cuales el efecto de las variables de capital humano sobre el crecimiento económico tomará valores distintos.
Luego, la Tabla 3 presenta los resultados de las estimaciones para el modelo de dos umbrales. En esta se observa la existencia de dos puntos de inflexión asociados a disímiles niveles de ingreso per cápita. Esto implica que la relación capital humano-crecimiento difiere por encima y por debajo de dichos puntos, definiendo tres tramos de la función en donde los parámetros estimados que definen el proceso de generación de datos son heterogéneos.
Dependiendo de la especificación del modelo, el nivel de ingreso que determina el umbral más bajo toma valores entre 1800 y 2400 dólares, mientras que el siguiente umbral se encuentra entre los 4000 y 8500 dólares per cápita. Estos valores son particularmente sensibles a la variable de educación seleccionada, tomando los valores más altos al utilizar el indicador de años totales de educación. Así, los coeficientes de las variables de interés denominados con T1, T2 y T3 se asocian a cada uno de los tramos de ingresos per cápita inicial que se establecen entre los umbrales señalados. En los modelos (1) y (3) (es decir, cuando el estimador utilizado es años promedio de escolarización secundaria), los valores de los coeficientes nombrados con T1 corresponden a las economías con ingresos iniciales entre 0 y 1800 dólares; con T2 se nombran los coeficientes estimados para las economías con ingresos iniciales entre 1801 y 4000 dólares; y con T3, los coeficientes para aquellos países con ingresos iniciales superior a 4000 dólares. Por su parte, en los modelos (2) y (4) (cuando el estimador relevante es años promedio de escolarización total), T1, T2 y T3 señalan los coeficientes estimados para los países cuyos ingresos per cápita iniciales se encontraban entre 0 y 2400 dólares (T1), entre 2401 y 8000 dólares (T2) y por encima de 8000 dólares (T3), respectivamente.
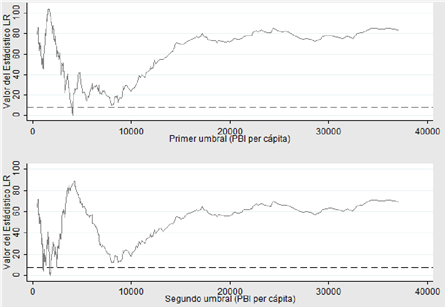
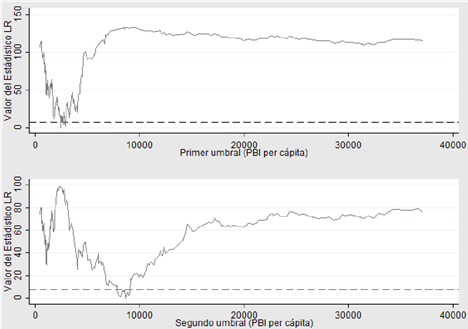
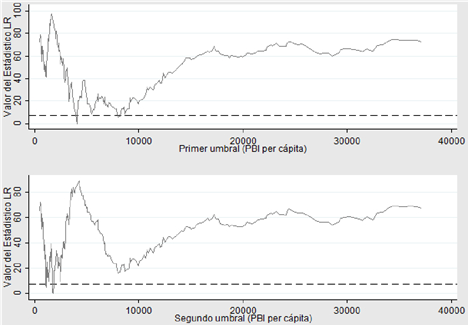
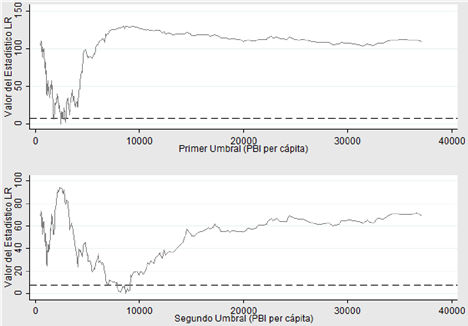
En el anexo, se incluyen las gráficas para cada uno de los modelos estimados donde se representa el proceso de determinación de los umbrales de acuerdo con la metodología descrita, así como el intervalo de confianza al 95 % para el valor estimado de los mismos, el cual se construye a partir de estadísticos likelihood ratios (LR) empleando el método de región de no rechazo. Es decir, se analiza el valor del indicador LR para los diferentes valores de la variable que consideramos umbral y establecemos valores críticos de confianza del 95 %. Si el valor estadístico cae por debajo del valor crítico (incorporado en las gráficas en líneas punteadas) se estaría determinando un valor de corte, es decir, un umbral para la variable bajo consideración, en nuestro caso el PBI per cápita.
De las variables consideradas en la especificación lineal existen tres cuyo efecto es claramente significativo sobre el crecimiento económico: la inversión (efecto positivo), el gasto público (efecto negativo) y el PBI inicial (efecto negativo). Por su parte, los coeficientes que acompañan a las variables grado de apertura y crecimiento poblacional no resultan significativos.
Con relación a los resultados encontrados para el caso de las variables inversión y PBI inicial, los mismos están en línea con la mayoría de la literatura empírica del crecimiento (Levine y Renelt, 1992; Barro, 1996; Barro y Sala-i-Martin, 2004; Durlauf et al., 2005; Delgado et al., 2014; Johnson y Papageorgiou, 2020). Con relación al PBI inicial, el coeficiente negativo justifica el efecto inercial del PBI sobre la desaceleración de la tasa de crecimiento hacia su nivel de equilibrio de largo plazo; es decir, es evidencia a favor de la existencia de un proceso de convergencia condicional.
Con referencia a la variable gasto público, el resultado obtenido de un efecto negativo sobre el crecimiento económico es compatible con lo observado por Rojas et al. (2019). Si bien otros trabajos han señalado que el gasto público guarda una relación positiva con el crecimiento (por ejemplo, Abiad, Furceri y Topalova, 2015; Fournier, 2016), estos estudios aproximan el gasto público mediante el componente de inversión pública, mientras que aquí se consideró el gasto público a partir de la partida de consumo público. Al respecto, Bose, Haque y Osborn (2007), Gemmell, Kneller y Sanz (2011) y Auerbach y Gorodnichenko (2013) establecen que el gasto del gobierno posee efectos ambiguos en función del tipo de erogación considerada. El punto crucial que justificaría la relación negativa señalada es el alto componente de gasto no productivo que se incorpora en la variable consumo público.
Con relación a las variables representativas del capital humano, se encuentra que el estatus de salud posee un efecto positivo y significativo sobre el crecimiento del PBI per cápita para todo el espacio muestral, lo cual confirma un efecto relativamente estable (al menos, siempre positivo) de la salud sobre el crecimiento en diferentes estadios del desarrollo.
La educación, sin embargo, es el componente que demuestra un comportamiento heterogéneo para economías con diferente nivel de ingreso. Los indicadores de escolarización se muestran como significativos, pero con signo negativo para el primer tramo de la distribución de ingresos en dos de las cuatro regresiones presentadas en la Tabla 3. Asimismo, los coeficientes que acompañan a las variables de educación no son significativos para valores intermedios de ingresos (valores entre umbrales señalados por el tramo T2) en todas las regresiones estimadas. Pero es interesante ver que la educación muestra un efecto positivo y significativo sobre el crecimiento a partir de niveles de ingreso por encima del segundo umbral (esto es, para el tramo T3 de la estimación).
Por tanto, estos resultados indicarían que, mientras que el estatus de salud guarda siempre una relación positiva con el crecimiento (aunque la magnitud del efecto varíe), la educación guarda una relación positiva solamente a partir de un cierto nivel de ingreso mínimo, determinado por el segundo umbral detectado. De este modo, se confirma la existencia de una relación no lineal entre la educación y el crecimiento económico. Estos resultados son compatibles con los encontrados por Mamuneas et al. (2006), Maasoumi et al. (2007) y Rojas et al. (2019). Por otra parte, los resultados obtenidos son robustos para las diferentes combinaciones de las variables de capital humano utilizadas. En efecto, la significatividad y los signos de dichas variables se mantienen en las diferentes especificaciones, lo que demuestra la robustez del análisis.
Los resultados son intuitivamente aceptables. Una población más saludable asegura una mayor productividad y, luego, un mayor crecimiento del producto independientemente del nivel de desarrollo. En cambio, un mayor nivel de educación medido a partir de años totales de escolarización tendría efectos diversos sobre el desempeño económico en función de en qué estadio de desarrollo se encuentre el país. El sustento teórico que avala este hallazgo es el postulado de existencia de no linealidades en el proceso de desarrollo económico establecido por Azariadis y Drazen (1990), lo cual origina regímenes múltiples en la relación educación-crecimiento.
En economías de bajos ingresos, la adopción de tecnología e inversión en capital se encuentra restringida, por lo que se esperan bajos retornos sobre la inversión en educación al poder combinarla en el proceso productivo con un stock de capital físico reducido, generándose un problema de auto-reforzamiento (Acemoglu, 1997; Azariadis y Stachurski, 2005; Bowles, Durlauf y Hoff, 2016). Adicionalmente, Pritchett (1999) y Kalaitzidakis et al. (2001) sugieren que en países de bajo nivel de ingreso las inversiones en educación secundaria o superior irán dirigidas hacia actividades improductivas.
La educación en estos países funciona más bien como un medio de señalización para acceder a posiciones de poder que posibilitan la extracción de rentas, antes que para incrementar la productividad de toda la economía. A su vez, significan una ineficiente asignación de recursos en situaciones donde es necesaria la inversión en actividades productivas que puedan satisfacer necesidades más básicas como la alimentación y la salud de la población. Por lo tanto, puede justificarse una relación negativa entre educación y crecimiento económico a bajos niveles de renta per cápita.
Por el contrario, en economías de ingresos altos los sectores más avanzados que incorporan capital y tecnología de punta poseen una mayor participación en el producto total. Estos sectores muestran indivisibilidades, tales como la necesidad de cubrir grandes inversiones en educación y formación para facilitar la adopción de nuevas tecnologías (Azariadis y Stachurski, 2005). A partir de un nivel mínimo de ingreso per cápita (compatible con un stock mínimo de capital per cápita) podrán potenciarse las externalidades productivas generadas por la combinación de altos niveles de capital físico y humano, cuya complementariedad en el proceso productivo ha sido notada por diversos autores (Griliches, 1969; Bartel y Lichtenberg, 1987; Vandenbussche, Aghion y Meghirl, 2006; Rojas, 2012). Por lo tanto, solamente una vez alcanzada la escala suficiente, la educación favorecerá el crecimiento económico. Esto no es posible en los países más pobres, sino en aquellos que han alcanzado un estadio mínimo de desarrollo.
Dependiendo de la especificación del modelo, el umbral inferior toma valores entre 1800 y 2400 dólares per cápita, mientras que el siguiente umbral se encuentra entre los 4000 y 8500 dólares per cápita. El hecho de que estos valores sean sensibles a la variable de educación seleccionada se debe a que es la educación la variable que presenta no linealidades fuertes. Por último, que el valor umbral sea mayor para el caso de la variable años totales de educación implica que se necesita un grado de desarrollo más elevado para aprovechar los beneficios de la educación superior en términos de crecimiento económico. La idea es que la variable medida a través el total de años de educación incluye a la población de formación superior, la cual solamente puede ser combinada con mayores niveles de capital físico en los países que han alcanzado mayores niveles de ingreso.
Conclusiones
En el presente trabajo se estudiaron los efectos de los niveles de salud y educación sobre el crecimiento económico. A partir de un modelo de regresión con umbrales para datos de panel con efectos fijos se procedió a corroborar la existencia de umbrales de ingreso y sus posibles valores. El análisis de los resultados permitió establecer la existencia de dos puntos de inflexión en la relación capital humano-crecimiento económico. Estos umbrales son especialmente sensibles a la variable de educación seleccionada, la cual muestra la mayor heterogeneidad en cuanto a su comportamiento que la variable referida a salud.
Los resultados encontrados coinciden con hallazgos previos que mencionan el efecto positivo de la educación sobre el crecimiento económico para el caso de países con ingresos per cápita inicialmente altos (Durlauf y Johnson, 1995; Pritchett, 1999; Maasoumi et al., 2007; Rojas et al., 2019) y la no significatividad de la educación para explicar el desempeño macroeconómico de países de ingresos medios (Durlauf y Johnson, 1995; Pritchett, 1999; Mamuneas et al., 2006; Maasoumi et al., 2007).
La relación positiva con el crecimiento a mayores niveles de ingreso se relacionaría con la posibilidad de adoptar nuevas tecnologías e incrementar la productividad debido a las externalidades positivas que genera un mayor nivel educativo en combinación con un alto stock de capital físico. Como mencionaron Mamuneas et al. (2006), esas externalidades estarían aún ausentes a niveles medios de renta, donde los rendimientos privados de la inversión en educación superan a los rendimientos sociales, lo que se refleja en una falta de correlación entre educación y crecimiento para los regímenes de ingresos medios.
Asimismo, la conclusión de una relación negativa entre educación y crecimiento para el caso de países de renta baja puede explicarse a partir de la existencia de bajos retornos sobre la inversión en educación y la no canalización de dichos esfuerzos a incrementar la productividad. Este resultado es coincidente con lo evidenciado por Kalaitzidakis et al. (2001) y Masanjala y Papageorgiu (2004) para los países de menor nivel de desarrollo.
Por su parte, el comportamiento de la variable salud presenta una mayor regularidad en cuanto a signo esperado y significatividad. La intuición sería que una mano de obra más saludable implica siempre una mayor productividad, favoreciendo el crecimiento independientemente del nivel de desarrollo, mientras que la educación tendría un efecto favorable sobre el desempeño de la economía a partir de un nivel mínimo de ingreso. Un corolario de recomendación de política económica es que en países de menores ingresos resultaría prioritario garantizar un nivel mínimo de salud y, a partir de allí, aplicar políticas que favorezcan el incremento en los niveles educativos.
Una posible extensión de este trabajo sería determinar a través de qué canales la educación influye sobre el crecimiento, generando relaciones adversas a bajos niveles de ingreso y retroalimentaciones positivas a mayores niveles de desarrollo. Sería interesante obtener evidencia desagregada a nivel sectorial, en particular la industria y los servicios, con el objeto de analizar en cuáles de estas actividades la educación de diferentes niveles es especialmente impulsora del crecimiento. Los resultados obtenidos facilitarían establecer recomendaciones de política educativa a fin de orientar la asignación de recursos en aquellas ramas en donde el conocimiento sea particularmente productivo, lo que favorecería el desarrollo.