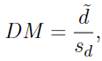Introducción
La globalización ha hecho que viajar sea una actividad cada vez más común. Mientras que en 1985 el 75 % de la población mundial necesitaba una visa para viajar a destinos extranjeros, para 2018 este porcentaje se había reducido a 53 %. De esta mayor frecuencia de viajes, los de turismo representaban el 50 % en el año 2000, y ya para el año 2018 esta participación había subido al 56 % (UNWTO, 2019).
Es ampliamente aceptado que el desarrollo del turismo conduce a mayor crecimiento económico, aunque en la literatura académica se encuentran diferencias empíricas con respecto a los canales de transmisión (Adnan & Ali, 2013; Kadir & Karim, 2012; Katircioglu, 2009). Los gobiernos, en particular los de países en desarrollo, apoyan y promueven el turismo debido a su alto efecto multiplicador en términos de generación de empleo, aumento de los beneficios en tasa de cambio, efecto positivo sobre la balanza de pagos, y estímulo de la oferta en los sectores relacionados con esta actividad (Kessy et al., 2018).
El turismo también impacta el desarrollo de la comunidad a través de la reducción de la pobreza que se da producto del mayor crecimiento económico (Croes & Vanegas, 2008; Croes & Rivera, 2018). De hecho, los numerales 8 y 10 de los Objetivos de Desarrollo Sostenible (ODS) abordan directamente el papel del turismo como una fuente de crecimiento económico sostenible (UNWTO & UNDP, 2017).
Para aquellos países receptores, estos flujos de turismo han significado que este sector sea un generador importante de ingresos y empleos, contribuyendo de manera importante al crecimiento económico. Colombia no es ajena a esta realidad y, de acuerdo con el Departamento Nacional de Estadísticas (DANE, 2020), entre 2010 y 2019 el turismo (medido desde la rama de hoteles y restaurantes) creció en promedio al 3,67 % anual y contribuyó al crecimiento del PIB total en 11,86 %. El Banco Mundial estima que los ingresos del turismo internacional representaron en 2018 el 12,23 % de las exportaciones totales (World Bank, 2020).
Por esta razón, el país ha aumentado sus inversiones en la industria turística, incluyendo campañas y estrategias que resaltan el atractivo de Colombia como destino turístico. Para que la industria turística pueda mantener una oferta continua de productos y servicios que satisfagan el creciente flujo de turistas se hace necesario contar con proyecciones sobre la demanda futura de turistas al país.
Un elemento crucial en la proyección de la demanda turistas es la información oportuna. No obstante, en el mejor de los casos, la mayoría de los datos sobre turismo se publican con un rezago de dos meses. De igual forma, dado que la información extrae de los participantes de la industria, el acceso a la misma se vuelve costoso y dispendioso. Tener información en tiempo real sobre la demanda de turistas puede ayudar a mejorar aspectos claves tales como la asignación de presupuesto de mercadeo al permitir estimar el comportamiento futuro de viajeros de mercados entrantes al mercado de destino.
Tanto para la industria turística como para los encargados de la política pública del sector, es crucial tener la información más actualizada posible sobre la demanda de turistas. Esta necesidad de “pronosticar el presente”-o nowcasting como se conoce en la literatura económica- ha llevado a incorporar en los modelos estadísticos variables que estén disponibles lo más pronto posible, siendo en su mayoría de casos encuestas cualitativas de tendencias sobre el sector. Sin embargo, debido al sesgo evidente que se presenta en la medición de variables de este tipo, es necesario buscar fuentes alternativas de información que se produzcan en tiempo real.
Diversos estudios han mostrado que la información producida por motores de búsqueda -en especial la de Google Trends- mejora los pronósticos de modelos tradicionales, al incorporar en los mismos información útil y diversa. En particular, el creciente uso del internet hace que cada vez más personas “revelen” su intención de visitar un destino a través de sus búsquedas en la web. En este sentido, los datos que producen los criterios de búsqueda sobre destinos turísticos podrían estar altamente correlacionados con la llegada de turistas al país y, por lo tanto, ser usados como un indicador en tiempo real de la demanda de turismo por la industria y los encargados de la política pública.
A través de este estudio se indaga si los datos producidos por el criterio de búsqueda “Colombia” en la categoría “travel” en Google Trends permiten mejorar la precisión de pronóstico de la de la demanda de turistas con respecto a un modelo base. En particular, se asume que las personas realicen búsquedas previas sobre sus destinos turísticos en internet mientras planean sus vacaciones y dado que Google Trends presenta información sobre el interés relativo de diferentes términos de búsqueda, esto se puede interpretar como un indicador de viaje hacia el destino turístico.
Para este fin propuesto en este artículo, se analiza el grado en que las series de tiempo generadas en Google Trends mejoran la capacidad de predicción de un modelo simple que utiliza como predictor los rezagos propios de la llegada de turistas en comparación con dos especificaciones alternativas: (i) el modelo base aumentado con la inclusión de datos mensuales de Google Trends) ; y (ii) el modelo base, pero modificado con la inclusión de datos semanales de Google Trends.
Para los próximos años se espera que el sector del turismo sea el motor de la economía colombiana y -dada la poca literatura sobre proyección de flujos de turismo que existe para el caso de Colombia- este artículo pretende ser una contribución importante al desarrollo de métodos cuantitativos de predicción que puedan ser usados por esta industria y las autoridades encargadas de la política de turismo en el diseño y planeación de programas que permitan que Colombia se consolide como uno de los principales destinos turísticos de la región.
Este artículo está organizado de la siguiente manera: en esta introducción se discuten el problema y objetivo de investigación; en la primera sección se revisan los estudios más relevantes relacionados con la predicción de la demanda de turistas; la segunda presenta los datos a utilizar, las transformaciones realizadas a los mismos, y la metodología a emplear; la sección tres discute los resultados; finalmente, se presentan las conclusiones más relevantes y las principales implicaciones para la industria turística y para los encargados de la política pública de turismo.
I. Revisión de literatura
Los estudios sobre proyección de flujos de turismo emplean métodos cuantitativos causales y no causales con el propósito de caracterizar y analizar el comportamiento de los turistas, identificar variables relevantes que incidan en la demanda de turistas al igual que patrones estacionales y de tendencia (Guizzardi & Mazzocchi, 2010). Gonzáles y Moral (1995) usan índices de precios de los países de origen y destino para evaluar el poder predictivo que las preferencias de los turistas tienen en la elección de España como destino turístico. Song et al. (2011) estudian los flujos de turismo hacia Hong Kong provenientes de China, Corea del Sur, Reino Unido, y los Estados Unidos usando índices de precios y diferentes de métodos de series de tiempo.
Claveria y Torra (2014) comparan el poder predictivo de diferentes métodos de series de tiempo y encuentran que modelos del tipo ARIMA (Autoregresive Integrated Moving Avergae) presentan un mejor desempeño que métodos más sofisticados como SETAR (Self Exciting Threshold Autoregressive) y ANN (Artificial Neural Network). Valencia et al. (2017) comparan la capacidad de predecir la llegada de turistas a Medellín (Colombia) de modelos de regresión clásica y modelos bayesianos, encontrando que los segundos presentan una mayor capacidad de predicción que los primeros.
La última década se ha caracterizado por un aumento sin precedentes en la cantidad de información, recursos, servicios, y datos, a los cuales se puede acceder a través de internet. Este crecimiento en información y datos se denomina como big data y ha implicado una transformación social profunda por las diferentes aplicaciones que se le da a este mayor volumen de información. De acuerdo con Khoury e Ioannidis (2014), big data es aquella información interconectada, constituida por altos volúmenes de datos que presentan estructuras complejas. Como ejemplos representativos de big data es posible mencionar datos de redes sociales, registros de llamadas, datos de sitios web de carácter comercial, información geográfica, datos sobre trayectorias de vehículos, y datos de motores de búsqueda.
Entre la información producida en sitios web se destaca la de Google Trends, herramienta producida por Google, y la cual analiza la popularidad de las consultas de búsqueda realizadas en el motor de búsqueda en diferentes regiones e idiomas. Desde su lanzamiento en 2006, Google Trends ha atraído el interés tanto de la industria como de la academia como instrumento para predecir diferentes fenómenos. Es posible encontrar aplicaciones en epidemiología (Wilson & Brownstein, 2009; Ginsberg et al., 2009), sector automotor (Carriere-Swallow & Labbé, 2013), desempleo (Askitas & Zimmerman, 2009), comportamiento del consumidor (Silva et al., 2019).
En el área de turismo, los datos de Google Trends han sido utilizados por diferentes autores tales como Rivera (2016) quien encuentra que existe una correlación alta entre las búsquedas en Google y el número de visitantes en los hoteles de Puerto Rico. De igual forma, Yang et al (2015) comparan el poder de Google Trends y Baidu en la proyección de visitantes a China y como principal resultado encuentran que Baidu tiene un mejor desempeño que Google Trends ya que Baidu es más popular en China que Google.
Önder (2017) utiliza Google Trends para proyectar la demanda de turismo en dos ciudades (Viena y Barcelona) y dos países (Austria y Bélgica), pero con la novedad que no solo utiliza criterios de búsqueda sino también búsqueda de imágenes de los destinos estudiados. En general, este autor encuentra que la calidad de las proyecciones para Viena aumenta con la inclusión de imágenes y en menor medida para los otros tres destinos.
Finalmente, Bangwayo-Skeete y Skeete (2015) y Havranek y Zeynalov (2021) examinan la utilidad de Google Trends para proyectar los flujos de turismo hacia cinco destinos del Caribe y a la ciudad de Praga (República Checa), respectivamente. Estos autores sugieren que incluir datos semanales de Google Trends mejora la capacidad explicativa y predictora con relación a modelos simples autorregresivos.
II. Modelo econométrico
A. Datos
De acuerdo con el portal StatCounter (2020), el motor de búsqueda de Google cuenta con una participación de mercado del 92,71 % a nivel mundial, seguido por Bing (2,73 %) y Yahoo (1,47 %). De hecho, “googlear” se ha vuelto un verbo común cuando las personas se refieren a buscar algo en internet, lo que evidencia la importancia de Google como motor de búsqueda de cualquier tipo información. Dado que el turismo es una industria intensiva en información, Google contiene una cantidad de información relacionada con este sector. De manera específica, la herramienta Google Trends, permite analizar la popularidad que han tenido diferentes criterios de búsqueda a través del tiempo.
Los datos de Google Trends siempre son relativos ya que son índices del volumen de criterio de búsqueda (por ejemplo, “Colombia”) en un área geográfica dada (por ejemplo, “worldwide”) y, de manera opcional, para una categoría de interés (por ejemplo, “travel”). Los índices se construyen tomando el porcentaje de consultas -es decir, el número de consultas para “Colombia” en proporción a todas las demás consultas en el área geográfica especificada en la categoría de interés (si se especificó)- y el volumen diario más alto durante un periodo determinado de tiempo es normalizado a 100 (Choi & Varian, 2012).
Las consultas de búsqueda incluyen descripciones cortas o breves de los términos que están relacionados a las necesidades individuales del individuo tal como “vuelos a Colombia”. Una persona puede usar diversos criterios para obtener la información deseada del motor de búsqueda, no obstante, Google Trends agrupa todos los criterios de búsqueda relacionados con viajes en la categoría “travel”, incluyendo atracciones, hospedaje, transporte, entre otros (Google Trends, 2020). En ese sentido, al usar Google Trends se pueden obtener datos que capturan el criterio de búsqueda usado en este estudio (“Colombia”) en la categoría “travel”.
Las series sobre llegada mensual de turistas procedentes de diferentes partes del mundo para el período comprendido entre abril del 2011 y junio del 2019 se obtuvieron de los sitios web Centro de Información Turística de Colombia (CITUR) al igual que del sitio web de Migración Colombia. Las llegadas de turistas corresponden a las hechas por vía área para tener concordancia con los criterios utilizados en la obtención de las series de Google Trends1.
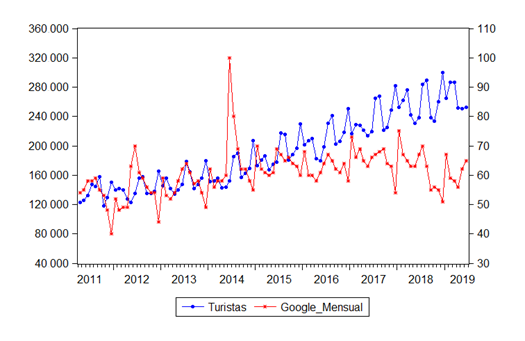
La Figura 1 compara la llegada mensual de turistas con el índice de intensidad de búsqueda mensual de Google Trends mensual. Las dos variables presentan una correlación fuerte con tendencia creciente, lo que indica que tanto el atractivo de Colombia como destino turístico al igual que el interés de las personas de otros países por viajar a Colombia han ido aumentando con el tiempo. Adicionalmente, las series exhiben patrones estacionales, algo común en los datos de turismo. La Figura 2 compara la llegada mensual de turistas con el índice de intensidad de búsqueda semanal de Google Trends mensual exhibiendo los mismos patrones que para los datos mensuales.
Para garantizar relaciones funcionales de carácter lineal entre las variables de estudio, los datos correspondientes a llegada mensual de turistas y los índices de Google Trends son transformados a logaritmos naturales. De igual forma, los datos son ajustados estacionalmente usando una descomposición del tipo STL2. De esta manera, las diferentes proyecciones de la llegada de turistas se pueden ajustar por su componente estacional para poder compararlas con los datos originales de llegada de turistas3
Figura 1
Llegada mensual de turistas a Colombia e intensidad de búsqueda mensual del criterio “Colombia” en la categoría “Travel” de Google Trends
Fuente: elaboración propia con datos de Google Trends y CITUR (2020).
Figura 2
Llegada mensual de turistas a Colombia e intensidad de búsqueda semanal del criterio “Colombia” en la categoría “Travel” de Google Trends
Fuente: elaboración propia con datos de Google Trends y CITUR (2020).
La Tabla 1 presenta los resultados de tres pruebas diferentes utilizadas para determinar la existencia de raíces unitarias en las diferentes series. Los resultados de las pruebas indican que se rechaza la existencia de una raíz unitaria para el logaritmo natural de la llegada de turistas cuando se incluye constante y tendencia. De igual forma, se rechazar la hipótesis nula de una raíz unitaria para el logaritmo natural de los datos mensuales y semanales de Google Trends.
Tabla 1
Pruebas de raíz unitaria
B. Metodología
Para determinar la utilidad de Google Trends como predictor de la llegada mensual de turistas a Colombia, se parte de un modelo base el cual se compara con dos modelos alternativos que usan información de Google Trends. En el primer modelo alternativo esta información es mensual, en tanto que en el segundo esta información es semanal.
El modelo base asume que es posible predecir la llegada mensual de turistas a partir de sus propios rezagos. El segundo modelo de comparación establece que es posible explicar la llegada mensual de turistas utilizando no solo rezagos propios sino también los criterios de búsqueda mensual de Google Trends. Este modelo es el modelo base, pero asumiendo que la llegada de turistas depende no solo de su propio pasado (parte autorregresiva) sino de valores actuales y pasados de variables explicativas adicionales (parte de rezagos distribuidos).
La novedad de este trabajo es el tercer modelo, que aumenta el modelo base con datos de Google Trends cuya frecuencia es semanal. Los modelos de regresión estándar requieren que las regresiones tengan la misma frecuencia que la variable dependiente. Esta restricción no siempre se cumple en la práctica -en economía la mayoría de series estadísticas se producen de manera anual, trimestral, mensual e inclusive diaria-.
Por lo general, existen dos aproximaciones para estimar regresiones donde las variables dependiente e independiente exhiben frecuencias mixtas. La primera aproximación consiste en sumar o promediar los datos de alta frecuencia para que queden en la misma frecuencia que los datos de baja frecuencia. Para este fin, se incluye un coeficiente por cada variable de alta frecuencia para que de esta forma cada valor en el promedio tenga la misma ponderación.
En la segunda aproximación, los componentes individuales de los datos de alta frecuencia son incluidos en la regresión de manera tal que se tenga un coeficiente separado para cada componente de alta frecuencia. Por ejemplo, cuando se estima una regresión anual con regresores de frecuencia mensual, es posible agregar cada uno de los componentes mensuales como regresores. Esta aproximación lleva a que se tenga que estimar un número alto de coeficientes de regresión.
Debido a la pérdida de eficiencia en estimación que exhiben estas dos aproximaciones, Ghysels et al. (2006); Andreou et al. (2010); Ghysels et al. (2020), proponen una alternativa en la cual se permite que la variable dependiente en la regresión tenga una frecuencia menor a las variables explicativas. Esta alternativa es conocida en la literatura de series de tiempo como MIDAS (Mixed Data Sampling) y permite de manera simple y flexible usar datos de alta frecuencia para explicar datos de baja frecuencia.
El método MIDAS es el punto medio de las dos aproximaciones mencionadas anteriormente, ya que permite funciones diferentes de ponderación simultáneamente reduciendo el número de coeficientes a estimar. De esta manera, MIDAS ofrece una aproximación a la estimación de frecuencias mixtas caracterizada por la flexibilidad y una parametrización simple y flexible de la respuesta de la variable dependiente de baja frecuencia a cambios en la variable independiente de alta frecuencia.
Específicamente, el modelo bajo consideración es:
donde Yt es la variable dependiente de baja frecuencia,
 un regresor (regresores) de alta frecuencia con S valores para cada valor de baja frecuencia, f es una función que describe el efecto de la variable de alta frecuencia sobre la
variable dependiente de baja frecuencia, y θ,λ son parámetros para estimar.
un regresor (regresores) de alta frecuencia con S valores para cada valor de baja frecuencia, f es una función que describe el efecto de la variable de alta frecuencia sobre la
variable dependiente de baja frecuencia, y θ,λ son parámetros para estimar.
El método de estimación MIDAS ofrece diferentes funciones de ponderación que se ubican en un punto medio entre las aproximaciones de coeficientes individuales y la agregación con ponderaciones iguales. El uso de funciones de ponderación en el método MIDAS permite que se reduzca el número de parámetros en el modelo ya que estas funciones fijan restricciones sobre los efectos rezagados de la variable de alta frecuencia. La parametrización de la función de ponderación puede tomar diferentes formas funcionales para mantener la flexibilidad y parsimonia del modelo. No obstante, las especificaciones más utilizadas en trabajo empírico son las ponderaciones Almon y Beta.
La ponderación Almon es una extensión del polinomio de rezagos distribuidos (Almon, 1965) que fija restricciones sobre los coeficientes de los rezagos en modelos autorregresivos, lo que a su vez la convierte en candidato natural para la ponderación de frecuencias mixtas. Por cada rezago de alta frecuencia hasta k, los coeficientes de la regresión se estiman utilizando rezagos polinomiales de dimensión p en los parámetros θ de la regresión MIDAS. En este caso, el modelo de regresión es:
donde p es el orden del polinomio Almon, y el número de rezagos seleccionados k pueden ser menores que o mayores que S.
Es importante señalar que el número de coeficientes a ser estimados depende del orden del polinomio y no del número de rezagos de alta frecuencia. Esto puede ser visto de manera más clara escribiendo (2) de la siguiente manera:
De esta manera, es más fácil ver la asociación de los coeficientes θl con cada uno de los órdenes p de la variable Zl, t.
La ponderación Beta (Ghysels et al., 2006) hace uso de la función beta normalizada. El modelo de regresión correspondiente esta dado por:
donde k es un numero de rezagos, λ es un coeficiente de pendiente que es común para todos los rezagos, y
donde δ es un número muy pequeño que en la práctica es aproximadamente igual a 2,22exp−16.
La función beta es extremadamente flexible y puede tomar diferentes formas, las cuales pueden ser creciente, decreciente, plana, jorobada, o en forma de U dependiendo de los tres parámetros AR-MIDAS (θ 1 ,θ 2 ,θ 3).
C. Modelos
Para verificar la hipótesis de que los datos de Google Trends mejoran el poder predictivo de la llegada de turistas se plantean los siguientes modelos:
Un modelo base con valores rezagados de llegada de turistas y una tendencia determinística lineal como las únicas variables explicativas
Un modelo alternativo I que incluye valores rezagados de la llegada de turistas al igual que valores contemporáneos y rezagados de los criterios de búsqueda Google Trends mensuales más una tendencia determinística lineal (denominado GTM).
Un modelo alternativo II que incluye valores rezagados de la llegada de turistas y valores contemporáneos y rezagados de los criterios de búsqueda Google Trends semanales más una tendencia determinística lineal (denominado GTS).
La variable dependiente ln (llegadas t) es una variable de baja frecuencia y representa el logaritmo natural desestacionalizado de la llegada mensual de turistas. ln (googlem t) es el logaritmo natural desestacionalizado de la intensidad de búsqueda mensual del criterio “Colombia” en la categoría “Travel” de Google Trends. ln (googlew t) es una variable de alta frecuencia y equivale al logaritmo natural desestacionalizado de la intensidad de búsqueda semanal del criterio. “Colombia” en la categoría “Travel” de Google Trends. La función B (k; θ) es una especificación polinomial que determina las ponderaciones para agregación temporal tales como Beta o Almon. Li es el operador de rezagos de la variable dependiente llegadas t , y L k/w representa el operador de rezagos para la variable independiente de alta frecuencia googlew t
Dado que la variable dependiente está en logaritmo, βi representa la elasticidad de los valores rezagados de llegadas
t, γi es la elasticidad de googlem
t sobre llegadas
t, δ es la elasticidad de la variable de alta frecuencia googlew
t sobre llegadast Finalmente, α es una constante, ϑ el efecto del tiempo sobre la tasa de crecimiento mensual de llegadast, y ϵt y ϵ
w
t
son errores independiente e idénticamente distribuidos
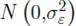 .
.
III. Discusión de resultados
Los resultados de los modelos base, Google Trends mensual, y dos especificaciones de Google Trends semanal, se presentan en la Tabla 2. Todos los modelos exhiben R2’s altos con coeficientes individuales significativos. La tendencia desempeña un papel importante en explicar la llegada de turistas para todos los modelos.4
El modelo base muestra que aumentos en la llegada de turistas de uno y cinco meses atrás ayuda a explicar estadísticamente la llegada actual de turistas. El modelo alternativo I, el cual es el modelo base aumentando por datos mensuales Google Trends, muestra que cuando el índice de búsquedas aumenta su intensidad en 10 % doce meses después se evidencia un aumento estadísticamente significativo del 10,36 % en la llegada de turistas.
El modelo alternativo II toma el modelo base y lo extiende incluyendo datos semanales de Google Trends. Este modelo se estima utilizando regresiones AR-MIDAS5 con dos especificaciones diferentes de la ponderación semanal y la llegada del mes actual se explica utilizando un rezago de 52 semanas, incluyendo la primera semana del mes a explicar. Los resultados muestran que la inclusión de los datos semanales de Google Trends se justifica dada la significancia estadística del primer rezago (los demás rezagos no se presentan).
Tabla 2
Resultados estimación modelos base y alternativos. Abril 2011 - Junio 2019
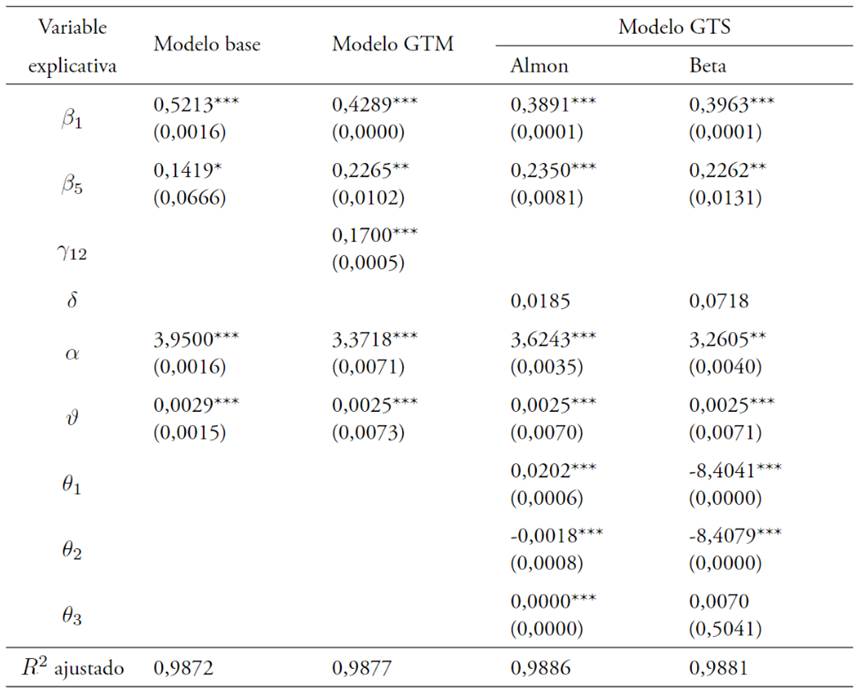
[i]Nota: ***, ** y * indican significancia a los niveles de 1 %, 5 % y 10 % respectivamente. P-valores entre paréntesis. β’s muestran los coeficientes rezagados de la llegada mensual de turistas. γ’s denotan los coeficientes de Google Trends mensual en la regresión ARDL. δ’s son los coeficientes de Google Trends semanal en las regresiones MIDAS. α es la constante en las diferentes regresiones. ϑ es la tendencia en las diferentes regresiones. θ’s son hiperparametros que determinan la forma de la función de ponderación en las regresiones MIDAS.
Estos resultados son consistentes con otros estudios, tales como los de Bangwayo-Skeete y Skeete (2015), Öender (2017), y Havranek y Zeynalov (2019), en los cuales se evidencia que utilizar los datos de Google Trends produce modelos que explican la llegada de turistas con mayor bondad de ajuste y mejor capacidad de predicción que un modelo base de valores rezagados de la variable dependiente.
A. Evaluación proyecciones
Ya que el interés principal de este artículo es determinar la utilidad de Google Trends para predecir la llegada mensual de turistas, se requiere evaluar cada uno de los tres modelos estimados, no solo en términos de su bondad de ajuste en el periodo muestral sino también en el desempeño de cada uno para predecir por fuera del periodo muestral.
Para determinar qué modelo se desempeña de mejor manera en términos de capacidad predictiva se usan los estadísticos MAPE (Mean Absolute Percentage Error) y RMSE (Root Mean Squared Error). Adicionalmente, un modelo de predicción de promedio simple se usa como contraste. Las proyecciones de cada modelo se evalúan para periodos de 1, 2, 3, 6, y 12 meses. Los resultados de las evaluaciones de predicción se presentan en la Tabla 3 y en la misma se indica la clasificación de cada modelo, donde 1 indica el mejor modelo para predecir por horizonte de tiempo.
Según la información presentada en la Tabla 3, los modelos que incluyen datos semanales de Google Trends exhiben la mejor calidad de predicción para todos los horizontes excepto para un horizonte de 6 meses. También es de destacar que el modelo de pronóstico simple supera al modelo al modelo base que solo usa valores rezagados de la variable dependiente. Vale la pena anotar que en un horizonte de seis meses el modelo que usa datos mensuales de Google Trends es el mejor seguido por el modelo de promedio simple que también exhibe mejor desempeño que los modelos de Google Trends que usan datos semanales
Las ponderaciones Almon y Beta exhiben un desempeño bastante consistente (siempre en primer o segundo lugar, a excepción de seis meses), aunque el polinomio Almon es en un poco irregular (en términos de MAPE y RMSE relativo al polinomio Beta). Esto, en cierta medida, es esperado ya que el polinomio Almon es sensible a la selección del rezago. Es probable que el número óptimo de rezagos cambie dependiendo del horizonte de tiempo. Sin embargo, en este artículo se utiliza un número fijo de rezagos para todas las estimaciones y por lo tanto no es sorprendente que el desempeño del polinomio Almon cambie.
Estos resultados muestran que los modelos AR-MIDAS producen reducciones significativas en los errores medios al cuadrado para horizontes cortos de tiempo. En particular, el modelo GTS-Beta proporciona valores significativos que reducen los errores de predicción en comparación con los otros modelos. En particular, se puede observar que para todos los horizontes de tiempo (a excepción de seis meses), al menos uno de los modelos que incluyen datos semanales de Google Trends tiene mejor poder de pronóstico que los base, de promedio simple, o que usa datos mensuales de Google Trends. De hecho, se resalta que para un horizonte de tiempo de 12 meses el modelo de promedio simple se ubica según el criterio MAPE, aunque el modelo GTS-Beta quedó de segundo.
Aunque en la práctica, los indicadores tradicionales, tales como MAPE y RMSE, son ampliamente utilizados para evaluar y comparar pronósticos debido a su facilidad y comprensión, los mismos presentan limitaciones en algunos casos. Por un lado, cuando la diferencia estocástica tiene un impacto significativo en los pronósticos producidos por lo diferentes modelos, los indicadores tradicionales pueden incluso dar resultados confusos en los casos más desfavorables (Fildes, 2008). Por otra parte, como lo muestran Armstrong y Collopy (1993) estos indicadores tradicionales se ven afectados por la existencia de datos atípicos y no son independientes de la unidad de medida, a menos que estén expresados como porcentaje.
Para solventar estos problemas, se utiliza la prueba Diebold-Mariano (Diebold & Mariano, 1995) para evaluar el desempeño de cada uno de los modelos que incluyen datos de Google Trends en referencia al modelo base.
Para este fin, y teniendo que cuenta que la industria y los encargados de política planifican en horizontes de corto y mediano plazo, se selecciona un periodo de evaluación de dos años. Por lo tanto, para los tres modelos, la muestra de entrenamiento va de julio de 2011 a junio de 2017 y la muestra de proyección de julio de 2017 a junio de 2019.
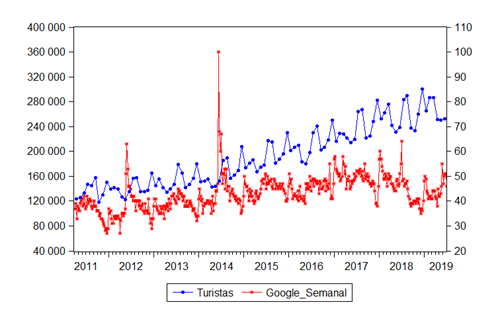
De manera formal, la prueba Diebold-Mariano (DM) compara la calidad de las predicciones generadas por un modelo alternativo con las de un modelo base utilizando el siguiente estadístico:
donde d˜ y sd representan el promedio y la deviación estándar muestral de d. Donde d = ϵ1 − ϵ2. ϵi puede ser la diferencia absoluta o cuadrada de los valores proyectados y los valores reales de los dos modelos (i = 1, 2). Bajo la hipótesis nula de esta prueba las predicciones de los dos modelos tienen la misma exactitud y bajo la hipótesis alternativa las proyecciones del modelo alternativo superan a las del modelo base.
La Tabla 4 presenta los resultados de esta prueba y para cada modelo se rechaza la hipótesis nula. Por lo tanto, es posible concluir que los modelos alternativos I y II son mejores que el modelo base y, en ese sentido, la inclusión de los datos de Google Trends puede ayudar a tener mejores predicciones sobre flujos turísticos hacia Colombia.
Es posible afirmar que índices cuidadosamente identificados sobre intensidad de búsqueda en sitios web, tales como los producidos por Google Trends, incluyen señales tempranas que pueden ayudar de manera considerable a predecir la llegada de turistas a Colombia. Los resultados presentados indican que existe una ventaja informacional en usar datos de alta frecuencia (semanales) para pronosticar una variable de baja frecuencia (mensuales) tal y como lo es la llegada de turistas al país. En ese sentido, para investigaciones futuras, se sugiere examinar si el uso de múltiples variables explicativas de alta frecuencia (diarias o semanales) pueden mejorar aún más los pronósticos de llegada de turistas.
Tabla 4
Evaluación proyecciones. Prueba Diebold-Mariano
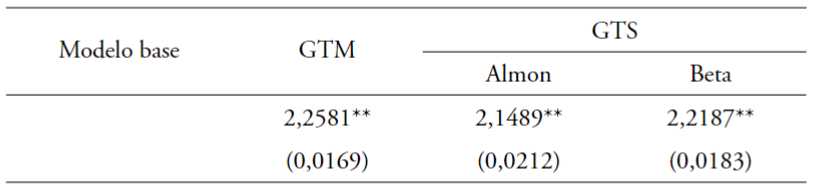
[i]Nota: Un valor positivo y significativo de la prueba DM significa que las proyecciones producidas por los modelos alternativos 1 y 2 (ARDL y AR-MIDAS) son estadísticamente superiores a las producidas por el modelo base (AR). En contraste, un valor no significativo implica que las proyecciones del modelo alternativo son estadísticamente iguales a las del modelo base. El estadístico utilizado es la diferencia cuadrada, ϵi = (yˆi − yi)2.
Conclusiones
Contar con proyecciones adecuadas sobre la demanda de turistas es importante no solo para la industria turística, sino también para la economía como un todo, dada la contribución que este sector hace al crecimiento económico de países cuyo principal motor es el turismo. Este tema cobra más valor en un entorno global donde la incertidumbre es la regla, lo que a su vez modifica el comportamiento de turistas internacionales haciendo más difícil los procesos de planeación tanto de la industria turística como de las autoridades encargadas del diseño de la política de turismo. A esto también se suma que las proyecciones en la industria del turismo por lo general se realizan usando datos provenientes de fuentes secundarias cuya disponibilidad pública se da con meses de retraso.
Los motores de búsqueda son una fuente importante para obtener datos sobre turismo y evaluar dinámicas de su consumo. De hecho, búsquedas en la categoría “Travel” de Google sobre países destino pueden indicar llegadas futuras o potenciales de turistas. Esto ha motivado que en este estudio se determine el impacto que los datos de Google Trends sobre intensidad de búsqueda del criterio “Colombia” tienen sobre la llegada de turistas al país.
Los resultados evidencian que la industria del turismo y las autoridades encargadas de la política pública de turismo se pueden beneficiar en utilizar los datos de Google Trends -como complemento a la información tradicional- para predecir la llegada de turistas en horizontes de un año y mejorar de esta manera sus procesos de planeación. Simultáneamente, otras industrias también pueden utilizar esta metodología basándose en sus propios criterios de búsqueda para predecir tendencias útiles.
No obstante, es importante anotar que usar Google Trends como la única variable para predecir no está exenta de sesgos, puesto que la motivación para buscar información en motores de búsqueda depende de factores internos y externos difíciles de determinar. ¡De igual forma, tampoco se puede asumir que todos los que buscan información sobre un destino tienen la intención de visitar ese lugar; lo que realmente indican estas búsquedas es un interés de las personas. Por lo tanto, es importante contar con información adicional que complemente los pronósticos en tiempo real que se producen utilizando Google Trends.
Por ejemplo, el criterio de búsqueda “Colombia” en la categoría “Travel” se puede mejorar si se incluyen las búsquedas en el idioma nativo del turista (por ejemplo, mandarín o ruso); también si la información de Google Trends no se limita a utilizar términos de búsqueda, sino que se expande para incluir imágenes sobre los destinos turísticos de interés. Así, se pueden asignar recursos de manera mucho más eficiente y reducir costos.
Poder reaccionar de manera adecuada y rápida a picos previsibles de corto plazo de llegada de turistas de ciertos mercados permitiría -por ejemplo- que haya suficientes folletos en chino, un número adecuado de guías turísticos que hablen italiano, o los buses necesarios para el traslado de turistas del aeropuerto a los hoteles respectivos. De igual forma, a diferencia de muchos de los datos que tradicionalmente se utilizan para pronosticar la llegada de turistas, los datos de Google Trends están disponibles de manera gratuita y oportuna (semanales) y con el uso de los modelos adecuados, pueden ser fácilmente incorporados por la industria.
Es importante señalar que, incluso si los datos de Google Trends indican intención de visitar, puede existir un sesgo de selección con Google Trends ya que esta herramienta no recoge información de otros grupos demográficos que no usan esta herramienta y que pueden ser bastante heterogéneos en términos de edad, ingreso, y nivel educativo. Adicionalmente, en el mercado también existen un variado número de aplicaciones que ofrecen información y recomiendan diferentes sitios turísticos que eventualmente pueden limitar el uso de motores de búsqueda para buscar información sobre destinos turísticos. En ese sentido, se podrían utilizar algoritmos de machine learning y data mining que permitiesen recopilar información demográfica de los potenciales turistas para complementar los datos de Google Trends.
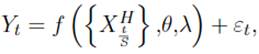
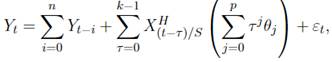
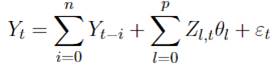
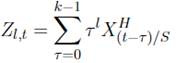
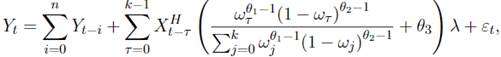
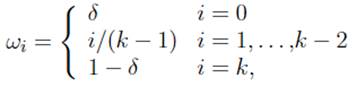
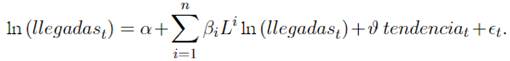 (4a)
(4a)
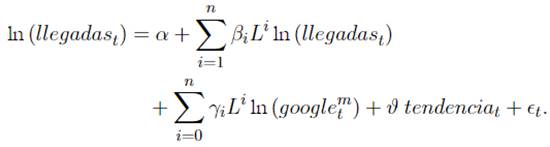 (4b)
(4b)
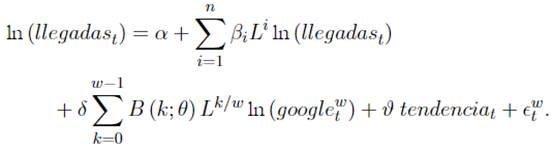 (4c)
(4c)