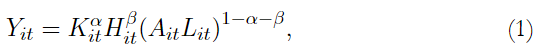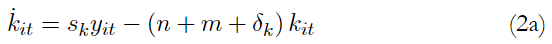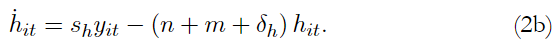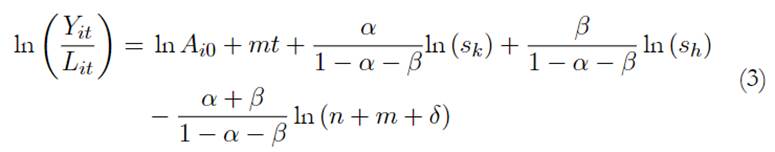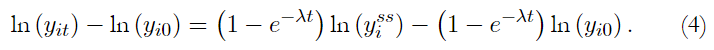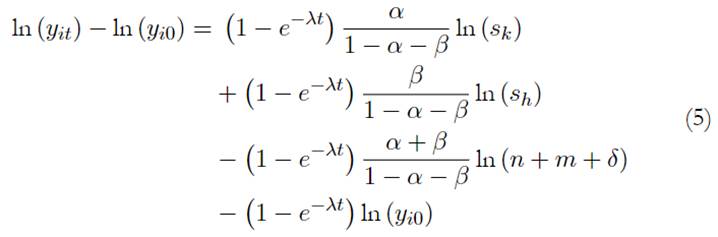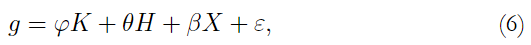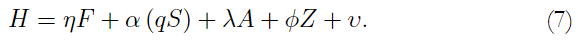Introducción
El capital humano es uno de los determinantes más importantes de los ingresos y el crecimiento económico. Shultz (1961), uno de los primeros en teorizar sobre el capital humano, creía que las actividades que pueden mejorar en gran medida las capacidades humanas están relacionadas con instalaciones y servicios de salud, experiencia y capacitación en el trabajo, y la educación formal. Sin embargo, desde finales del siglo pasado ha venido ganando importancia el componente de educación como representación del capital humano. Es así como en las últimas tres décadas se ha publicado una amplia cantidad de estudios empíricos que indagan acerca de la relación entre el capital humano y la tasa de crecimiento económico entre países, empleando como proxies, primero, información sobre la tasa de matriculación escolar, luego, datos sobre los años de escolaridad alcanzados por la población en edad de trabajar, y más recientemente, las habilidades cognitivas de la población trabajadora.
El objetivo de este artículo es probar en el contexto de los departamentos colombianos el efecto que ha sido estimado en estudios a nivel internacional, empleando muestras amplias de países, de las habilidades cognitivas sobre el crecimiento económico. Sin embargo, el análisis va más allá al contrastar la heterogeneidad de dichos efectos dependiendo de: a) las diferentes áreas del conocimiento evaluadas en las pruebas Saber 11 que se incluyan en las regresiones, b) diferentes agrupaciones de departamentos basadas en niveles de PIB per cápita, tasa de crecimiento del PIB por habitante y tamaño de sus economías, y c) diferentes periodos de tiempo.
El artículo se divide en cuatro secciones. A continuación, se presenta una revisión de la literatura con las más importantes referencias a nivel mundial sobre la relación entre habilidades cognitivas y crecimiento. En la sección II se presentan los modelos teórico y empírico que guían el trabajo a desarrollar con los datos. El tercer apartado muestra los resultados obtenidos en las distintas estimaciones, y finalmente, se cierra con las principales conclusiones e implicaciones de política.
I. Educación, capital humano y crecimiento económico
En los años sesenta del siglo pasado empezó a documentarse el potencial de la formación de capital humano con trabajos como los de Shultz (1961), Becker (1962), y Nelson y Phelps (1966), entre otros1. Así, el capital humano en forma de educación ha sido tratado desde diversas perspectivas: como factor de producción por Mankiw et al. (1992); como potenciador de la capacidad de innovación de la fuerza laboral por Romer (1990) y Aghion y Howitt (1998); o como facilitador de la difusión del conocimiento en la adopción de nuevas tecnologías por Benhabib y Spiegel (2005).
La mayoría de la literatura sobre el crecimiento económico ha empleado los años de escolaridad de la fuerza laboral como factor determinante y como una variable proxy del capital humano. Sin embargo, los primeros estudios utilizaron diferentes aproximaciones para el capital humano de una economía: por ejemplo, tasas de alfabetización de adultos (Azariadis & Drazen 1990; Romer 1990) o matriculación escolar (Barro 1991; Mankiw et al. 1992; Levine & Renelt 1992). Una posterior evolución se centró en considerar los años de escolaridad (Cohen & Soto 2007; Krueger & Lindahl 2001), entre otros. En la actualidad este concepto ha evolucionado. Ha venido ganando protagonismo el concepto de capital humano como el resultado del proceso de lo que los estudiantes saben y pueden hacer, medido habitualmente con los puntajes obtenidos en pruebas estandarizadas (Hanushek & Kimko, 2000; Hanushek & Woessmann, 2008, 2012a, 2012b).
Los trabajos pioneros hicieron amplio uso de los años de escolaridad como factor determinante de mayores tasas de crecimiento económico. Los estudios de Easterlin (1981), Laing et al. (1995), y Behrman et al. (1999) dan cuenta de ello. No obstante, el nuevo siglo vino con una nueva forma de tratar y medir la educación como factor determinante del crecimiento económico. Uno de los primeros y -quizá- más importantes estudios en emplear las habilidades cognitivas de las personas como variable representativa de la educación fue el de Hanushek & Kimko (2000). A través de la utilización de los puntajes en pruebas internacionales administradas por la International Association for the Evaluation of Educational Achievement (IEA) y la International Assessment of Educational Progress (IAEP), para una muestra de 31 países entre 1960 y 1990, encontraron una fuerte relación positiva entre habilidades cognitivas y crecimiento económico.
Los datos del puntaje promedio en las pruebas empleados por Hanushek & Woessmann (2008, 2012a, 2012b) fueron de estudiantes entre 9 y 15 años de edad, obtenidos entre 1964 y 2003 para países desarrollados, y entre 1990 y 2003 para países en desarrollo, los cuales se usaron para su análisis del periodo 1960-2000. Por su parte, Breton (2011, 2015) empleó datos similares, pero esta vez para analizar los años entre 1985 y 2005 en países desarrollados y en vías de desarrollo. En el caso de Altinok y Aydemir (2017), hicieron uso de las mismas fuentes de datos, pero para un grupo de países más grande y periodo de tiempo mayor, 1960-2012. En todos los casos anteriores se estimaron modelos de corte transversal, lo cual es superado en este artículo por las estimaciones de datos panel.
II. Un modelo de crecimiento con habilidades cognitivas
América Latina es un interesante caso, donde un logro escolar relativamente alto no produjo altas tasas de crecimiento económico en el periodo 1960 - 2000, comparado con los casos del grupo de países del Este asiático y el grupo de países de Medio Oriente y Norte de África, donde con menos años de escolaridad que los latinoamericanos se observaron mayores tasas de crecimiento que en estos últimos. Al parecer, la calidad de la educación afectó positivamente a la tasa de crecimiento económico más que la cantidad de años de escolarización.
Este artículo se aplica al caso de Colombia, desagregando el análisis para sus unidades político-administrativas -departamentos-. En ese sentido, para estudiar el papel que juega la educación en el crecimiento económico se emplea como base la estructura utilizada por Hanushek y Woessmann (2012a), en la cual se mezclan elementos teóricos y empíricos tanto de modelos de crecimiento endógeno como los de Lucas (1988), Romer (1990) y Aghion y Howitt, (1998), como también de modelos de crecimiento neoclásico como el de Mankiw et al. (1992). No obstante, aquí se utilizará una versión de esa estructura que se basa mucho más en el modelo aumentado de Solow utilizado en Mankiw, Romer y Weil, el cual resulta muy similar al modelo empleado por Breton (2015).
A. El modelo
Partimos de una función de producción neoclásica Cobb-Douglas tal como
donde Y it es la producción agregada del departamento i en el año t, K it es el stock de capital físico, H it es el stock de capital humano, L it es el trabajo y A it es el nivel de tecnología. Entonces, A it L it es el número de trabajadores efectivos. A y L crecen a una tasa constante m y n, respectivamente.
Mankiw et al. (1992) suponen que se invierte en capital físico una fracción constante de la producción, s k , y se invierte en capital humano también una fracción constante de la producción, s h . Definen el stock de capital por trabajador efectivo como k = K/AL, el stock de capital humano por trabajador efectivo como h = H/AL, y el nivel de producción por trabajador efectivo como y = Y /AL. El stock de capital físico se deprecia a una tasa δ k , y el stock de capital humano se deprecia a la tasa δ h . Entonces, la evolución de k y h se rige por:
A partir de las ecuaciones 2a y 2b puede obtenerse el stock de capital físico por trabajador efectivo del estado estacionario, k ss , y el stock de capital humano por trabajador efectivo del estado estacionario, h ss , respectivamente. Seguidamente, se sustituye cada una de esas expresiones en la función de producción y se aplican logaritmos para, finalmente, obtener el ingreso per cápita del estado estacionario, y ss
Mankiw et al. (1992) obtienen una versión dinámica del modelo, donde el crecimiento económico converge hacia el estado estacionario2, en el que λ representa la velocidad o tasa de convergencia:
Y, sustituyendo la ecuación (3) en la ecuación (4), se llega a un modelo de crecimiento como el de Solow ampliado:
Las tasas de inversión s k y s h pueden tomarse como el flujo de recursos de capital físico y de capital humano hacia la economía entre el periodo 0 y el periodo t. Este modelo incluye una variable de ingreso per cápita del periodo inicial, como en los modelos neoclásicos más comunes, con el objetivo de tener en cuenta posible convergencia entre el ingreso per cápita de los departamentos colombianos en el tiempo. A diferencia de Hanushek y Kimko (2000), Hanushek y Woessmann (2008, 2012a, 2012b), Breton (2011, 2015), Altinok y Aydemir (2017), entre otros, quienes usaron datos de corte transversal, el modelo aquí propuesto se contrasta con un panel que incluye la dimensión espacial (datos para 22 Departamentos colombianos), junto con una dimensión temporal, (datos para el periodo 2000-2019).
Una versión muy simple de la ecuación (5), recurriendo a la intuición de Nelson y Phelps (1966) y Hanushek y Woessmann (2012a), puede ser estimada empíricamente como:
donde, la tasa de crecimiento anual del PIB per cápita departamental, g, está en función de la tasa de inversión en capital físico, la tasa de inversión en capital humano, y las tasas de variación de algunas otras variables de control usualmente incluidas en modelos de la literatura sobre crecimiento, las cuales recoge la variable X. Específicamente, X aquí incluye factores tales como el nivel inicial del PIB per cápita del departamento y otros factores estructurales de la economía y las instituciones económicas, tales como el nivel de exportaciones de bienes y servicios y la tasa de homicidios.
Como se mencionó antes, Hanushek y Kimko (2000) y Hanushek y Woessmann (2008) -partiendo de una amplia revisión de la literatura de funciones de producción de educación- introducen una forma de modelizar el capital humano, H, a través de las habilidades cognitivas, representadas por los puntajes en las pruebas estandarizadas de conocimientos y habilidades, la cual se revela mucho más completa que anteriores interpretaciones. Hanushek y Woessmann (2012a) describen el origen de esas habilidades a través de la interacción de cuatro tipos de insumos: factores familiares (F ), cantidad (S) y calidad de la educación (q) -esto es qS-, las capacidades individuales (A), y otros factores determinantes (Z), tales como experiencia laboral y estado de salud, así:
Sin embargo, el capital humano no se puede observar directamente, y al ser una variable latente se requiere una medida correcta para probar su impacto en el crecimiento económico. En este sentido, el hecho de contar con resultados anuales de las pruebas Saber 11, -pruebas estandarizadas aplicadas a cada uno de los estudiantes de último año de la educación secundaria en Colombia-, ofrecen la posibilidad de ser utilizadas como medidas directas de las habilidades cognitivas como un indicador del capital humano en la ecuación (6), en vez de estimar los componentes de la ecuación 7 para evaluar las diferencias entre departamentos. Existen importantes ventajas al usar las habilidades cognitivas de los estudiantes que participan en este tipo de pruebas como una manera de medir indirectamente el capital humano. En Hanushek y Woessmann (2012a) se relacionan algunas de ellas.
No obstante, de manera complementaria, y con el objetivo de medir concretamente el efecto que el capital humano tiene sobre el crecimiento del PIB per cápita, aquí se compara también el efecto del capital humano medido por las habilidades cognitivas con el efecto del capital humano medido por los años promedio de escolaridad de la población de 15 años o más.
B. Datos y metodología
El modelo de crecimiento de la ecuación 6 se estima para 22 departamentos colombianos en el periodo 2000-20193. Para los departamentos restantes no se logró recopilar datos completos de todas las variables empleadas ni durante todo el periodo de tiempo estudiado. No hay antecedentes sobre trabajos que estimen el efecto de las habilidades cognitivas en el crecimiento económico a escala departamental en un periodo amplio como el que aquí se estudia.
Los datos del PIB per cápita por departamento se construyeron a partir de la serie retropolada de PIB por departamento, año base 2015, publicada por el Departamento Administrativo Nacional de Estadística, DANE (s.f.d), entidad oficial de estadísticas del Estado. Para obtener el PIB per cápita constante departamental se dividieron esas series por los datos de población provenientes de las proyecciones de población departamentales del DANE (s.f.c). Los datos sobre la inversión en capital físico se construyeron a partir de dos fuentes: sumando los datos de inversión en capital físico presentes en los microdatos por establecimiento industrial de cada departamento provenientes de la Encuesta Anual Manufacturera, EAM, publicada por el DANE (s.f.), con los datos de inversión municipal de la base de datos Terridata del Departamento Nacional de Planeación, DNP (s.f.). En este último caso, las series departamentales se construyeron sumando la información de todos los municipios de cada departamento para cada uno de los años estudiados. Dado que la información proveniente de esas dos bases de datos se encuentra en precios corrientes, se deflactó a nivel departamental obteniendo series a precios constantes. Seguidamente, se dividieron los datos resultantes sobre las series departamentales de PIB constante para obtener finalmente los datos departamentales anuales de la inversión en capital físico como porcentaje del PIB.
Los datos de las habilidades cognitivas se obtuvieron a partir de las bases de datos publicadas por el Instituto Colombiano para la Evaluación de la Educación (ICFES, s.f.), donde se encuentran los resultados por semestre del universo de individuos que presentaron la prueba Saber 11 desde el año 2000 hasta el 2019. La cifra total ascendió a 10 299128 resultados de pruebas individuales. En la prueba Saber 11 se evalúan todos los estudiantes que cursan el último año de la educación secundaria, tanto de colegios públicos como privados, sobre materias tales como matemáticas, biología, física, química, lenguaje, filosofía, historia, geografía e idioma extranjero (inglés). No obstante, a lo largo del periodo estudiado algunas de las materias evaluadas así como algunas agrupaciones de ellas fueron objeto de modificación por parte del ICFES. Por lo anterior, y con el objetivo de contar con datos homogéneos pero también similares a los de la literatura internacional, se procedió a agrupar las distintas materias en cinco áreas más generales: matemáticas, ciencias naturales (promedio de biología, física, química), lenguaje, ciencias sociales (promedio de filosofía, historia, geografía) e idioma extranjero, para cada departamento en cada uno de los años4. Para obtener el dato de cada año por departamento, primero se obtuvo el promedio del puntaje por área de todos los individuos que la presentaron en cada semestre del año. Seguidamente, se promediaron los dos semestres para obtener un solo dato del año. Finalmente, se promedió el puntaje de las cinco áreas obteniendo el puntaje promedio total. Sin embargo, se construyó otra serie departamental de habilidades cognitivas para todo el periodo, similar a la anterior, que obedece al promedio de los puntajes de las tres áreas evaluadas en las pruebas PISA.
No obstante, para que la evaluación del impacto de las habilidades cognitivas en el crecimiento económico sea exacta se necesitaría medidas de las habilidades de los trabajadores que conforman la población económicamente activa. Al no contar con evaluaciones de este tipo se debe hacer uso de una medida aproximada como la anterior.
Los datos sobre nivel de escolaridad de la población de 15 años y más se construyeron a partir de dos fuentes: la Encuesta Continua de Hogares, ECH (periodo 2000-2006) y la Gran Encuesta Integrada de Hogares, GEIH (periodo 2007-2019), ambas publicadas por el DANE (s.f.a; s.f.b). A partir de los microdatos anonimizados con periodicidad mensual se extrajo la información sobre los años de escolaridad cursados y aprobados por cada uno de los individuos de 15 años y más incluidos en la encuesta, los cuales se promediaron aritméticamente obteniendo un dato mensual por departamento. Seguidamente se procedió a promediar los datos mensuales obtenidos para condensarlos en datos anuales y así contar con las series completas para el periodo 2000-2019 de los 13 departamentos más importantes de Colombia, (incluida Bogotá D. C.)5. A diferencia de todas las demás variables de las que se pudo tener series anuales para los 22 departamentos, los años de escolaridad, dada la limitación estadística, solo se logró para 13 de ellos.
Las medidas más comunes del marco institucional utilizadas en la literatura son la apertura de la economía al comercio internacional y el imperio de la ley. En cuanto a la primera, no existe variabilidad en la legislación del comercio internacional entre los departamentos colombianos, pero sí en el desarrollo exportador a lo largo de los años. En este sentido, se utilizarán los datos de exportaciones de la base de datos SIEX de la Dirección de Impuestos y Aduanas Nacionales, DIAN (s.f.), de la sección “Exportaciones totales por Departamento de origen”, expresadas en dólares FOB. Por su parte, los datos referentes a la tasa de homicidios (proxy del índice de imperio de la ley) son el total de homicidios anuales ocurridos por Departamento, por cada 100 000 habitantes. Se obtuvieron de la base de datos Forensis del Grupo Centro de Referencia Nacional sobre Violencia adscrito al Instituto Nacional de Medicina Legal y Ciencias Forenses de Colombia (s.f.).
III. Resultados empíricos
A. Resultados iniciales
Los resultados empíricos se obtuvieron a partir de estimaciones de un panel de datos con 22 departamentos durante el periodo 2000-2019.6 Solo en los casos en los que se compara el impacto de las dos variables de capital humano sobre el crecimiento económico la estimación se hizo para 13 departamentos debido a la limitación que se tiene con los datos de años promedio de escolaridad. Igualmente, se evaluó el impacto de la inversión en capital físico, el volumen de las exportaciones y la tasa de homicidios sobre la tasa de crecimiento del PIB per cápita. El nivel inicial de PIB per cápita también se incluyó en las regresiones como variable explicativa para evaluar la presencia de convergencia condicional entre los departamentos colombianos en el periodo analizado.
La Tabla 1 presenta los resultados de la estimación de un modelo de crecimiento simple log-log con habilidades cognitivas, años promedio de escolaridad, inversión en capital físico como porcentaje del PIB y PIB per cápita del año 2000 (esta última con el fin de contrastar convergencia condicional entre los departamentos colombianos) mediante el estimador Hausman-Taylor.
Tabla 1
Capital humano y crecimiento económico en departamentos de Colombia (2000-2019)
[i]Notas: Variable dependiente: logaritmo natural del PIB per cápita constante departamental anual. Entre paréntesis se presentan los errores estándar. Todas las regresiones incluyen una constante, y fueron estimadas con el estimador Hausman-Taylor. Habilidades cognitivas es el promedio de todas las áreas evaluadas en la prueba Saber 11. *Significatividad estadística al 10 %. **Significatividad estadística al 5 %. ***Significatividad estadística al 1 %.
Se estimó un modelo de efectos fijos, así como un modelo de efectos aleatorios, y se sometieron al test de Hausman buscando determinar la especificación más apropiada. El resultado ocasionó un dilema, puesto que, por una parte, el estimador de efectos aleatorios fue inconsistente dada la correlación entre las variables explicativas y tales efectos aleatorios, lo cual indicaba que la solución al problema era usar el estimador de efectos fijos; por otra, tal resolución significaba que ya no se podría estimar el efecto del PIB per cápita inicial para contrastar convergencia condicional, la cual es una variable invariante en el tiempo, puesto que era eliminada de la estimación con efectos fijos debido a colinealidad. Ese inconveniente se solucionó recurriendo al estimador Hausman-Taylor, el cual emplea variables instrumentales y se aplica al modelo de efectos aleatorios para resolver el problema de inconsistencia que surge a partir de la correlación entre algunas variables explicativas y los efectos aleatorios. Gracias al uso de esta técnica se logró estimar un modelo muy similar al de efectos fijos sin que fuera eliminada aquella variable que es invariante en el tiempo, obteniendo coeficientes de los parámetros muy robustos y de magnitud similar a los del estimador within.
La columna 1 presenta los resultados de la estimación del modelo inicial con el puntaje promedio de las cinco grandes áreas evaluadas en las pruebas Saber 11 explicando la tasa de crecimiento del PIB per cápita de los 22 departamentos. Este coeficiente es alto (0,85) y estadísticamente significativo al 1 %, reflejando la fuerte influencia de las habilidades cognitivas en el crecimiento económico departamental. Así mismo, la variable que indica la participación de la inversión en capital físico en el PIB departamental resulta altamente significativa y la magnitud del coeficiente (0,200) es aproximadamente una cuarta parte de aquel del puntaje en la prueba. La columna 2 muestra los resultados de la estimación del mismo modelo, pero esta vez se evalúa la influencia de los años promedio de escolaridad de la población de 15 años y más en el crecimiento económico departamental, en vez de las habilidades cognitivas, para los 13 departamentos con datos completos. El coeficiente de los años de escolaridad es de mayor magnitud que el de los resultados de la prueba Saber 11 de la columna 1, y también es estadísticamente significativo al 1 %. No obstante, la inversión en capital físico se reduce casi a cero y pierde la significatividad estadística, algo que ocurre también al incluir en la regresión las dos variables de capital humano juntamente en la columna 3. En este caso, los años de escolaridad, así como las habilidades cognitivas, son estadísticamente significativas al 1 %, si bien la primera exhibe un coeficiente de mayor magnitud, reflejando una mayor influencia en la tasa de crecimiento departamental.
Por otra parte, las tres especificaciones de la Tabla 1 no proporcionan evidencia de convergencia condicional entre los departamentos colombianos durante el periodo 2000-2019, pues el coeficiente del PIB per cápita del año 2000 es positivo y estadísticamente significativo al 1 %, evidenciando -más bien- un proceso de divergencia entre el PIB per cápita de los departamentos durante estas dos décadas. Finalmente, el modelo goza de significatividad conjunta (Prob > Chi 2 = 0, 000).
En la Tabla 2 se presentan los resultados de la estimación de un modelo similar al anterior, pero esta vez se amplía añadiendo dos variables de control que permitan una mejor especificación del modelo de crecimiento, en línea con los trabajos más actuales a nivel internacional. Así, los resultados en la columna 1 muestran que el coeficiente de las habilidades cognitivas sigue siendo alto y significativo al 1 %, mientras que las nuevas variables dejan ver su relevante papel en la explicación del crecimiento económico de los departamentos de Colombia. En este sentido, las exportaciones y la tasa de homicidios (por cada cien mil habitantes) resultan estadísticamente significativas al 1 % y tienen los signos esperados, indicando un efecto positivo de las exportaciones sobre el crecimiento económico y un efecto negativo de la tasa de homicidios del doble del tamaño de las exportaciones sobre la tasa de crecimiento del PIB departamental en estas dos décadas.
Tabla 2
Habilidades cognitivas, logro escolar y crecimiento económico
[i]Notas: Variable dependiente: logaritmo natural del PIB per cápita constante departamental anual. Entre paréntesis se presentan los errores estándar. Todas las regresiones incluyen una constante. Las columnas 1 a la 4 fueron estimadas con el estimador Hausman-Taylor; las columnas 5 y 6 fueron estimadas con el estimador within (efectos fijos). *Significatividad estadística al 10 %. **Significatividad estadística al 5 %. ***Significatividad estadística al 1 %. (a): El puntaje de la prueba Saber 11 es el promedio de las tres áreas que se evalúan en las pruebas PISA: matemáticas, ciencias naturales y lenguaje. (b): El puntaje de la prueba Saber 11 es el promedio de las tres áreas que se evalúan en las pruebas PISA: matemáticas, ciencias naturales y lenguaje.
En la columna 2 se estima el mismo modelo con las dos variables de control anteriores, pero ahora se sustituyen las habilidades cognitivas por los años promedio de escolaridad, o logro escolar. Los años de escolaridad exhiben un coeficiente ligeramente menor que las habilidades cognitivas de la columna 1. Las exportaciones y la tasa de homicidios siguen teniendo un papel muy importante en la determinación de la tasa de crecimiento económico en esta nueva especificación, si bien el coeficiente de las primeras esta vez es el doble (0,07) que en la columna 1. En este caso, la inversión se vio afectada al reducirse notablemente su coeficiente y significatividad estadística. Los resultados mostrados en las columnas 3 y 4 permiten comparar el efecto de las habilidades cognitivas frente al efecto de los años de escolaridad sobre el crecimiento económico departamental.
Un hallazgo muy relevante es que, con la especificación completa del modelo de crecimiento, las habilidades cognitivas parecen ser más influyentes en el crecimiento económico (0,52) que los años de escolaridad (0,46). Este resultado se refuerza en la columna 4, donde las habilidades cognitivas se miden como el promedio de solo tres áreas evaluadas (matemáticas, ciencias naturales y lenguaje) tal como se evalúa en las pruebas PISA.
Así, parece evidente que -aunque ambas medidas tienen signo positivo y son estadísticamente muy significativas- la calidad de la educación es más importante que la cantidad de educación. Estos resultados son similares a los obtenidos por Altinok y Aydemir (2017) y Breton (2015) en sus estudios entre países. Por otra parte, en las columnas 1 a la 4, nuevamente no hay evidencia de convergencia condicional entre los departamentos entre el año 2000 y 2019 -tal como ocurrió con los resultados de Tabla 1- mostrando más bien un proceso de divergencia entre el PIB per cápita de los Departamentos en estos veinte años.
Ante estos últimos resultados, en las columnas 5 y 6 se excluye el PIB per cápita del año 2000 (variable empleada para contrastar convergencia condicional) y se estiman las regresiones mediante el estimador within (efectos fijos), pues ya no se hace necesario utilizar el estimador Hausman-Taylor. Los resultados son similares a los de las columnas 3 y 4 aunque la diferencia entre el efecto de las habilidades cognitivas y el de los años de escolaridad se hace mayor, es decir, el coeficiente de los puntajes en las pruebas aumenta ligeramente y el del logro escolar disminuye. En términos generales, la calidad del modelo es buena pues las variables independientes explican en gran medida la varianza de la tasa de crecimiento del PIB per cápita departamental anual (R2 = 0,91).
Los resultados de las columnas 4 y 6 de la Tabla 2 permiten advertir que las habilidades y competencias que se adquieren en algunas áreas del conocimiento pueden influir en mayor grado en el crecimiento económico que las que se aprenden en otras áreas del saber. En este sentido, Jamison et al. (2007) y Hanushek y Woessmann (2012a), entre otros, encontraron evidencia de que mayores conocimientos y competencias en áreas como matemáticas y ciencias (naturales) influyen en mayor medida sobre el proceso de crecimiento económico, ya que permiten acelerar el progreso tecnológico de un país. En este caso concreto, el promedio del puntaje obtenido por los jóvenes colombianos en las pruebas de matemáticas, ciencias naturales y lenguaje jugaron un papel más determinante que el promedio del puntaje obtenido en todas las áreas evaluadas donde además se incluye ciencias sociales e idioma inglés. Este hecho llevó a modificar la especificación de las habilidades cognitivas y estimar el efecto de cada una de las cinco áreas por separado.
La columna 1 de la Tabla 3 muestra los resultados de la estimación del modelo de crecimiento con las habilidades cognitivas representadas por el puntaje promedio obtenido por todos los individuos en las pruebas Saber 11 en el área de matemáticas para cada uno de los 22 departamentos de la muestra y para cada uno de los 20 años del periodo estudiado. La columna 2 hace lo propio para el caso de ciencias naturales, y así sucesivamente hasta la columna 5, donde se estima el puntaje en la prueba de inglés. Inicialmente, se debe resaltar la relación robusta existente entre las variables explicativas y la tasa de crecimiento económico de los departamentos colombianos. Los coeficientes de las variables de control (inversión en capital físico, nivel de exportaciones y tasa de homicidios), así como sus errores estándar, presentan una muy leve variación a través de las cinco diferentes especificaciones. También, todos los coeficientes en cada una de las regresiones son estadísticamente significativos al 1 %, y los R2 se encuentran entre 0,54 y 0,58. No obstante, se observan importantes diferencias entre los coeficientes de las cinco áreas evaluadas, siendo matemáticas, lenguaje y ciencias naturales, en ese orden, los de mayor magnitud.
Tabla 3
Habilidades cognitivas según áreas del conocimiento y su efecto económico departamental
[i]Notas: Variable dependiente: logaritmo natural del PIB per cápita constante departamental. Entre paréntesis se presentan los errores estándar. Todas las regresiones incluyen una constante. *Significatividad estadística al 10 %. **Significatividad estadística al 5 %. ***Significatividad estadística al 1 %.
Tal como se apuntaba más arriba acerca de los hallazgos de Jamison et al. (2007) y Hanushek y Woessmann (2012a), en los departamentos colombianos también parece haber una mayor influencia de los conocimientos y competencias adquiridos en matemáticas, lenguaje y ciencias naturales sobre el crecimiento económico de las últimas dos décadas. No obstante, se puede ir un poco más allá en el entendimiento de la anterior relación entre algunas de las áreas del conocimiento evaluadas y las más altas tasas de crecimiento departamental en Colombia.
B. Diferentes sub-muestras de departamentos
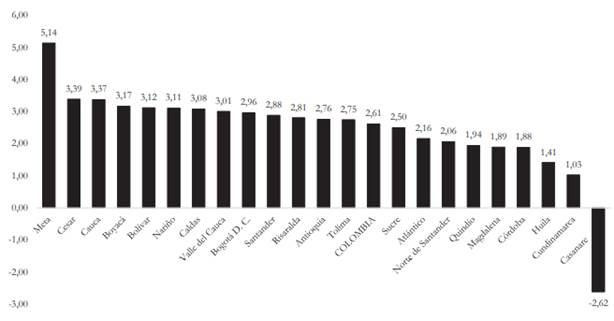
Sería interesante averiguar qué sucede al incluir en una regresión solo los departamentos colombianos con las tasas de crecimiento del PIB per cápita más altas en el periodo estudiado y evaluar el mismo modelo de crecimiento. Esto se hizo y se tuvo en cuenta a los departamentos que tuvieron una tasa de crecimiento promedio entre 2000 y 2019 superior a 3 %, esto es: Meta, Cesar, Cauca, Boyacá, Bolívar, Nariño, Caldas y Valle (ver Figura 1). Los resultados se muestran en la Tabla 4. En las columnas 1 a 5 se estima por separado los puntajes de cada una de las cinco áreas, mientras que en la columna 6 se muestran los resultados para el promedio de todas las áreas evaluadas, y en la columna 7 los resultados para el promedio de tres áreas: matemáticas, ciencias naturales y lenguaje.
Tabla 4
Departamentos con las mayores tasas de crecimiento: efecto de las habilidades cognitivas
[i]Notas: Variable dependiente: logaritmo natural del PIB per cápita constante departamental de los ocho Departamentos con tasas de crecimiento superiores a 3 %. Entre paréntesis se presentan los errores estándar. Todas las regresiones incluyen una constante. *Significatividad estadística al 10 %. **Significatividad estadística al 5 %. ***Significatividad estadística al 1 %. a: El puntaje de la prueba Saber 11 es el promedio de todas las áreas que se evalúan por el ICFES: matemáticas, ciencias naturales, sociales, lenguaje e inglés. b: El puntaje de la prueba Saber 11 es el promedio de las tres áreas que se evalúan en las pruebas PISA: matemáticas, ciencias naturales y lenguaje.
No sorprende que las áreas que se muestran más relacionadas con el crecimiento económico en los departamentos con las más altas tasas de aumento del PIB per cápita sean nuevamente las mismas tres, solo que esta vez es el puntaje en lenguaje el que ostenta el mayor coeficiente, seguido por matemáticas y ciencias naturales. También, se observa que los parámetros de cada una de las cinco áreas, así como del promedio total y del promedio de las tres son mayores en esta sub-muestra (entre un 10 % y un 20 %) que con la muestra completa de 22 departamentos. De manera interesante, las exportaciones influyen mucho más (casi 4 veces) en el crecimiento de estos ocho departamentos que en la muestra de los 22. Algo similar ocurrió con la inversión en capital físico, aunque el aumento en este caso fue menor. Por el contrario, la tasa de homicidios redujo su influencia en el crecimiento respecto a la muestra más grande de entes territoriales mostrado en la Tabla 3, a la vez que la significatividad estadística baja del 1 % al 5 % en los casos del puntaje en matemáticas, ciencias naturales y lenguaje. Finalmente, debe resaltarse que de forma global las variables independientes explican en mayor medida la varianza de la tasa de crecimiento anual del PIB per cápita de estos ocho departamentos, (R2 entre 0,85 y 0,87), que en el caso de los 22, (R2 entre 0,54 y 0,58).
Estos resultados invitan a inquirir lo que pudo haber pasado en otro contexto, por ejemplo, en el caso de las mayores economías departamentales de Colombia7. Es decir, si el efecto de las habilidades cognitivas sobre el crecimiento económico en los departamentos con mayor nivel de PIB real es similar al observado en aquellos con las mayores tasas de crecimiento. Cabe resaltar que en estos dos conjuntos de entes territoriales solo es común el departamento del Valle. Los resultados de las nuevas estimaciones se presentan a continuación.
La Tabla 5 tiene la misma estructura y distribución de columnas que la Tabla 4, mientras que los resultados son diferentes entre ambas. Como primera medida, los coeficientes de las siete diferentes especificaciones de habilidades cognitivas son entre 30 % y 35 % menores que en el caso de los departamentos con las tasas más altas de crecimiento de la Tabla 4. Otros aspectos a destacar tienen que ver, primero, con la influencia de la tasa de homicidios sobre el crecimiento, pues en este caso su efecto negativo aumenta al doble de lo encontrado en el caso los departamentos con mayores tasas de crecimiento, indicando una mayor sensibilidad del crecimiento económico en las 6 economías departamentales más grandes de Colombia ante variables de violencia, orden y seguridad; y segundo, el papel de las exportaciones.
En todas las especificaciones se nota un descenso de alrededor del 40 % en su efecto positivo sobre el crecimiento de las economías más importantes del país respecto a los resultados de la Tabla 4, lo cual podría indicar que las más altas tasas de crecimiento del PIB per cápita de los departamentos colombianos en las primeras dos décadas del siglo XXI fueron guiadas principalmente por las habilidades cognitivas de sus trabajadores y por los mayores niveles de sus ventas al exterior. El efecto positivo de la inversión en capital físico no mostró variaciones importantes entre las dos sub-muestras.
En lo que respecta a los resultados sobre los efectos de las habilidades cognitivas separando las cinco áreas evaluadas en las pruebas Saber 11 -columnas 1 a 5- cambia el orden de importancia respecto a lo observado antes en las Tablas 3 y 4. Aparece esta vez en primer lugar el resultado en la prueba de lenguaje seguido por los de ciencias naturales, matemáticas, inglés y sociales. De nuevo, las tres áreas que han venido siendo las de mayor efecto sobre el crecimiento vuelven a demostrarlo esta vez. Además, el área de ciencias sociales es la que exhibe el menor coeficiente, tal como en las Tablas 3 y 4. Finalmente, y no menos importante, todos los coeficientes en las diferentes especificaciones son estadísticamente significativos al 1 %. De esta forma, se sigue observando coherencia a través de las diferentes muestras espaciales en cuanto a la importancia de las habilidades y competencias en matemáticas, ciencias naturales y lenguaje para influir en el crecimiento del PIB per cápita departamental en Colombia, en línea con los resultados de trabajos a nivel internacional utilizando muestras de países desarrollados y países en desarrollo.
Tabla 5
Mayores economías departamentales: efecto de las habilidades cognitivas sobre el crecimiento económico
[i]Notas: Variable dependiente: logaritmo natural del PIB per cápita constante departamental de los seis Departamentos con el nivel promedio de PIB per cápita superior al nivel promedio nacional. Todas las regresiones incluyen una constante. *Significatividad estadística al 10 %. **Significatividad estadística al 5 %. ***Significatividad estadística al 1 %. a: El puntaje de la prueba Saber 11 es el promedio de todas las áreas que se evalúan por el ICFES: matemáticas, ciencias naturales, sociales, lenguaje e inglés. b: El puntaje de la prueba Saber 11 es el promedio de las tres áreas que se evalúan en las pruebas PISA: matemáticas, ciencias naturales y lenguaje.
Conclusiones
En las últimas tres décadas se ha publicado una amplia cantidad de estudios empíricos indagando acerca de la relación entre el capital humano y la tasa de crecimiento económico entre países empleando como proxy, primero, información sobre la tasa de matriculación, luego, datos sobre los años de escolaridad alcanzados por la población en edad de trabajar, y más recientemente, utilizando las habilidades cognitivas de la población trabajadora. Fue precisamente, a partir del estudio pionero de Hanushek y Kimko (2000), que se conoció empíricamente la gran importancia que tienen las habilidades cognitivas -resultados en pruebas estandarizadas de conocimientos y habilidades- de la futura fuerza laboral sobre las tasas de crecimiento económico.
Este artículo prueba, en el contexto de los departamentos colombianos, el efecto estimado de las habilidades cognitivas sobre el crecimiento económico que se ha hecho en trabajos a nivel internacional empleando muestras amplias de países. Además, contrasta la heterogeneidad de dichos efectos en razón de: a) las diferentes áreas del conocimiento evaluadas en las pruebas Saber 11 que se incluyan en las regresiones, y b) diferentes agrupaciones de departamentos basadas en tasas de crecimiento del PIB por habitante y tamaño de sus economías. Esto se hizo posible con la construcción de una amplia base de datos para 22 departamento durante el periodo 2000-2019 con información proveniente de fuentes oficiales nacionales de variables tales como, PIB real per cápita, inversión en capital físico como porcentaje del PIB, años de escolaridad de población con 15 años y más (para 13 entes territoriales), habilidades cognitivas (puntajes en pruebas Saber 11, promedio total y desagregados por área del conocimiento), valor de las exportaciones y tasa de homicidios por cada 100 000 habitantes.
El análisis produjo cinco resultados principales: a) el capital humano medido por las habilidades cognitivas tiene un gran efecto positivo y estadísticamente significativo sobre la tasa de crecimiento económico de los 22 departamentos colombianos en el periodo 2000-2019; b) el capital humano medido por los años de escolaridad también muestra un efecto positivo y estadísticamente significativo en el ritmo de expansión del PIB per cápita, aunque de menor magnitud que el observado en las habilidades cognitivas; c) algunos tipos de habilidades cognitivas (matemáticas, lenguaje y ciencias naturales) presentan mayores efectos positivos sobre el crecimiento que otras, como es el caso de ciencias sociales; d) los efectos positivos de las distintas clases de habilidades cognitivas sobre el crecimiento económico -en general- son mayores en los departamentos con las tasas de crecimiento más altas que en aquellos económicamente más grandes; e) se presenta un efecto positivo y significativo, en general, de la tasa de inversión en capital físico sobre el crecimiento económico. Así mismo, el nivel de exportaciones influye de forma positiva y la tasa de homicidios de forma negativa (ambos estadísticamente significativos al 1 %) sobre la tasa de crecimiento del PIB per cápita de los departamentos.
Estos hallazgos tienen varias implicaciones de política. En primer lugar, la promoción de políticas educativas que se centren en aumentar la calidad de la educación tendrá mayores efectos sobre el crecimiento económico que aquellas que sólo busquen lograr más años de educación en la población. Según Pritchett (2001), si la calidad de la educación es muy baja no producirá las habilidades necesarias en la fuerza laboral que impulsen un mayor crecimiento económico. Por tanto, si se persiguen los dos objetivos conjuntamente, los efectos positivos serán mucho mayores. De igual manera, las políticas educativas deben enfocarse en la formación de profesores con altas cualificaciones técnicas y didácticas en áreas cómo matemáticas, lenguaje y ciencias naturales, pues esto ayudaría a ofrecer a los estudiantes altos estándares de calidad en las tres áreas que más influyen en el crecimiento económico. En tercer lugar, las economías departamentales más pequeñas y aquellas otras con bajas tasas de crecimiento del PIB per cápita pueden conseguir mayores ritmos de crecimiento económico si mejoran la calidad de su sistema educativo, principalmente en la formación de conocimientos, habilidades y competencias en áreas como matemáticas, lenguaje y ciencias naturales en sus estudiantes.