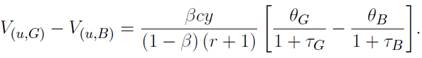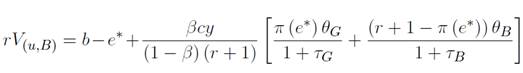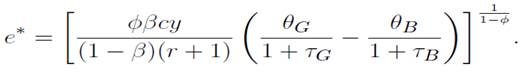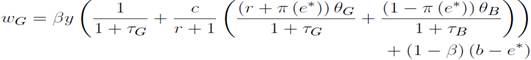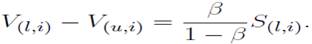Absenteeism and productivity: an experience-rating adjustment scheme applied to health insurance in France
DOI:
https://doi.org/10.17533/udea.le.n88a01Keywords:
health insurance, experience rating, productivity, search and matching modelsAbstract
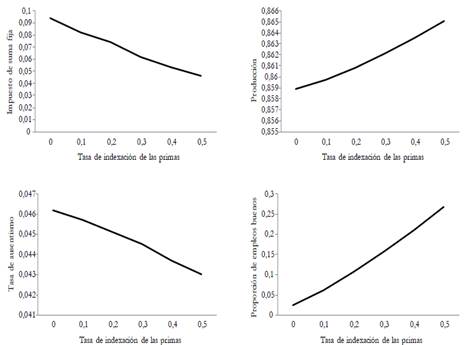
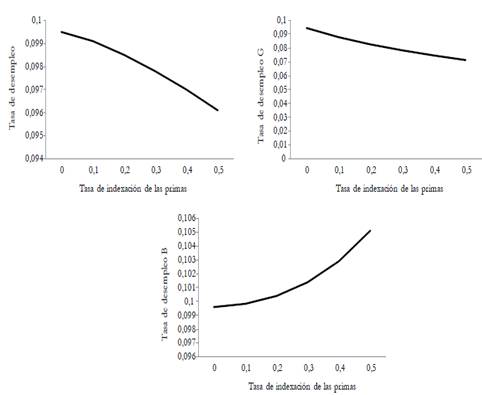
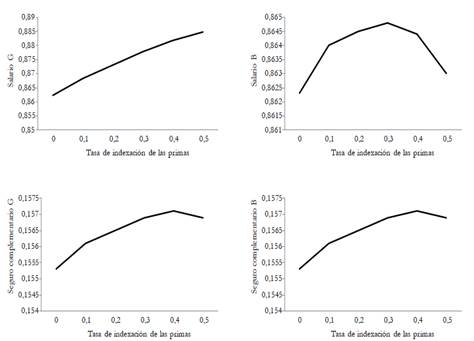
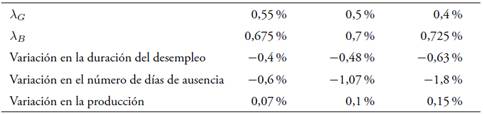
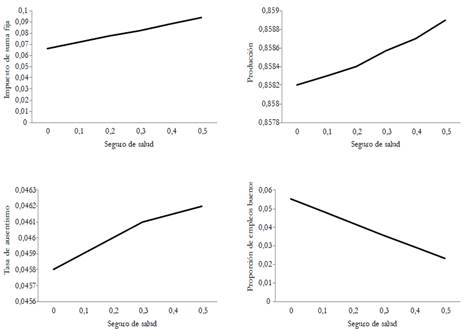
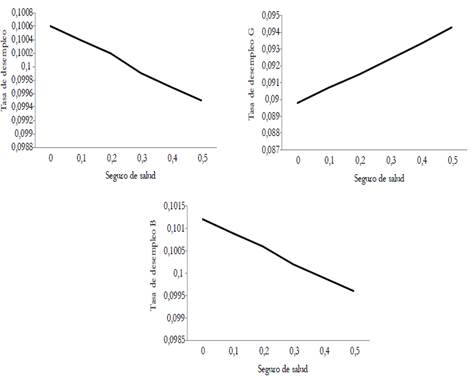
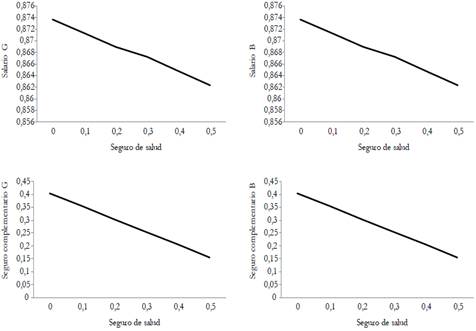
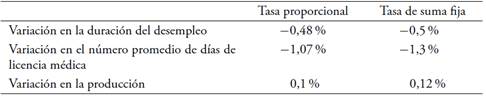
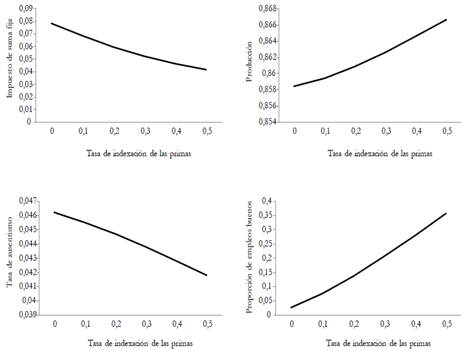
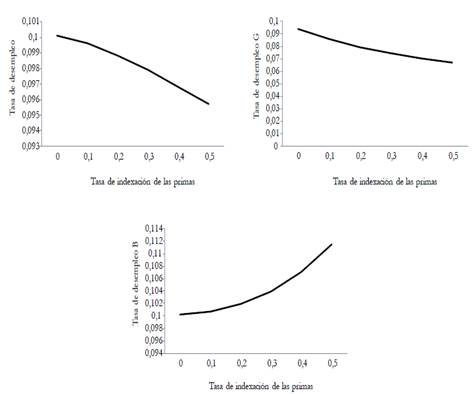
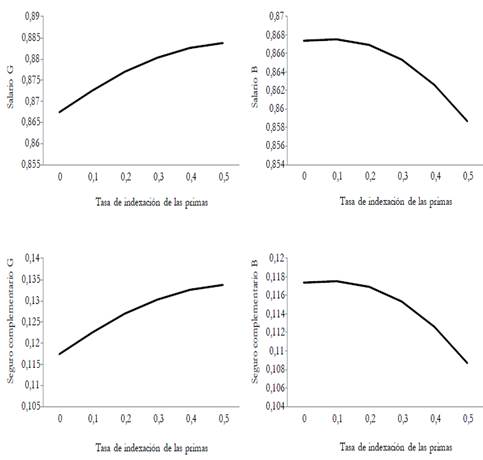
In this paper, we analyze the effects of introducing an experience-rating adjustment scheme on employers? contributions to health nsurance. To this end, we develop a search and matching model in a segmented labor market. In the segment with higher-risk jobs, sick leaves are more frequent and thereby average productivity is lower. The model is calibrated to the French economy. Results from the simulations show that the experience-rating policy slightly improves productivity and employment. In quantitative terms, a 1 % variation in the experience-rating rate induces a 0,48 % reduction in the unemployment spell, a 1,07 % reduction in the days of absence, and a 0.1 % increase in productivity. Finally, this policy also leads to a slightly better economic performance compared to health insurance privatization.
Downloads
References
Afsa, Cédric & Givord, Pauline (2009). “Le rôle des conditions de travail dans les absences pour maladie: Le cas des horaires irréguliers”, Economie et Prévision, Vol.187, No. 1, pp. 83-103.
Allen, Steven G. (1981). “An empirical model of work attendance”, The Review of Economics and Statistics, Vol. 63, No. 1, pp. 77-87.
Andreoni, James & Sprenger, Charles (2012). “Estimating Time Preferences from Convex Budgets”, American Economic Review, Vol. 102, No. 7, pp. 3333-3356.
Barlet, Muriel; Blanchet, Didier; Crusson, Laure; Givord, Pauline; Picart, Claude; Rathelot, Roland & Sillard, Patrick (2007). “Dossier: Flux de main-d’oeuvre, flux d’emplois et internationalisation [Édition: L’économie française – Comptes et dossiers]”, Insee Références, pp. 108-131.
Browning, Martin; Dano, Anne Moller & Heinesen, Eskil (2006). “Job displacement and stress-related health outcomes”, Health Economics, Vol. 15, No. 10, pp. 1061-1075.
Cahuc, Pierre & Le Barbanchon, Thomas (2010). “Labor market policy evaluation in equilibrium: Some lessons of the job search and matching model”, Labour Economics, Vol. 17, No. 1, pp. 196-205.
Comisión de las Comunidades Europeas (2007). Mejorar la calidad y la productividad en el trabajo: estrategia comunitaria de salud y seguridad en el trabajo (2007-2012). Recuperado de: https://goo.gl/R12c5s (Noviembre 10 de 2016).
Commission des Comptes de la Sécurité Sociale (ccss) (2016). Les comptes de la sécurité sociale. Résultats 2015. Prévisions 2016. Recuperado de : http://www.securite-sociale.fr/IMG/pdf/rapport-ccss-juin2016.pdf (Diciembre 17 2016).
Direction de l’Animation de la Recherche, des Études et des Statistiques (dares) (2013). “Les absences au travail des salariés pour raisons de santé: un rôle important des conditions de travail”, Dares Analyses, No. 009. Recuperado de: http://travail-emploi.gouv.fr/IMG/pdf/2013-009.pdf (Noviembre 10 de 2016).
De Raaf, Shawn; Motte, Anne & Vincent, Carole (2005). “A Literature Review of Experience-Rating Employment Insurance in Canada”, SRDC Working Paper Series, 05-03. Social Research and Demonstration Corporation.
Esler, Dietmar (Ed.) (2010), “Economic incentives to improve occupational safety and health: a review from the European perspective”, Working Environment Information. European Agency for Safety and Health at Work. Recuperado de: https://osha.europa.eu/en/tools-andpublications/publications/reports/economic_incentives_TE3109255ENC (Noviembre 4 de 2016).
Hosios, Arthur J. (1990). “On the Efficiency of Matching and Related Models of Search and Unemployment”, Review of Economic Studies, Vol. 57, No. 2, pp. 279–298.
Institut National de la Statistique et des Études Économiques (insee) (s.f.). Taux de chômage au sens du BIT - Ensemble - France métropolitaine et DOM - Données CVS. Recuperado de : https://www.insee.fr/fr/statistiques/serie/001688527 (Noviembre 10, 2016).
Joseph, Gilles (2005). “Critères d’attribution des allocations chômage et performances du marché du travail”, Annales d’économie et de statistique, No. 78, pp. 117-141.
Kankaanpää, Eila (2010). “Economic incentives as a policy tool to promote safety and health at work”, Scandinavian Journal of Work Environment and Health, Vol. 36, No. 4, pp. 319-324.
Katz, Lawrence F. & Meyer, Bruce D. (1990). “The impact of the potential duration of unemployment benefits on the duration of unemployment”, Journal of Public Economics, Vol. 41, No. 1, pp. 45-72.
Kuhn, Andreas; Lalive, Rafael & Zweimüller, Josef. (2009). “The public health costs of job loss”, Journal of Health Economics, Vol. 28, No. 6, pp. 1099-1115.
Lengagne, Pascale (2016). “Experience Rating and Work-related Health and Safety”, Journal of Labor Research, Vol. 37, No. 1, pp. 69-97.
Malakoff Médéric (s.f.). Les coûts de l’absentéisme. Recuperado de: https://entreprise-territoire-de-sante.malakoffmederic.com/absenteisme/info/couts-de-l-absenteisme (Noviembre 10 de 2016).
Mansfield, Elizabeth; MacEachen, Ellen; Tompa, Emile; Kalcevich, Christina; Endicottb, Marion & Yeung, Natalie (2012). “A critical review of literature on experience rating in workers’ compensation systems”, Policy and Practice in Health and Safety, Vol. 10, No. 1, pp. 3-25.
Monneuse, Denis (2015). L’absentéisme au travail. Afnor Editions.
Petrongolo, Barbara & Pissarides, Christopher A. (2001) “Looking into the black box: A survey of the matching function”, Journal of Economic Literature, Vol. 39, pp. 390-431.
Pissarides, Christopher A. (1990). Equilibrium Unemployment Theory. Oxford: Basil Blackwell.
Shapiro, Carl & Stiglitz, Joseph (1984). “Equilibrium unemployment as a worker discipline device”, The American Economic Review, Vol. 74, No. 3, pp. 433-444.
Strauss, John & Thomas, Duncan (1998). “Health, nutrition and economic development”, Journal of Economic Literature, Vol. 36, No. 2, pp. 766-817.
Organización Internacional del Trabajo (oit) (2009). Día Mundial de la Seguridad y la Salud en el Trabajo 2009. Información sobre seguridad y salud en el trabajo. Recuperado de: http://www.ilo.org/wcmsp5/groups/public/@dgreports/@dcomm/documents/publication/wcms_105149.pdf (Diciembre 20 de 2016).
Ose, Solveig Osborg (2005). “Working conditions, compensation and absenteeism”, Journal of Health Economics, Vol. 24, No. 1, pp. 161-188.
Van den Berg, Gerard J. (1990), “Nonstationarity in job-search theory”, Review of Economic Studies, Vol. 57, No. 2, pp. 255-277.
Vlassenko, Elisabeth & Willard, Jean-Charles (1984). “Absentéisme: le poids des facteurs collectifs”, Economie et Statistique, Vol. 164, No. 1, pp. 39-51.
Downloads
Published
How to Cite
Issue
Section
License
Copyright (c) 2017 Sébastien Ménard, Coralia Quintero

This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License.
This page, by Universidad de Antioquia, is licensed under a Creative Commons Attribution License.
Authors who publish with this journal agree to retain copyright and grant the journal right of first publication, with the article licensed under a Creative Commons Attribution-NonCommercial-ShareAlike License allowing others to share it as long as they acknowledge its authorship and original publication in this journal.
Authors can enter into separate, additional contractual arrangements for the non-exclusive distribution of the journal's published version of the work (e.g., post it to an institutional repository or publish it in a book), provided that these arrangements be not for profit and the journal be acknowledged as the original source of publication.
Authors are permitted and encouraged to post their papers online (e.g., in institutional repositories or on their websites), as it can lead to valuable exchanges as well as greater citation of the published work.







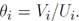 El supuesto de homogeneidad nos permite escribir la probabilidad de llenar una vacante,
qi
, como función de la tensión en el mercado de trabajo, dada por Entonces, un puesto vacante es llenado con
El supuesto de homogeneidad nos permite escribir la probabilidad de llenar una vacante,
qi
, como función de la tensión en el mercado de trabajo, dada por Entonces, un puesto vacante es llenado con 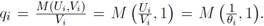 probabilidad
probabilidad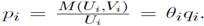
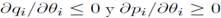 Los supuestos retenidos para la función de emparejamiento implican que reproduciendo asíla existencia de efectos de congestión en el mercado de trabajo.
Los supuestos retenidos para la función de emparejamiento implican que reproduciendo asíla existencia de efectos de congestión en el mercado de trabajo.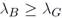 se cumple. Por lo tanto, como los trabajadores son idénticos, la diferencia
se cumple. Por lo tanto, como los trabajadores son idénticos, la diferencia 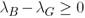 se debe únicamente a las diferencias entre las empresas en cuanto a sus condiciones de trabajo. Por otra parte, ψ representa la probabilidad de que un trabajador enfermo se cure, la cual es la misma para todos los trabajadores, dado que son homogéneos.
se debe únicamente a las diferencias entre las empresas en cuanto a sus condiciones de trabajo. Por otra parte, ψ representa la probabilidad de que un trabajador enfermo se cure, la cual es la misma para todos los trabajadores, dado que son homogéneos.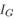 del segmento G y por los individuos
IB
del segmento B, y debido a la normalización se cumple que
del segmento G y por los individuos
IB
del segmento B, y debido a la normalización se cumple que  Los individuos pueden transitar de un segmento a otro solo durante los periodos de desempleo. En otros términos, los trabajadores desempleados tienen posibilidad de buscar empleo, ya sea sobre el segmento G o sobre el segmento B. Como la producción disminuye cuando el ausentismo aumenta, se deduce que el excedente o surplus es más importante en el segmento G, donde la tasa de ausentismo es menor, que en el segmento B. Por lo tanto, la situación de los desempleados del segmento G es siempre superior a la de los desempleados del segmento B.
Los individuos pueden transitar de un segmento a otro solo durante los periodos de desempleo. En otros términos, los trabajadores desempleados tienen posibilidad de buscar empleo, ya sea sobre el segmento G o sobre el segmento B. Como la producción disminuye cuando el ausentismo aumenta, se deduce que el excedente o surplus es más importante en el segmento G, donde la tasa de ausentismo es menor, que en el segmento B. Por lo tanto, la situación de los desempleados del segmento G es siempre superior a la de los desempleados del segmento B.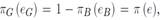 por lo que la probabilidad de volverse o seguir siendo un buscador de empleo en el segmento G requiere de cierto esfuerzo e > 0.
por lo que la probabilidad de volverse o seguir siendo un buscador de empleo en el segmento G requiere de cierto esfuerzo e > 0.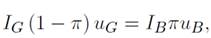
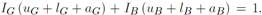 El equilibrio de los flujos de los trabajadores queda descrito como sigue:
El equilibrio de los flujos de los trabajadores queda descrito como sigue: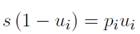

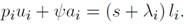
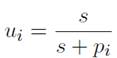
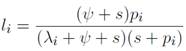
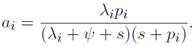
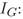
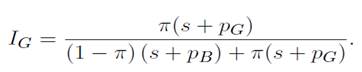
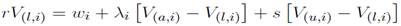
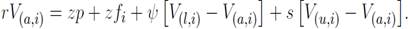
 debido a que se ausenta de su puesto de trabajo; finalmente, con probabilidad s, su puesto se destruye y pierde
debido a que se ausenta de su puesto de trabajo; finalmente, con probabilidad s, su puesto se destruye y pierde 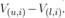 Así mismo, la ecuación (10) establece que un trabajador ausente recibe una indemnización pública zp y una indemnización complementaria por parte del empleador, zfi; con una probabilidad ψ se recupera de su enfermedad, en cuyo caso ganaría cierto bienestar; finalmente, enfrenta también una probabilidad s de perder su empleo.
Así mismo, la ecuación (10) establece que un trabajador ausente recibe una indemnización pública zp y una indemnización complementaria por parte del empleador, zfi; con una probabilidad ψ se recupera de su enfermedad, en cuyo caso ganaría cierto bienestar; finalmente, enfrenta también una probabilidad s de perder su empleo.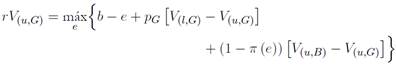
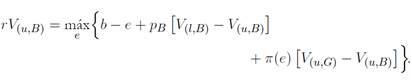
 se vuelve buscador de empleo en el segmento B. Similarmente, la ecuación (12) establece que un desempleado de tipo B recibe una asignación b, encuentra trabajo con una probabilidad
pB
, o con una probabilidad π € orienta su búsqueda de empleo hacia el segmento G.
se vuelve buscador de empleo en el segmento B. Similarmente, la ecuación (12) establece que un desempleado de tipo B recibe una asignación b, encuentra trabajo con una probabilidad
pB
, o con una probabilidad π € orienta su búsqueda de empleo hacia el segmento G.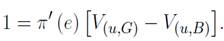
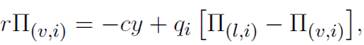
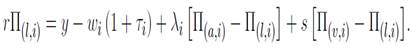
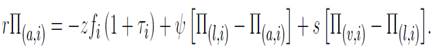
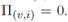 Como no existen barreras a la entrada en el mercado de trabajo, la creación de empleos está dada por la condición de libre entrada Así, mientras exista una renta, se crearán puestos de trabajo en cada segmento del mercado. Al equilibrio, las empresas son entonces indiferentes entre un puesto vacante de tipo G o un puesto vacante de tipo B. Se tiene entonces que:
Como no existen barreras a la entrada en el mercado de trabajo, la creación de empleos está dada por la condición de libre entrada Así, mientras exista una renta, se crearán puestos de trabajo en cada segmento del mercado. Al equilibrio, las empresas son entonces indiferentes entre un puesto vacante de tipo G o un puesto vacante de tipo B. Se tiene entonces que: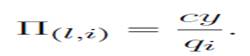
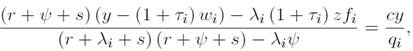
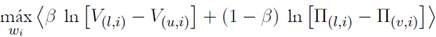



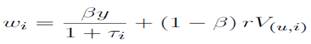
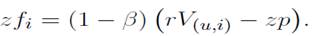
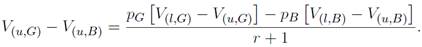
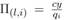 y la expresión del excedente
y la expresión del excedente 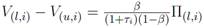 se tiene que:
se tiene que: