Ciclos externos y productos básicos en América Latina y el Caribe: un análisis de cointegración con quiebres
DOI:
https://doi.org/10.17533/udea.le.n88a02Palabras clave:
sector externo, quiebres estructurales, cointegración, América LatinaResumen
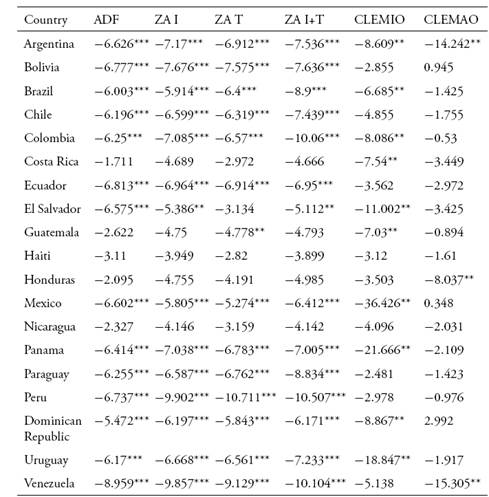
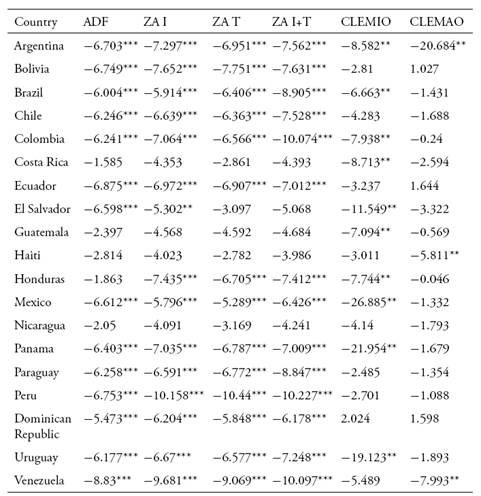
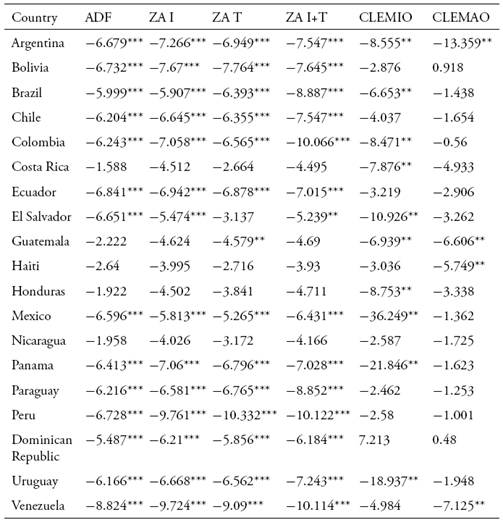
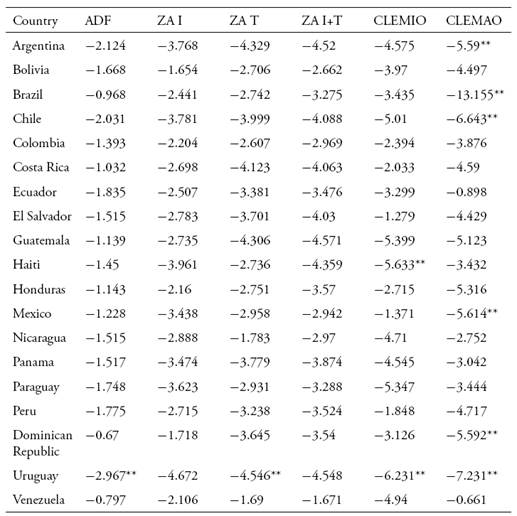
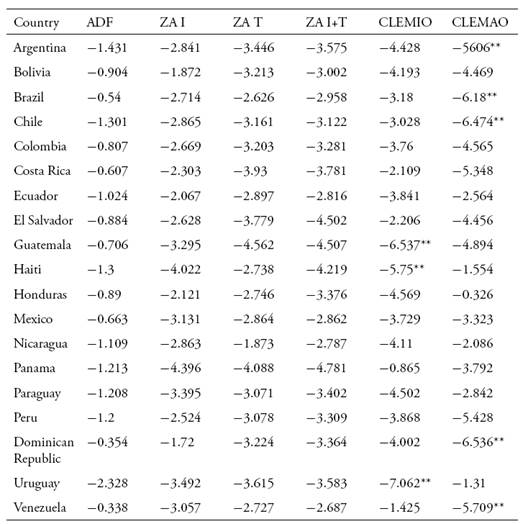
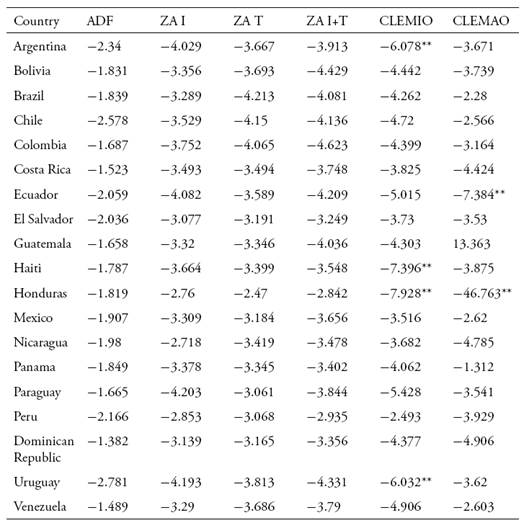
En este trabajo se busca caracterizar la relación entre los comportamientos cíclicos de la cuenta corriente y los índices de precios de los productos básicos (commodities) para América Latina y el Caribe. Usando diferentes test de estacionariedad que permiten la presencia de quiebres, se encuentra evidencia de que los precios de los commodities se encuentran cointegrados con las cuentas corrientes de los países de Latinoamérica, lo que sugiere que los planes desarrollistas no generaron la diversificación productiva deseada y que la posición externa de la región todavía depende fuertemente de los productos básicos. Los resultados también apoyan los hallazgos de Delbianco y Fioriti (2014, 2015) que sostienen que la región ha sufrido dos quiebres estructurales en los últimos 60 años, ambos derivados de cambios en los precios de los commodities.
Descargas
Citas
Akpan, Uduak S.; Isihak, Salisu R. & Asongu, Simplice A. (2014). “Determinants of foreign direct investment in fast-growing economies: a study of BRICS and MINT”, AGDI Working Paper, WP/14/002. African Governance and Development Institute.
Albrieu, Ramiro (2012). “La Macroeconomía de los recursos naturales en América Latina”, En: Ramiro, Albrieu; López, Andrés & Rozenwurcel, Guillermo (Coords.) Los recursos naturales como palanca del desarrollo: ¿ficción o realidad? (pp. 105-153). Red Mercosur.
Bordo, Michael David (1980). “The effects of monetary change on relative commodity prices and the role of long-term contracts”, Journal of Political Economy, Vol. 88, No. 6, pp. 1088-1109.
Bouoiyour, Jamal & Selmi, Refk (2014). “Commodity price uncertainty and manufactured exports in Morocco and Tunisia: Some insights from a novel GARCH model”, Economics Bulletin, Vol. 34, No. 1, pp. 220-233.
Carrion-i-Silvestre, Josep L.; Kim, Dukpa & Perron, Pierre (2009). “GLS-based unit root tests with multiple structural breaks under both the null and the alternative hypotheses”, Econometric Theory, Vol. 25, No. 6, pp. 1754-1792.
CEPAL (2009). América Latina y el Caribe: Series históricas de estadísticas económicas, 1950-2008. Retrieved from: https://www.cepal.org/deype/cuaderno37/esp/index.htm
Clemente, Jesús; Montañés, Antonio & Reyes, Marcelo (1998). “Testing for a unit root in variables with a double change in the mean”, Economics Letters, Vol. 59, No. 2, pp. 175-182.
Chow, Gregory C. (1960). “Tests of equality between sets of coefficients in two linear regressions”, Econometrica, Vol. 28, No. 3, pp. 591-605.
Cody, Brian & Mills, Leonard (1991). “The role of commodity prices in formulating monetary policy”, The Review of Economics and Statistics, Vol. 73, No. 2, pp. 358-365.
Cuñado, Juncal; Gil-Alana, Luis Alberiko & Pérez de Gracia, Fernando (2003). “Empirical evidence on real convergence in some OECD countries”, Applied Economics Letters, Vol. 10, No. 3, pp. 173-176.
Cuñado, Juncal (2011). “Structural Breaks and Real Convergence in OPEC Countries”, Journal of Applied Economics, Vol. 14, No. 1, pp. 101–117.
Dabus, Carlos & Delbianco, Fernando (2014). “Non Convergence in Latin America, a structural break approach”, Working paper. Retrieved from: https://www.researchgate.net/publication/321058237_Non_Convergence_in_Latin_America_a_strcutural_break_approach.
Delbianco, Fernando & Fioriti, Andrés (2014). “The impact of commodities indexes in Argentina: A cointegration analysis with breaks”, The Empirical Economics Letters, Vol. 13, No. 11, pp. 1153-1158.
Delbianco, Fernando & Fioriti, Andrés (2015). “Dependence of Latin America external sector on commodity prices. A contemporaneity analysis using a descriptive approach”, Working paper. Retrieved from: https://www.researchgate.net/publication/321058228_Dependence_of_Latin_America_external_sector_on_commodity_prices_A_contemporaneity_analysis_using_a_descriptive_approach
Dickey, David & Fuller, Wayne (1979). “Distribution of the estimators for autoregressive time series with a unit root”, Journal of the American Statistical Association, Vol. 74, No. 366, pp. 427-431.
Duran Lima, José E. & Álvarez, Mariano (2011). “Manual de comercio exterior y política comercial. Nociones básicas, clasificaciones e indicadores de posición y dinamismo”, Colección Documentos de Proyectos, LC/w.430. Comisión Económica para América Latina y el Caribe, CEPAL.
Frenkel, Roberto & Rapetti, Martín (2011). “Fragilidad externa o desindustrialización: ¿Cuál es la principal amenaza para América Latina en la próxima década?”, Serie de la CEPAL, No. 116. División de Desarrollo Económico, CEPAL.
Gallagher, Kevin & Porzecanski, Roberto (2010). The Dragon in the Room: China and the Future of Latin American Industrialization. Palo Alto: Stanford University Press.
Garner, Alan C. (1989). “Commodity prices: Policy target or information variable? A note”, Journal of Money, Credit and Banking, Vol. 21, No. 4, pp. 508-514.
Herrera, Ana María & Pesavento, Elena (2009). “Oil Price Shocks, Systematic Monetary Policy and the ‘Great Moderation”, Macroeconomic Dynamics, Vol. 13, No. 1, pp. 107-137.
Kim, Dukpa & Perron, Pierre (2009). “Unit root tests allowing for a break in the trend function at an unknown time under both the null and alternative hypotheses”, Journal of Econometrics, Vol. 148, No. 1, pp. 1-13.
Liew, Venus Khim-Sen (2004). “Which lag length selection criteria should we employ?”, Economics Bulletin, Vol. 3, No. 33, pp. 1-9.
Lumsdaine, Robin & Papell, David (1997). “Multiple trend breaks and the unit-root hypothesis”, Review of Economics and Statistics, Vol. 79, No. 2, pp. 212-218.
Perron, Pierre & Vogelsang, Timothy (1992). “Nonstationarity and level shifts with an application to purchasing power parity”, Journal of Business & Economic Statistics, Vol. 10, No. 3, pp. 301-320.
Sachs, Jeffrey & Warner, Andrew (2001). “The Curse of Natural Resources”, European Economic Review, Vol. 45, No. 4-6, pp. 827-838.
Sen, Amit (2004). “Are US macroeconomic series difference stationary or trend-break stationary?”, Applied Economics, Vol. 36, No. 18, pp. 2025-2029.
Verheyen, Florian (2010). “Monetary Policy, Commodity Prices and Inflation: Empirical Evidence from the US”, Ruhr Economic Papers, No. 216. Ruhr-Universitat Bochum, Alemania.
Wei, Yanfeng (2013). “Commodity prices, manufactured goods prices and inflation: evidence from Japan”, Economics Bulletin, Vol. 33, No. 2, pp. 986-992.
Zivot, Eric & Andrews, Donald (1992). “Further Evidence on the Great Crash, the Oil-Price Shock and the Unit-Root Hypothesis”, Journal of Business and Economic Statistics, Vol. 10, No. 3, pp. 251-270.
Descargas
Publicado
Cómo citar
Número
Sección
Licencia
Derechos de autor 2017 Fernando Delbianco, Andrés Fioriti

Esta obra está bajo una licencia internacional Creative Commons Atribución-NoComercial-CompartirIgual 4.0.
Este sitio web, por Universidad de Antioquia, está licenciado bajo una Creative Commons Attribution License.
Los autores que publiquen en esta revista aceptan que conservan los derechos de autor y ceden a la revista el derecho de la primera publicación, con el trabajo registrado con una Licencia de Atribución-NoComercial-CompartirIgual de Creative Commons, que permite a terceros utilizar lo publicado siempre que mencionen su autoría y a la publicación original en esta revista.
Los autores pueden realizar acuerdos contractuales independientes y adicionales para la distribución no exclusiva de la versión del trabajo publicada en la revista (por ejemplo, incluirla en un repositorio institucional o publicarla en un libro) siempre que sea con fines no comerciales y se reconozca de manera clara y explícita que el artículo ha sido originalmente publicado en esta revista.
Se permite y recomienda a los autores publicar sus artículos en Internet (por ejemplo, en páginas institucionales o personales), ya que puede conducir a intercambios provechosos y a una mayor difusión y citación de los trabajos publicados.







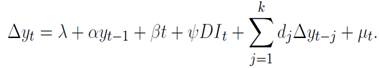
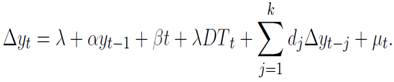
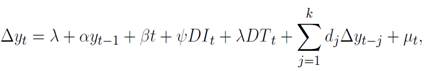
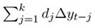 are the lags and
µt
is the error term.
are the lags and
µt
is the error term. 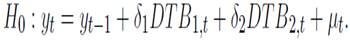
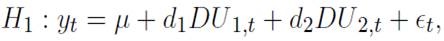
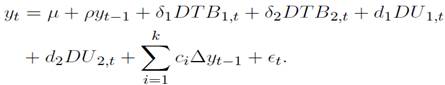
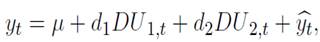
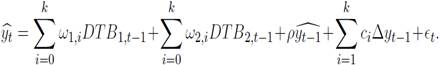
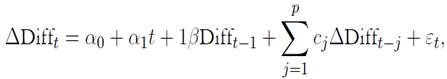
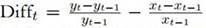 is the difference between the growth rate of y and the growth rate of x, y denotes the price indexes (soybeans, agriculture, metals, energy and non- fuel). The lags are denoted by p, which are included to prevent autocorrelation issues.
is the difference between the growth rate of y and the growth rate of x, y denotes the price indexes (soybeans, agriculture, metals, energy and non- fuel). The lags are denoted by p, which are included to prevent autocorrelation issues.